树形DP2F

T1 树的直径

我们使用\(f[u]\)表示以\(u\)为根的子树，向下延伸的最远距离
那么\(f[u]\)的初始值为0，表示\(u\)能向下延伸的最远距离是自己，\(f[u]=0\)
\(ans=max(ans,f[u]+f[v]+w)ans\)表示直径

错误1

如果有负边权，所以我把\(f[u]\)的初值设置成为一个极小值，这样的话，和\(f[u]\)的意义就背离了，所以不能这样设置，如果有负边权，我们就把\(ans\)的初值设置为极小值就可以了
如果我们把\(f[u]\)设置成极小值，下述的图就会出错，找不到最长的直径为7

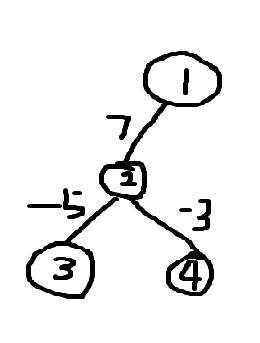
同时，直径指的是树上两点之间的最远距离，如果所有的边权都是负数，那么直径就是所有负边权的最大值

T2 直径的个数

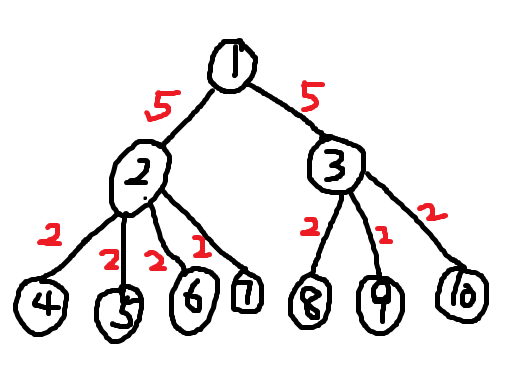
我们先来看这棵树的直径长度是14，共有12个
考虑12个点对从何而来？4和8，9，10，5和8，9，10，依次类推
如果\((u,v)\)构成了直径，那么和\(f[u]\)最远距离相同的点共有多少个，假设有\(num[u]\)个，同理，也有\(num[v]个\),那么直径的个数要加上\(num[u]\)*\(num[v]\),刚开始\(num[u]=1\)，表示距离为0的点有一个，就是自己,其余的部分，和更新最大值是相同的

#include<bits/stdc++.h>
using namespace std;
const int maxn=100005;
int n,zj;
int f[maxn],num[maxn];
long long ans;
vector< pair<int,int> >g[maxn];
void dfs(int u,int fa){num[u]=1;for(auto x:g[u]){int v=x.first;int w=x.second;if(v==fa) continue;dfs(v,u);int dis=f[v]+w;if(dis+f[u]>zj){zj=dis+f[u];ans=num[u]*num[v];}else if(dis+f[u]==zj){ans+=num[u]*num[v];}if(dis>f[u]){num[u]=num[v];f[u]=dis;}else if(dis==f[u])num[u]+=num[v];}
}
int main(){cin>>n;for(int i=1;i<n;i++){int x,y,z;cin>>x>>y>>z;g[x].push_back({y,z});g[y].push_back({x,z});}dfs(1,-1);cout<<zj<<" "<<ans;return 0;
}

T3 Sabota

这个题刚开始的想法是二分答案，假设\(x\)为叛徒的占比，那么我们来看一下以1为根的子树，叛徒的个数会不会超过\(k\)
我们设\(f[u]\)表示以\(u\)为根的子树叛徒的最大数量