数据结构第七章（三）-树形查找：红黑树

---

红黑树

---

红黑树来喽~

我们在上一篇说了二叉排序树（BST）和平衡二叉树（AVL），那么既然都有这两个了，为什么还要发明红黑树？而且红黑树看起来时间复杂度也和平衡二叉树差不多：

	BST	AVL Tree	Red Black Tree
Invention Time	1960	1962	1972
Search	O(n)	O(log2n)	O(log2n)
Insert	O(n)	O(log2n)	O(log2n)
Delete	O(n)	O(log2n)	O(log2n)

我们会发现它俩不是差不多，简直是一毛一样，但是搞出红黑树是有原因的：

平衡二叉树（AVL）：插入/删除 很容易破坏“平衡”特性，需要频繁调整树的形态。如：插入操作导致不平衡，则需要先计算平衡因子，找到最小不平衡子树（时间开销大），再进行 LL/RR/LR/RL 调整

红黑树（RBT）：插入/删除 很多时候不会破坏“红黑”特性，无需频繁调整树的形态。即便需要调整，一般都可以在常数级时间内完成。

所以在实际使用中，平衡二叉树适用于以查为主，很少插入/删除的应用场景；而红黑树适用于频繁插入/删除的场景，实用性更强。

一、红黑树

1.定义

红黑树是二叉排序树，满足 左子树结点值 ≤ 根节点值 ≤ 右子树结点值；

它是二叉排序树，但是它不是普通的二叉排序树。与普通的BST相比，它有如下要求：

1. 每个结点或是红色的，或是黑色的；

2. 根节点是黑色的；

3. 叶结点（外部结点、NULL结点、失败结点）均是黑色的；

4. 不存在两个相邻的红结点（即红结点的父节点和孩子结点均是黑色）；

5. 对每个结点，从该节点到任一叶结点的简单路径上，所含黑结点的数目相同。

注意，我们在红黑树中说的“叶结点”并不是叶子结点了，而是叶子结点的下一层，也就是查找失败的位置的结点。

那么它的结点结构就该这么定义：

struct RBNode{          //红黑树的结点定义int key;            //关键字的值RBNode* parent;     //双亲结点指针RBNode* lchild;     //左孩子指针RBNode* rchild;     //右孩子指针int color;          //结点颜色，如：可用0/1表示黑/红，也可以使用枚举型enum表示颜色
};

有个color表示结点是红色还是黑的，这和平衡二叉树中有个balance表示该结点的平衡因子异曲同工；但是这里还有一个指向双亲结点的指针，证明我们可能需要找到双亲的操作会比较多，所以直接在结构体内定义会比较方便。

上面那些红黑树的要求是什么意思呢？第一是说，这结点必须得有颜色，要么红要么黑；第二是说，如果它是一棵红黑树，那么它的根节点必是黑色的；第三是说，失败结点是黑色的（别急，马上看个图就知道了）；第四是说，从上往下捋，不能有俩红结点挨着；第五是说，每个结点无论到那个叶结点的路径中，经过的黑结点数目都相同。

话不多说，上图：

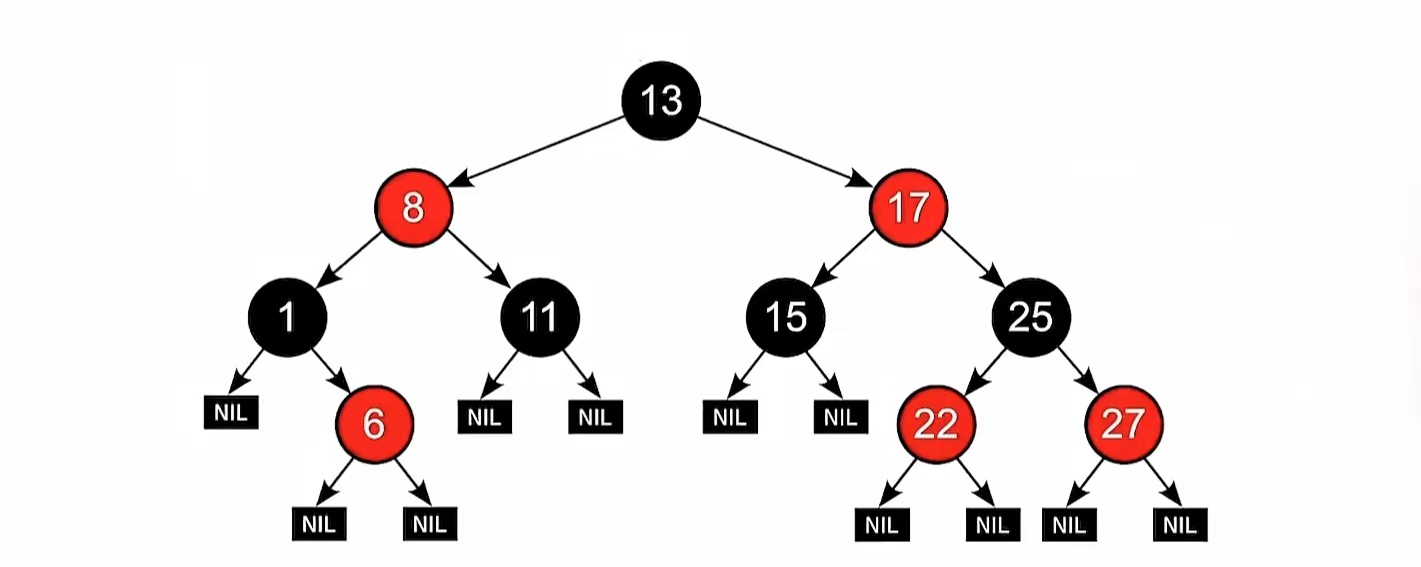
我们看到这个图，就能很明显地明白红黑树里面的“叶结点”（失败结点）是什么意思了，就是方的那个“NULL”，也被叫做“外部结点”。

且我们可以看到，对每个结点，从该节点到任一叶结点的简单路径上，所含黑结点的数目相同。比如这个图中的根节点，它到任一叶结点所含的黑结点的数目都是2，再比如“17”结点，它到任一叶结点所含的黑结点的数目都是1，而且这个图中也没有两个相邻的红结点，这是一棵水灵灵的红黑树。

红黑树的定义那么多，这怎么记得住……不过道高一尺，魔高一丈，我们有个口诀，直接一下概括刚刚说的红黑树的所有定义，它就是——

左根右，根叶黑，不红红，黑路同

先别管它中二不中二，问题不大，好用就行。

这也很好理解，“左根右”是它二叉排序树的特性，“根叶黑”是指根结点、叶结点的颜色都是黑的，“不红红”是指不存在两个相邻的红结点，“黑路同”是指对每个结点，从该节点到任一叶结点的简单路径上，所含黑结点的数目相同，简单易懂，朗朗上口，奈斯~

那么我们刚刚看到了一棵活的红黑树，现在我们来看看不符合红黑树要求的是啥样的：

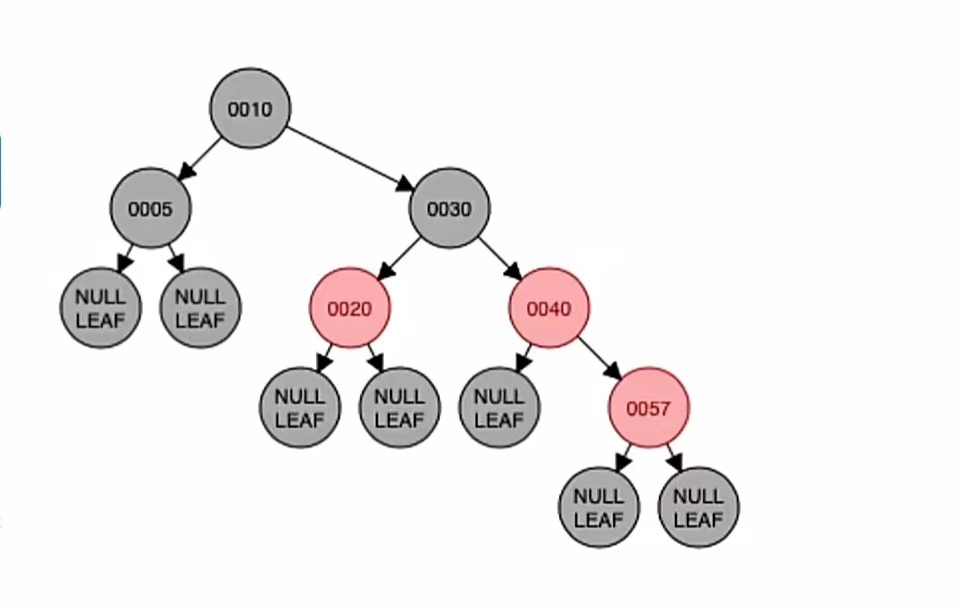
这个一看就知道，它不满足“不红红”，有两个红的相邻了，所以不是红黑树；

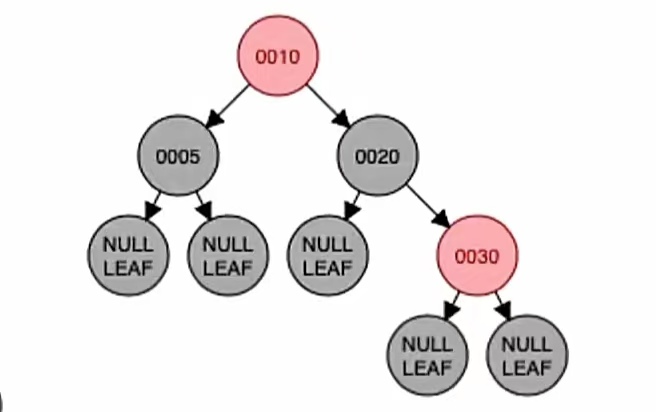
这个违反了什么？违反了“根叶黑”呀，它的根是红色的不是黑色的，所以也不是红黑树；

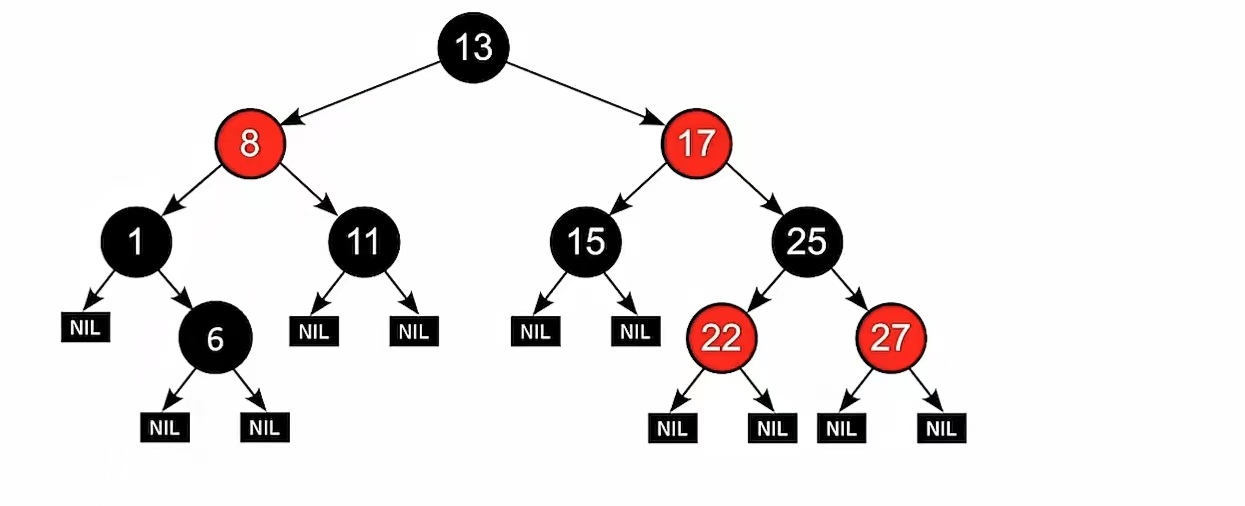
这个违反了什么？藏得比较深，它违反了“根路同”。你看它从结点“8”去任一叶结点， “8——1——NULL” 经过的黑色结点是2个，但是“8——1——6——NULL”经过的黑色结点是3个，所以也不是红黑树；

但是如果这个结点“6”变成红色，那就满足红黑树的定义，它就变成红黑树了。

当然！！！要注意会不会给你挖坑，比如让你判断是不是红黑树，它倒是颜色没什么毛病，但你不能此时就觉得它是红黑树了啊喂！！！还要注意它是不是满足二叉排序树“左≤根≤右”的要求，有些题就特别阴险，这么对你，所以还是要细心，要多留意一下记得。

2.黑高

什么是“黑高”？我们来看一张图：

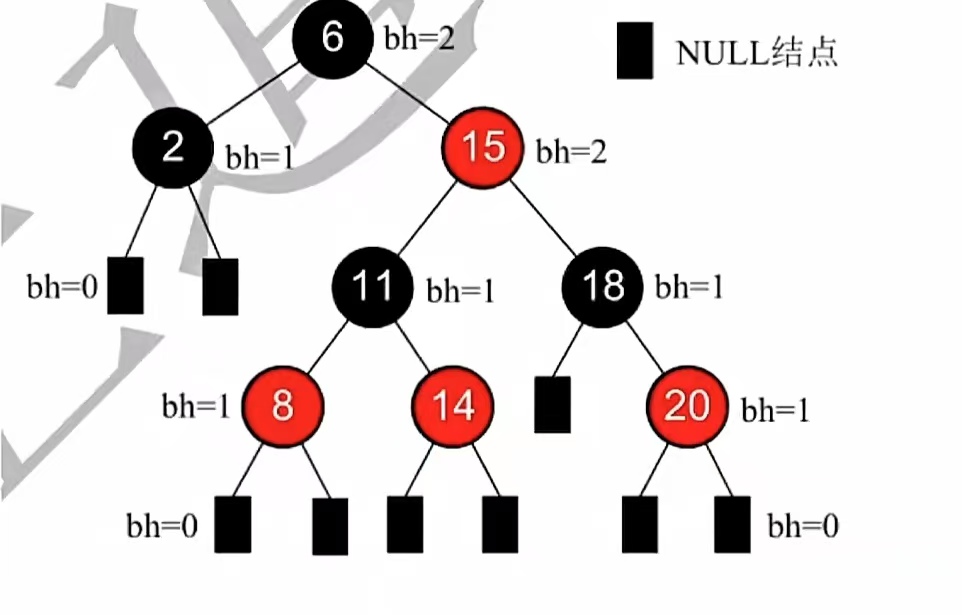
这里面标的bh就是“黑高”。

红黑树结点的黑高 bh ——从某结点出发（不含该节点）到达任一空叶结点的路径上黑结点总数

其实也就是“黑路同”中的“黑路”，这能让我们更加直观比较看看黑路同不同。

这就引申出一个问题：

根节点黑高为h的红黑树，内部结点数（关键字）至少有多少个？

注意，此处的“内部结点”说法对应于把失败结点称为“外部结点”，简单来说“内部结点”就是我们这些红黑树图里圆形的结点，“外部结点”就是我们这些红黑树图里方形的NULL结点。

那么我们内部结点最少是什么情况？既要满足红黑树定义“左根右，根叶黑，不红红，黑路同”，又要内部结点最少，所以最少情况不就是全都是黑的嘛？又因为要“黑路同”，所以就应该是一棵满二叉树。

举个栗子，比如bh=2，根节点黑高为2的内部结点最少情况应该是这样的：

so

内部结点数最少的情况——总共h层黑结点的满树形态

又因为h层一共有2^h-1 个结点，所以 若根结点黑高为h，内部结点数（关键字）最少有2^h-1 个。

3.性质

现在我们已经知道了红黑树是什么，那么由红黑树的定义可以得出红黑树的性质：

1. 从根节点到叶结点的最长路径不大于最短路径的2倍
2. 有n个内部节点的红黑树高度 h ≤ 2log₂(n+1)

性质1是为什么呢？因为我们的“不红红”。最短就是没有红的，最长就是两个黑的中间夹一个红的，所以最长路径不大于最短路径的2倍；

性质2我们刚刚说黑高的时候说了，若根结点黑高为h，内部结点数（关键字）最少有2^h-1 个

还有，若红黑树总高度 = h，则根节点黑高 ≥ h/2。因为根节点的黑高（从根到叶子的路径上黑色结点数）至少是树总高度h的一半，要么占完，要么插一些红结点，至少是一半。

so因为红黑树总高度 = h，根节点黑高 ≥ h/2，又因为若根结点黑高为h，内部结点数（关键字）最少有2^h-1 个，所以内部结点数 n ≥ 2^h/2 - 1 ，由此推出 h ≤ 2log₂(n+1)。

由性质2可知，红黑树查找操作时间复杂度为 O(log₂n)，查找效率与AVL树同等数量级。

红黑树的查找与ASL相同，从根出发，左小右大，若查找到一个空叶结点，则查找失败。

二、插入

还记得我们平衡二叉树的插入吗？插入后要先看平不平衡，不平衡要通过旋转调整成平衡，其实万变不离其宗，我们红黑树也是。插入后要看有没有破坏红黑树的定义，破坏了也要调整，调整到还是一棵红黑树，这就是插入完成。

1.插入步骤

• 先查找，确定插入位置（原理同二叉排序树），插入新结点
• 新结点是 根——染为黑色
• 新结点 非根——染为红色
  • 若插入新结点后依然满足红黑树定义，则插入结束
  • 若插入新结点后不满足红黑树定义，需要调整，使其重新满足红黑树定义
    • 黑叔：旋转+染色
      • LL型：右单旋，父换爷+染色
      • RR型：左单旋，父换爷+染色
      • LR型：左、右双旋，儿换爷+染色
      • RL型：右、左双旋，儿换爷+染色
    • 红叔：染色+变新
      • 叔父爷染色，爷变为新结点

2.举例

我们来看一个栗子，方便我们更好地理解

从一棵空的红黑树开始，插入： 20， 10， 5， 30， 40， 57， 3， 2， 4， 35， 25， 18， 22， 23， 24， 19， 18

首先是插入结点“20”，那么由上面的红黑树插入步骤可知，当插入的新结点为根时，染成黑色，所以现在的红黑树是这个样子的：

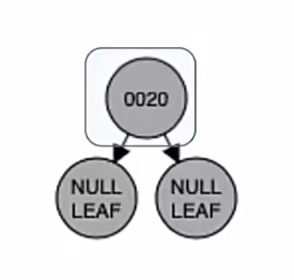
此时我们要判断插入新结点后满不满足红黑树定义，发现是满足我们那个口诀的，所以插入完成。

接下来插入的是结点“10”，根据二叉排序树那样插入，应该插到“20”的左子树上；而由上面的红黑树插入步骤我们也知道，当插入的新结点非根时，染成红色，就是这样：

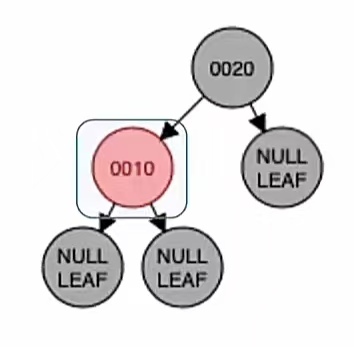
此时我们要判断插入新结点后满不满足红黑树定义，发现是满足我们那个口诀的（左根右，根叶黑，不红红，黑路同），所以插入完成。

其实哈，我们后面判断满不满足红黑树的性质，只要看满不满足“不红红”就行了。为啥咧？因为我们插入是按照二叉排序树插入方法，所以不会破坏“左根右”；新结点不是根的话，也不会破坏“根叶黑”；新结点不是根就给染成红色，红色是不会增加“黑路同”的；所以就一个“不红红”容易被破坏，so我们按照上面的红黑树插入步骤插入的时候判断满不满足红黑树定义，这是一个快捷的办法。

下面插入的是结点“5”，根据二叉排序树那样插入，应该插到“10”的左子树上；而由上面的红黑树插入步骤我们也知道，当插入的新结点非根时，染成红色，就是这样：

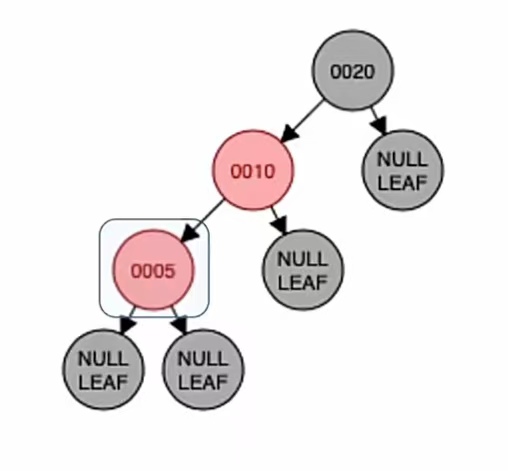
显然，我们插入新结点后不满足红黑树定义，需要调整，使其重新满足红黑树定义。怎么调整？要按照双亲的兄弟结点的颜色来，也就是看叔结点的颜色进行不同的步骤来调整，就是上面说的这样：

• 若插入新结点后不满足红黑树定义，需要调整，使其重新满足红黑树定义
  • 黑叔：旋转+染色
    • LL型：右单旋，父换爷+染色
    • RR型：左单旋，父换爷+染色
    • LR型：左、右双旋，儿换爷+染色
    • RL型：右、左双旋，儿换爷+染色
  • 红叔：染色+变新
    • 叔父爷染色，爷变为新结点

显然我们新结点“5”有一个“黑叔”（NULL）（弱弱说以及……现在大概能理解为啥要把失败结点也当做红黑树的一部分并且染黑了，因为方便找“叔”和观察“叔”的颜色），那么有“黑叔”，我们应该先旋转再变色。

旋转：

看新结点是“LL”型，所以我们应该进行右单旋，由上一篇我们知道，右单旋是转“儿子”，所以也就是这样：

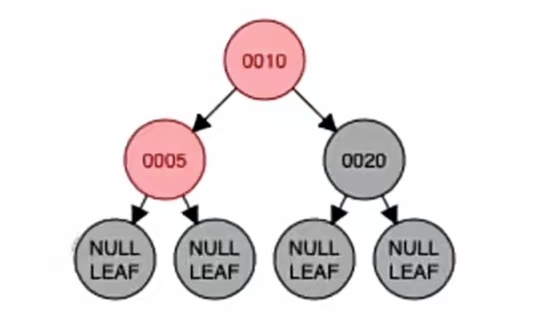
染色：

我们转的是“儿子”，所以把“儿子”和“爷”染色（注意，这里说的“儿子”是相对于插入新结点的爷结点说的，“爷”是相对于插入的新结点说的），也就是结点“10”和结点“20”染色，就是下面这样，我们调整完成：

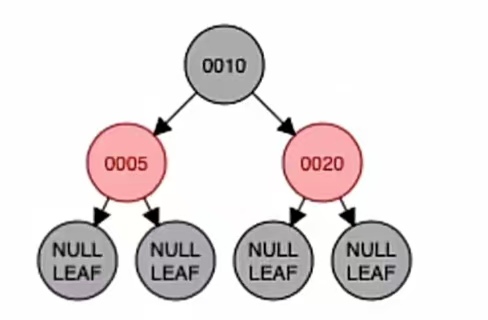
接下来插入的是结点“30”，根据二叉排序树那样插入，应该插到“20”的右子树上；而由上面的红黑树插入步骤我们也知道，当插入的新结点非根时，染成红色，就是这样：

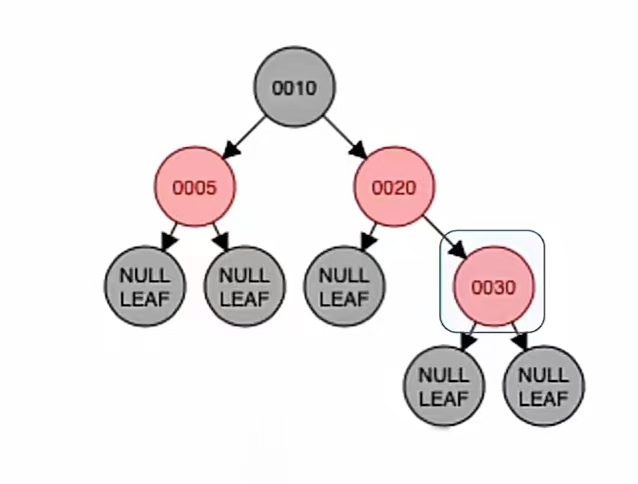
也可以显然看到，这个违反了“不红红”，所以插入新结点后不满足红黑树定义，需要调整，使其重新满足红黑树定义，还是要按照叔的颜色来，也就还是这样：

• 若插入新结点后不满足红黑树定义，需要调整，使其重新满足红黑树定义
  • 黑叔：旋转+染色
    • LL型：右单旋，父换爷+染色
    • RR型：左单旋，父换爷+染色
    • LR型：左、右双旋，儿换爷+染色
    • RL型：右、左双旋，儿换爷+染色
  • 红叔：染色+变新
    • 叔父爷染色，爷变为新结点

可以看到我们新结点“30”有一个“红叔”结点“5”，有“红叔”，我们应该染色+变新。

染色：

把新节点的“叔父爷”进行染色，也就是基于自身换个颜色，黑变红红变黑，也就是下面这样：

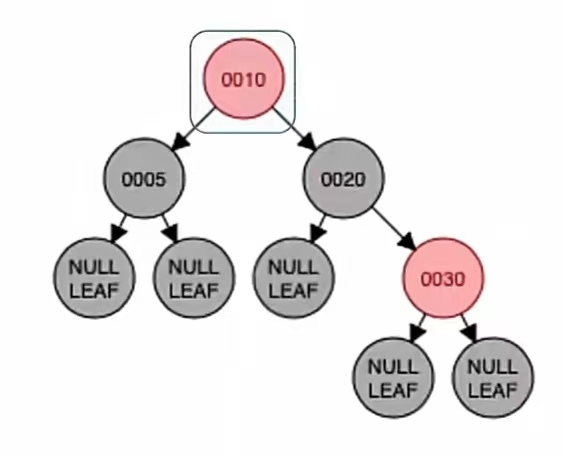
变新：

变新是指爷结点变为新结点，也就是把爷结点当做新插入的结点。那么我们新插入一个结点，首先要干什么？判断它是不是根是吧，显然这个是根，新结点是根我们就要染成黑色，所以就是这个样子滴：

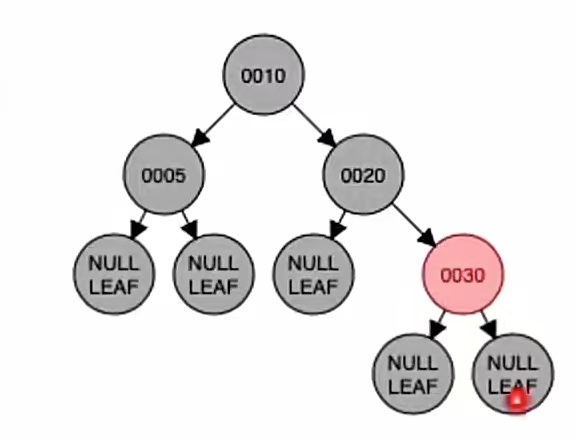
只有插入红色才会违反“不红红”，新结点染黑那就不会违反“不红红”，所以插入新结点后依然满足红黑树定义，插入结束。

然后插入的是结点“40”，根据二叉排序树那样插入，应该插到“30”的右子树上；而由上面的红黑树插入步骤我们也知道，当插入的新结点非根时，染成红色，就是这样：

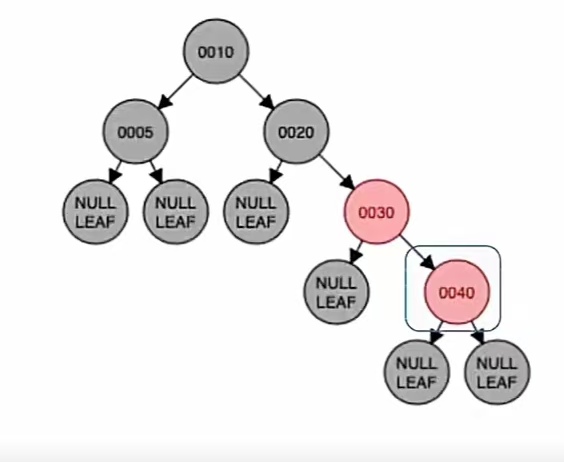
显然违反了“不红红”，我们还是要进行调整，调整看它叔的颜色。它的叔为“黑叔”NULL，所以我们应该“旋转+染色”。

旋转：

新结点是RR型，所以我们进行左单旋，也就是这样：

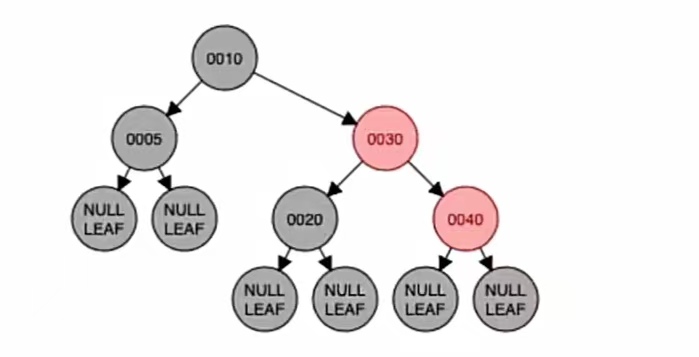
染色：

RR型左单旋，转的是最小不平衡子树的根节点的儿子（也就是新节点的“父”）；新结点的“父”、“爷”染色，也就是“30”和“20”染色，这样：

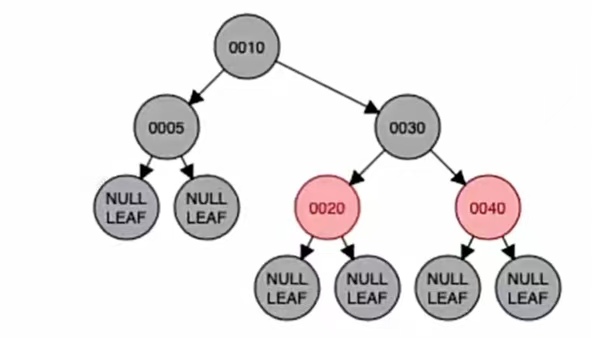
调整完成。

下面插入新结点“57”，根据二叉排序树那样插入，应该插到“40”的右子树上；而由上面的红黑树插入步骤我们也知道，当插入的新结点非根时，染成红色，就是这样：

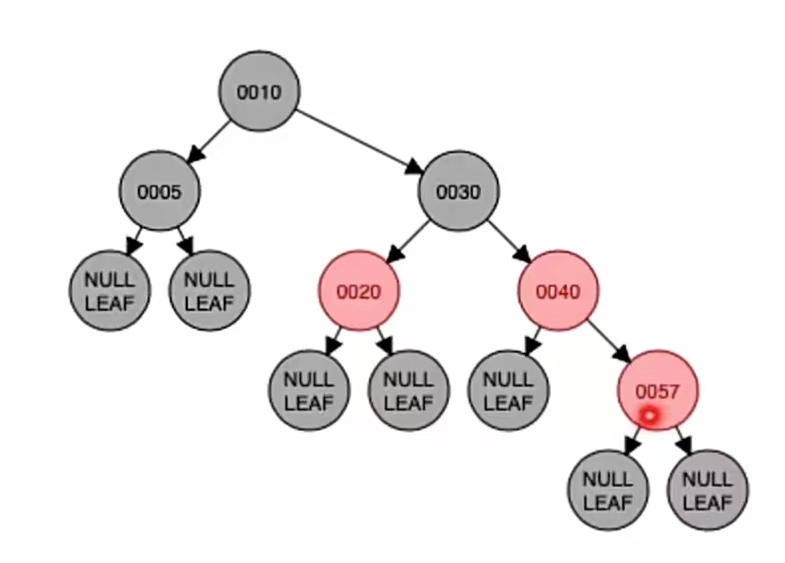
显然违反了“不红红”，我们还是要进行调整，调整看它叔的颜色。它的叔为“红叔”结点“20”，所以我们应该“染色+变新”。

染色：

新节点的叔父爷染色，黑变红红变黑，也就是结点“20”，“40”，“30”变色，就是这样：

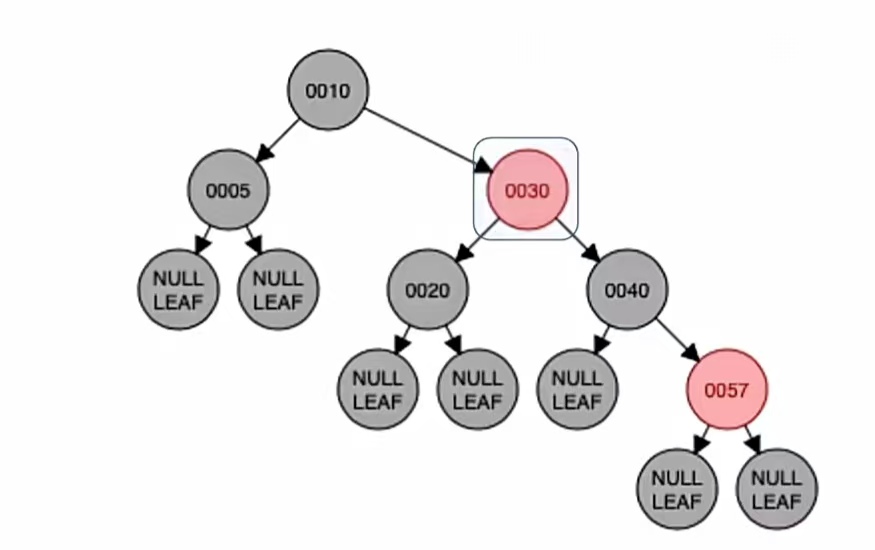
变新：

变新是指爷结点变为新结点，也就是把爷结点当做新插入的结点。那么我们新插入一个结点，首先要干什么？判断它是不是根是吧，显然这个不是根，新结点非根我们就要染成红色，它本来就是红色的，变成红色也不违反“不红红”，所以我们调整完成。

之后插入新结点“3”，根据二叉排序树那样插入，应该插到“5”的左子树上；而由上面的红黑树插入步骤我们也知道，当插入的新结点非根时，染成红色，就是这样：

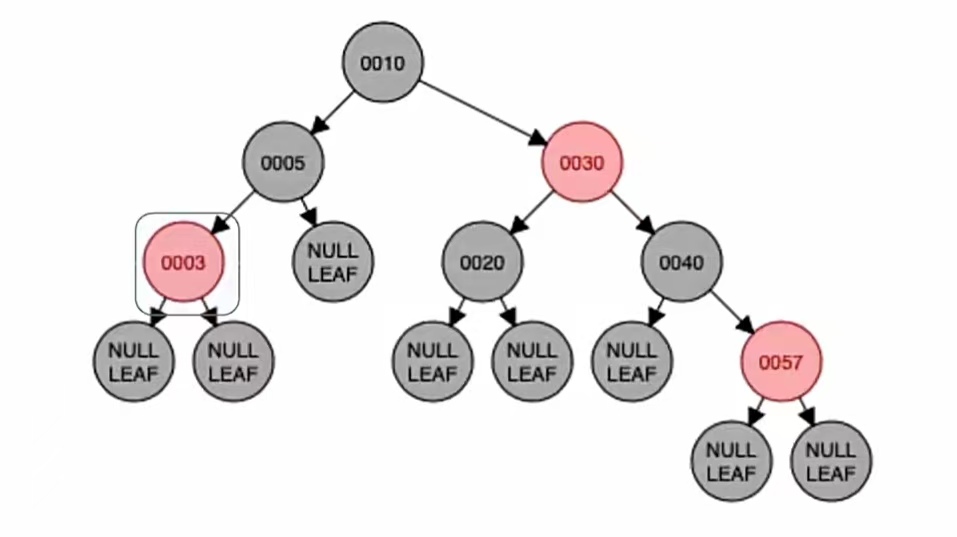
可以看到，插入新结点后不违反“不红红”。插入新结点后依然满足红黑树定义，所以我们插入结束。

然后插入新结点“2”，根据二叉排序树那样插入，应该插到“3”的左子树上；而由上面的红黑树插入步骤我们也知道，当插入的新结点非根时，染成红色，就是这样：

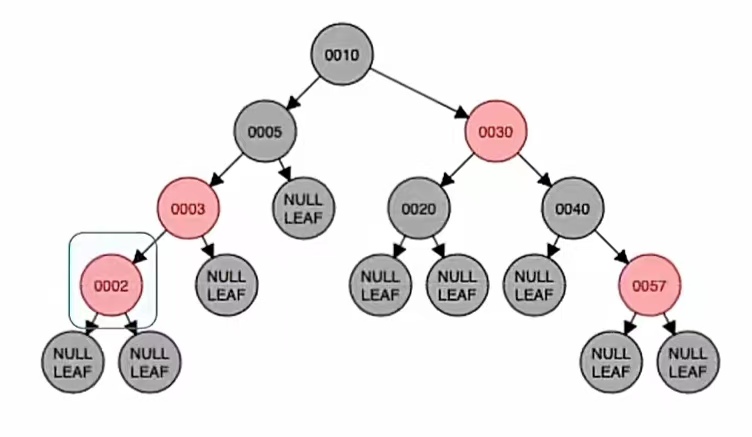
显然违反了“不红红”，我们还是要进行调整，调整看它叔的颜色。它的叔为“黑叔”结点NULL，所以我们应该“旋转+染色”。

旋转：

新结点为LL型，应该进行右单旋，即：

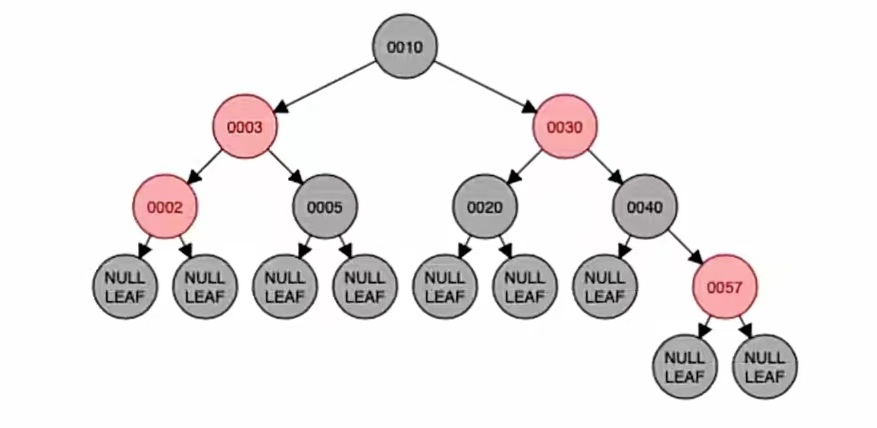
染色：

LL型右单旋，转的是最小不平衡子树的根节点的儿子（也就是新节点的“父”）；新结点的“父”、“爷”染色，也就是“3”和“5”染色，红变黑黑变红，就是这个样子：

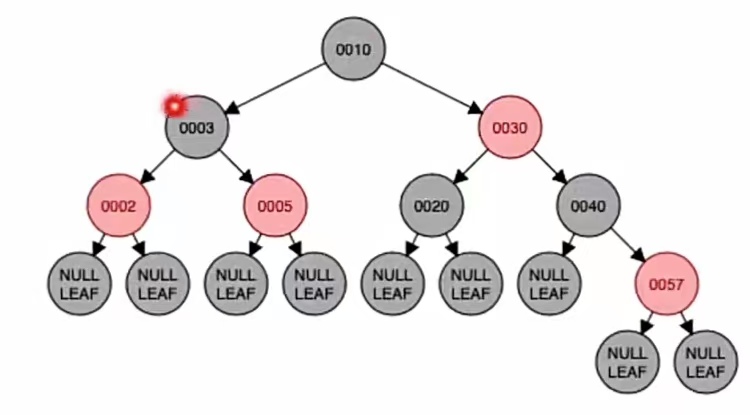
调整完成。

(好多啊……怎么那么多结点……

我们再插入新结点“4”，根据二叉排序树那样插入，应该插到“5”的左子树上；而由上面的红黑树插入步骤我们也知道，当插入的新结点非根时，染成红色，就是这样：

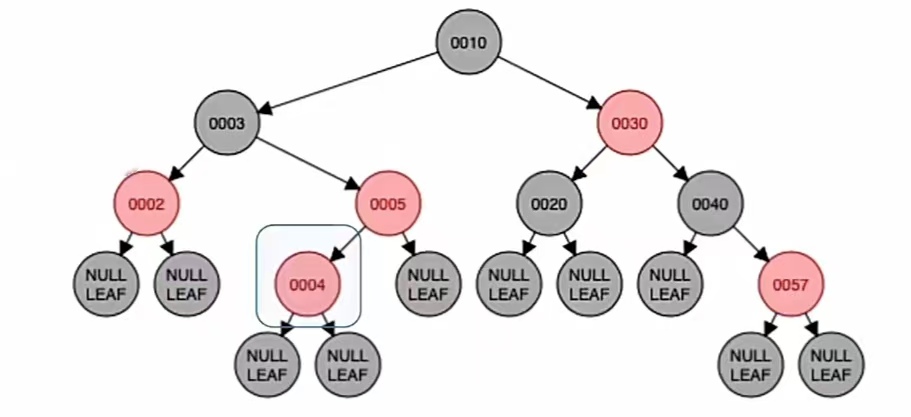
显然违反了“不红红”，我们还是要进行调整，调整看它叔的颜色。它的叔为“红叔”结点“2”，所以我们应该“染色+变新”。

染色：

新节点的叔父爷染色，黑变红红变黑，也就是结点“2”，“5”，“3”变色，就是这样：

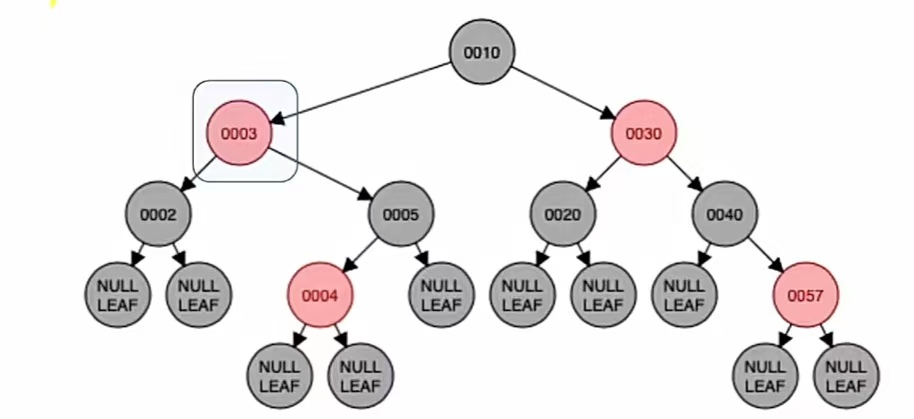
变新：

变新是指爷结点变为新结点，也就是把爷结点当做新插入的结点。那么我们新插入一个结点，首先要干什么？判断它是不是根是吧，显然这个不是根，新结点非根我们就要染成红色，它本来就是红色的，变成红色也不违反“不红红”，所以我们调整完成。

然后我们插入新结点“35”，根据二叉排序树那样插入，应该插到“40”的左子树上；而由上面的红黑树插入步骤我们也知道，当插入的新结点非根时，染成红色，就是这样：

可以看到，插入新结点后不违反“不红红”。插入新结点后依然满足红黑树定义，所以我们插入结束。

我们再插入新结点“25”，根据二叉排序树那样插入，应该插到“20”的右子树上；而由上面的红黑树插入步骤我们也知道，当插入的新结点非根时，染成红色，就是这样：

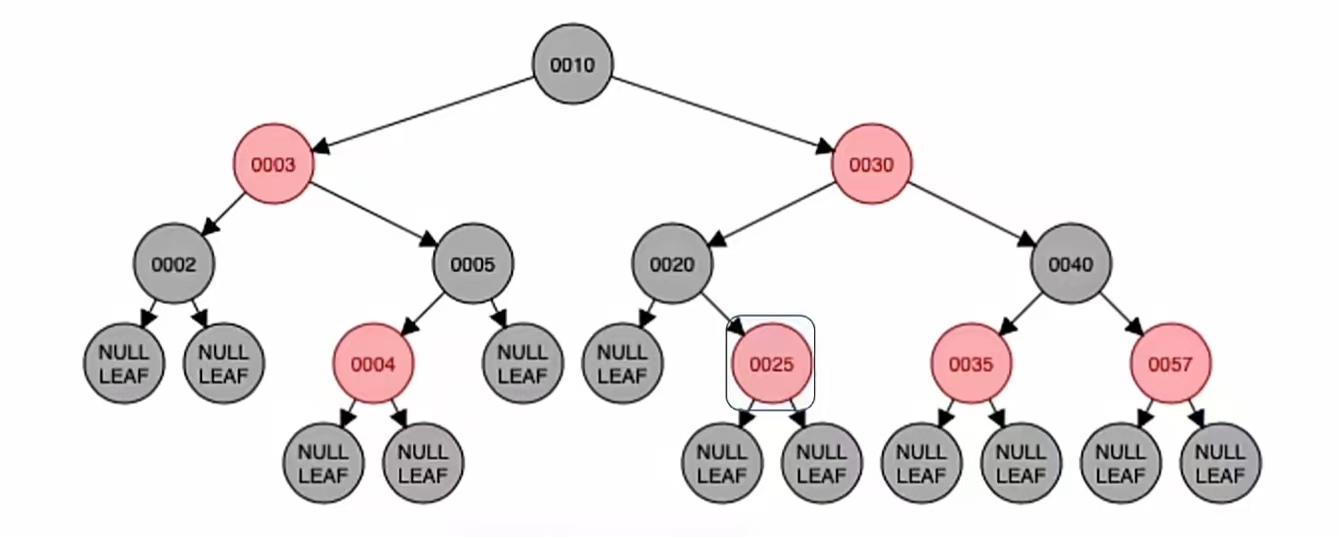
可以看到，插入新结点后不违反“不红红”。插入新结点后依然满足红黑树定义，所以我们插入结束。

性能逐渐优秀……

我们再再插入新结点“18”，根据二叉排序树那样插入，应该插到“20”的左子树上；而由上面的红黑树插入步骤我们也知道，当插入的新结点非根时，染成红色，就是这样：

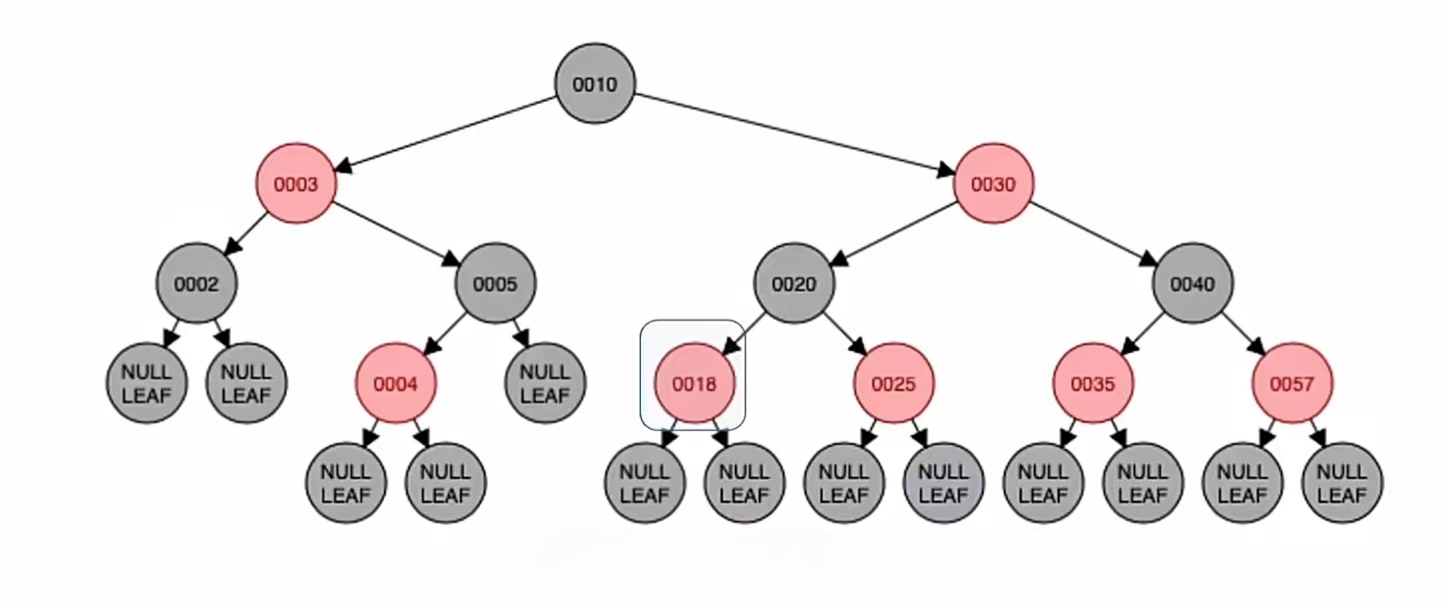
可以看到，插入新结点后不违反“不红红”。插入新结点后依然满足红黑树定义，所以我们插入结束。

然后我们再插入新结点“22”，根据二叉排序树那样插入，应该插到“25”的左子树上；而由上面的红黑树插入步骤我们也知道，当插入的新结点非根时，染成红色，就是这样：

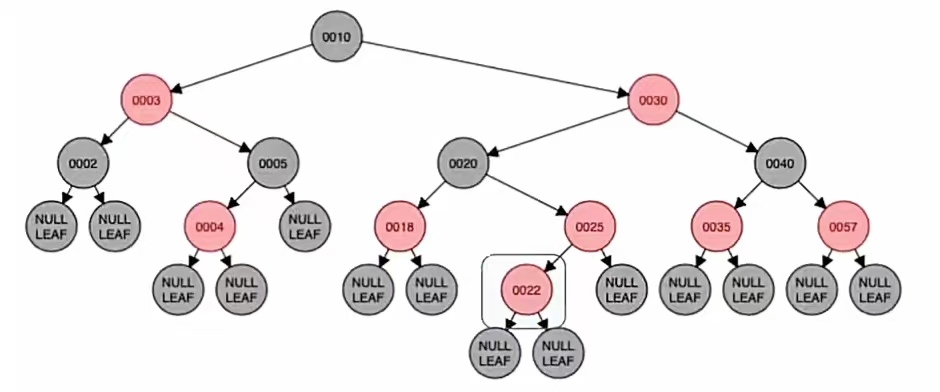
显然违反了“不红红”，我们还是要进行调整，调整看它叔的颜色。它的叔为“红叔”结点“18”，所以我们应该“染色+变新”。

染色：

新节点的叔父爷染色，黑变红红变黑，也就是结点“18”，“25”，“20”变色，就是这样：

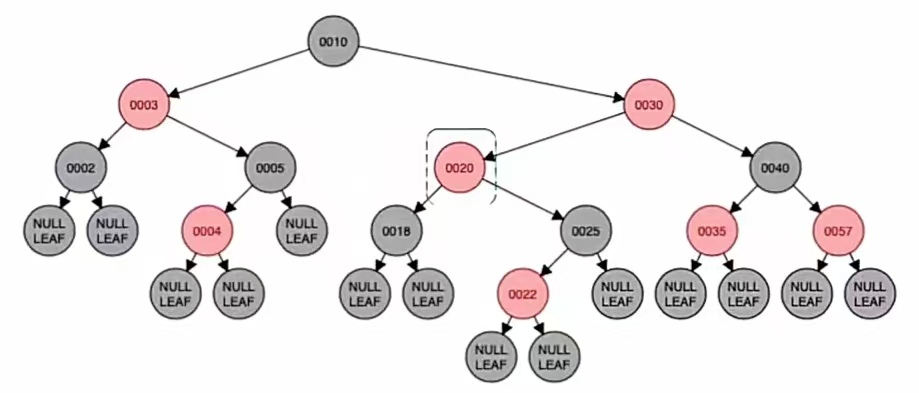
变新：

变新是指爷结点变为新结点，也就是把爷结点当做新插入的结点。那么我们新插入一个结点，首先要干什么？判断它是不是根是吧，显然这个不是根，新结点非根我们就要染成红色，它本来就是红色的。

但是！！！变成红色违反了“不红红”，所以我们应该进行调整。调整看它叔的颜色，它的叔为“红叔”结点“3”，所以我们应该“染色+变新”。

染色：

新节点的叔父爷染色，黑变红红变黑，也就是结点“3”，“30”，“10”变色，就是这样：

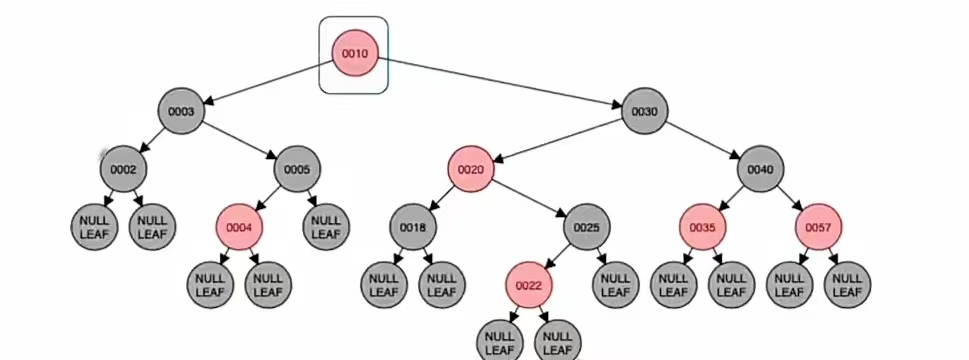
变新：

变新是指爷结点变为新结点，也就是把爷结点当做新插入的结点。那么我们新插入一个结点，首先要干什么？判断它是不是根是吧，显然这个是根，新结点是根我们就要染成黑色，所以把爷结点（现在的新结点）“10”染成黑色，就是这样：

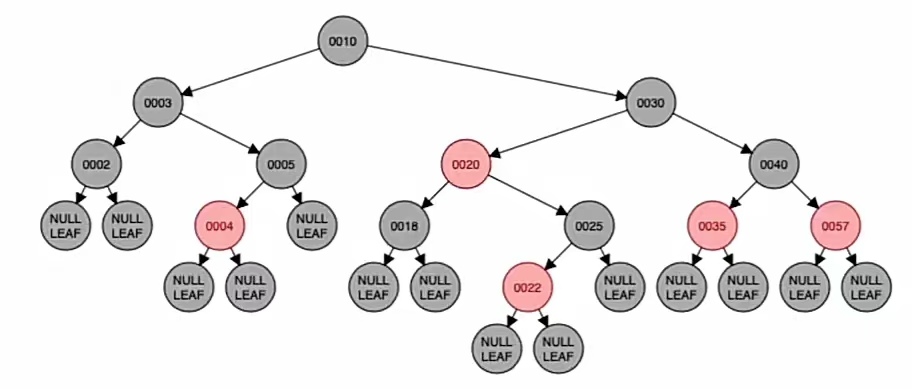
只有插入红色才会违反“不红红”，新结点染黑那就不会违反“不红红”，所以插入新结点后依然满足红黑树定义，插入结束。

下面我们插入新结点“23”，根据二叉排序树那样插入，应该插到“22”的右子树上；而由上面的红黑树插入步骤我们也知道，当插入的新结点非根时，染成红色，就是这样：

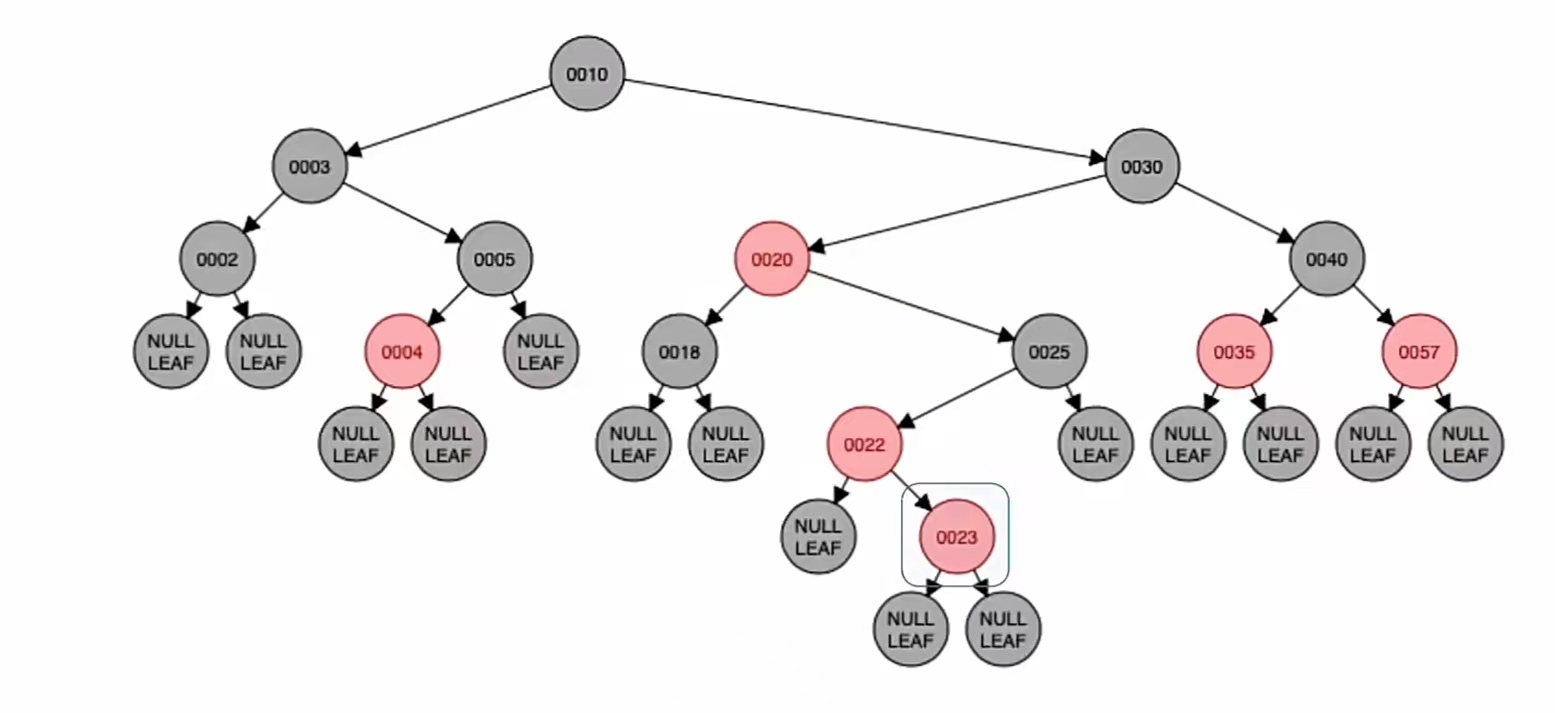
显然违反了“不红红”，我们还是要进行调整，调整看它叔的颜色。它的叔为“黑叔”结点NULL，所以我们应该“旋转+染色”。

旋转：

新结点为LR型，应该对新结点先进行左旋，再进行右旋，即

左旋：

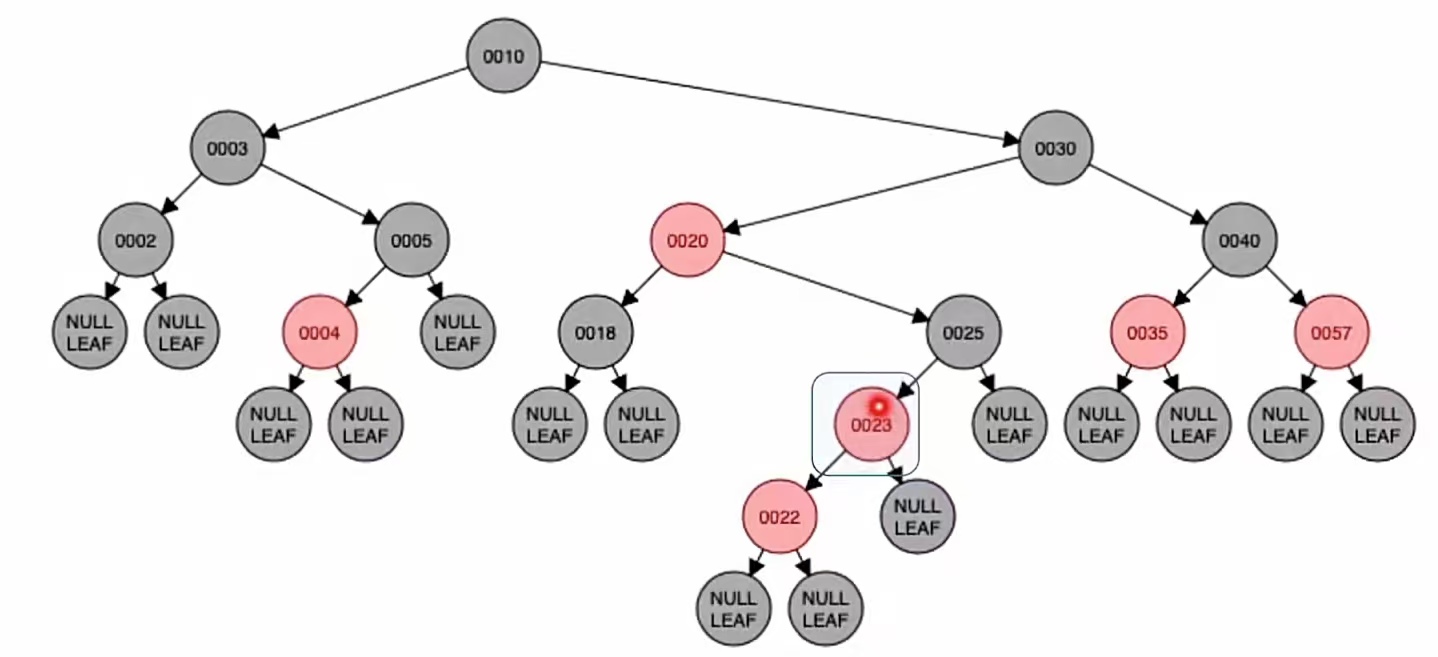
右旋：

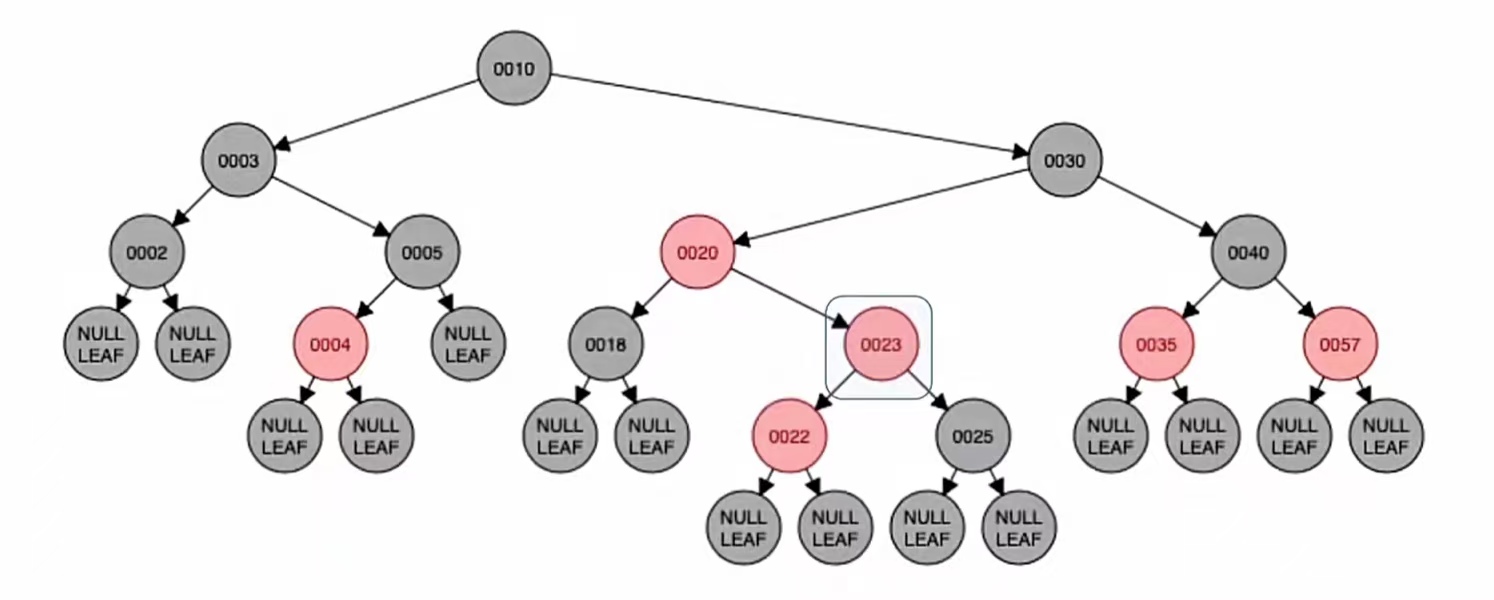
染色：

LR型先左旋再右旋，转的是最小不平衡子树的根节点的孙子（也就是新节点）；新结点和“爷”染色，也就是“23”和“25”染色，红变黑黑变红，就是这个样子：

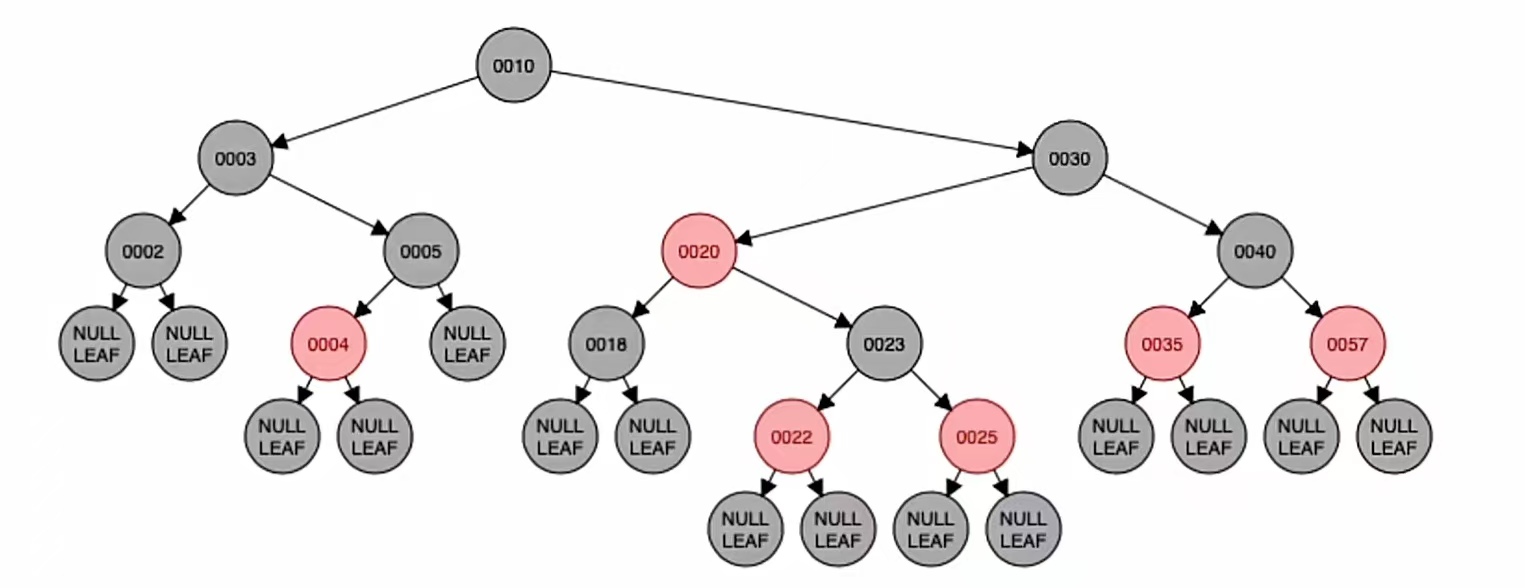
调整完成。

然后我们再插入新结点“24”，根据二叉排序树那样插入，应该插到“25”的左子树上；而由上面的红黑树插入步骤我们也知道，当插入的新结点非根时，染成红色，就是这样：

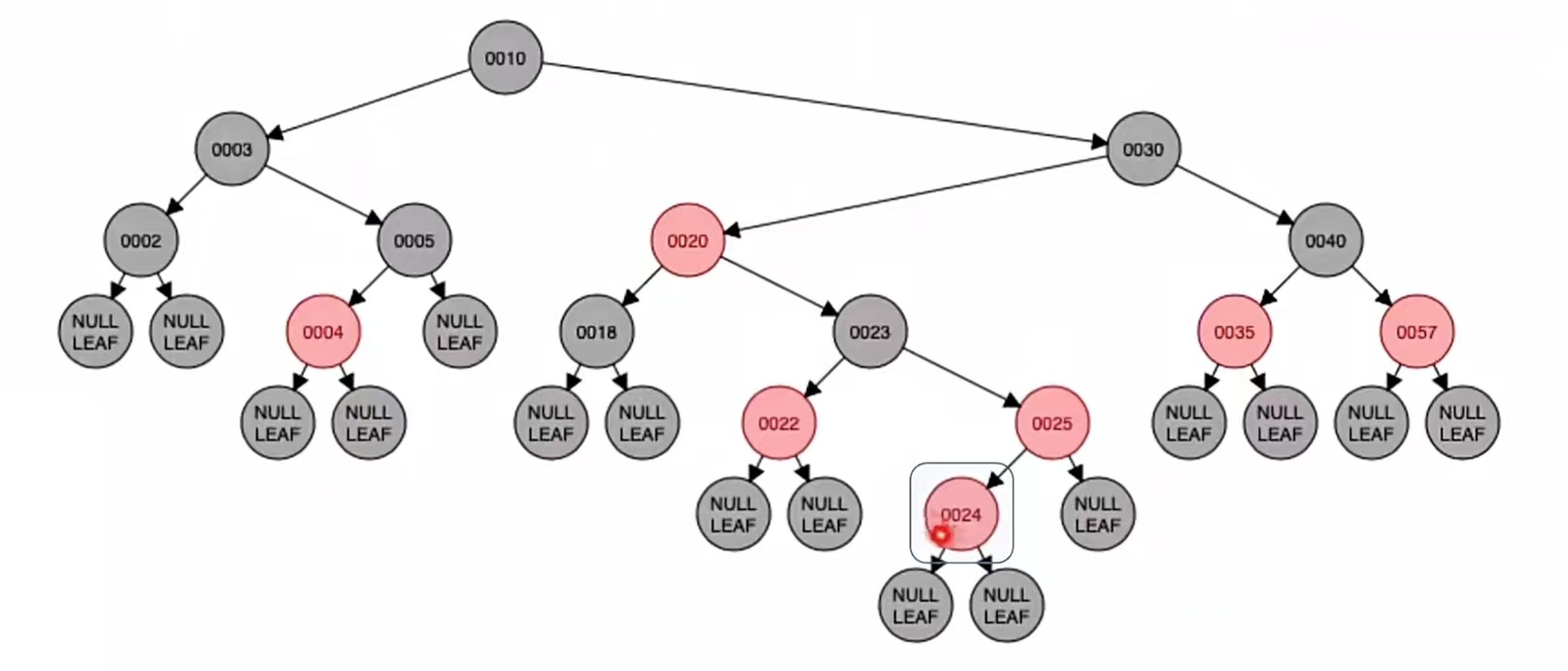
显然违反了“不红红”，我们还是要进行调整，调整看它叔的颜色。它的叔为“红叔”结点“22”，所以我们应该“染色+变新”。

染色：

新节点的叔父爷染色，黑变红红变黑，也就是结点“22”，“25”，“23”变色，就是这样：

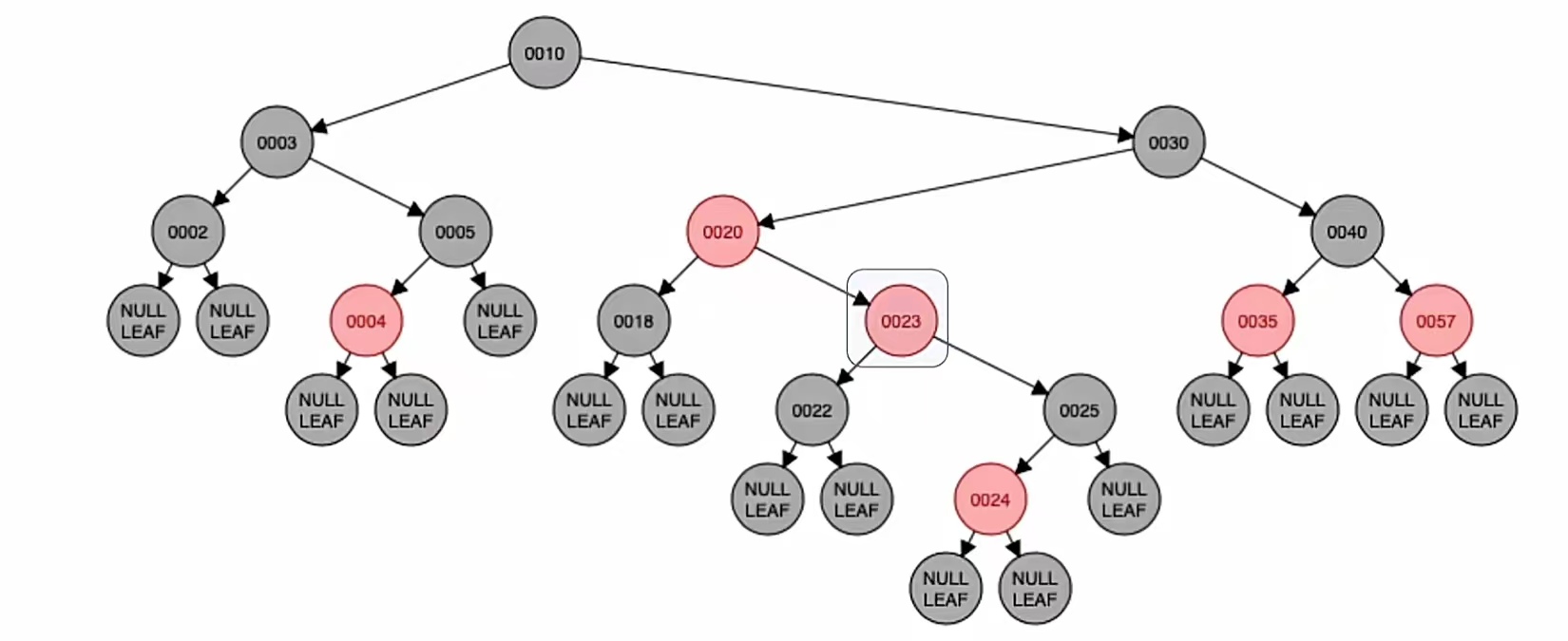
变新：

变新是指爷结点变为新结点，也就是把爷结点当做新插入的结点。那么我们新插入一个结点，首先要干什么？判断它是不是根是吧，显然这个不是根，新结点非根我们就要染成红色，它本来就是红色的。

但是！！！变成红色违反了“不红红”，所以我们应该进行调整。调整看它叔的颜色，它的叔为“黑叔”结点“40”，所以我们应该“旋转+染色”。

旋转：

新结点为LR型，应该对新结点先进行左旋，再进行右旋，即

左旋：

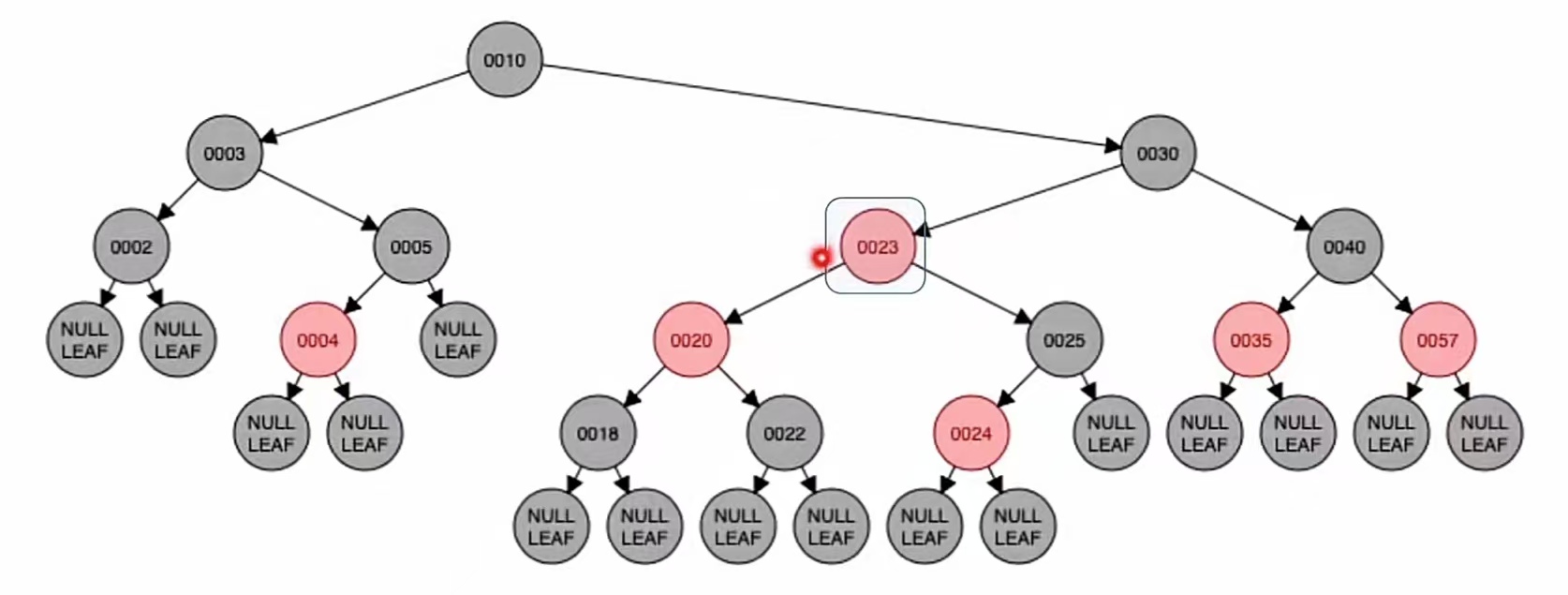
右旋：

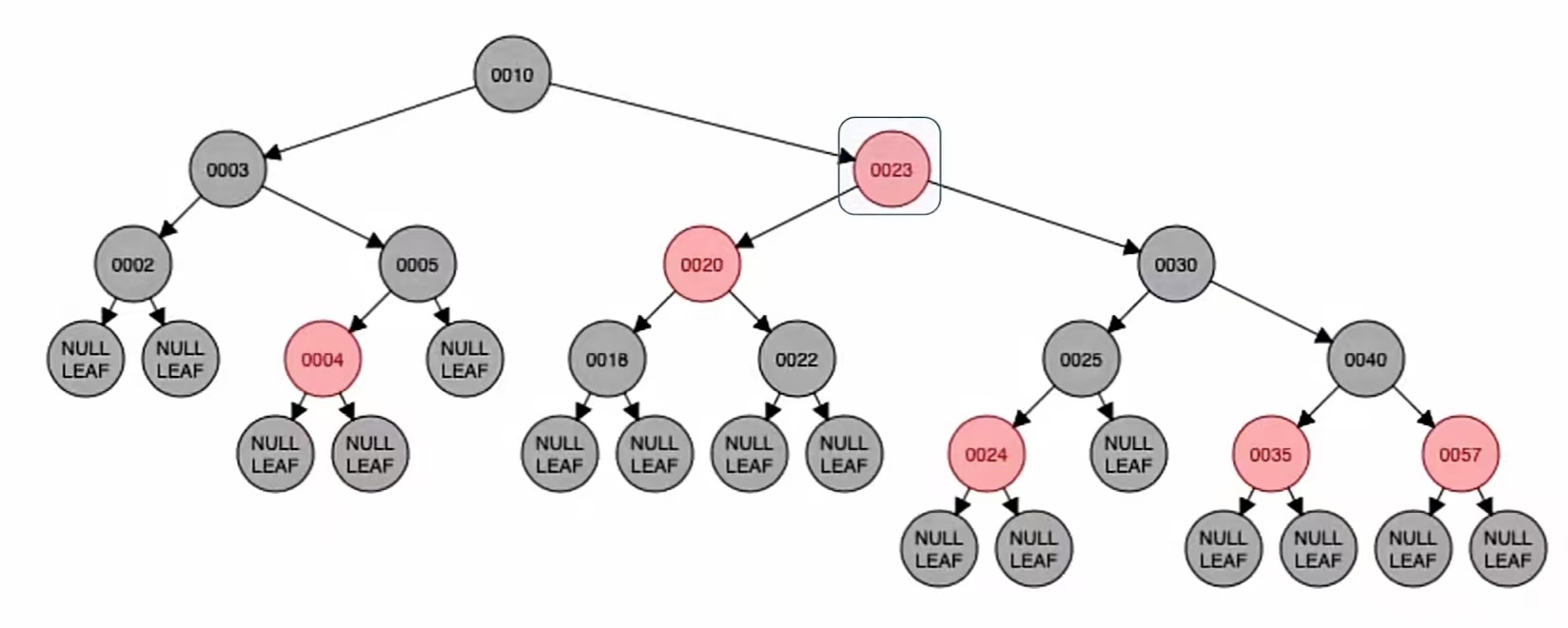
染色：

LR型先左旋再右旋，转的是最小不平衡子树的根节点的孙子（也就是新节点）；新结点和“爷”染色，也就是“23”和“30”染色，红变黑黑变红，就是这个样子：

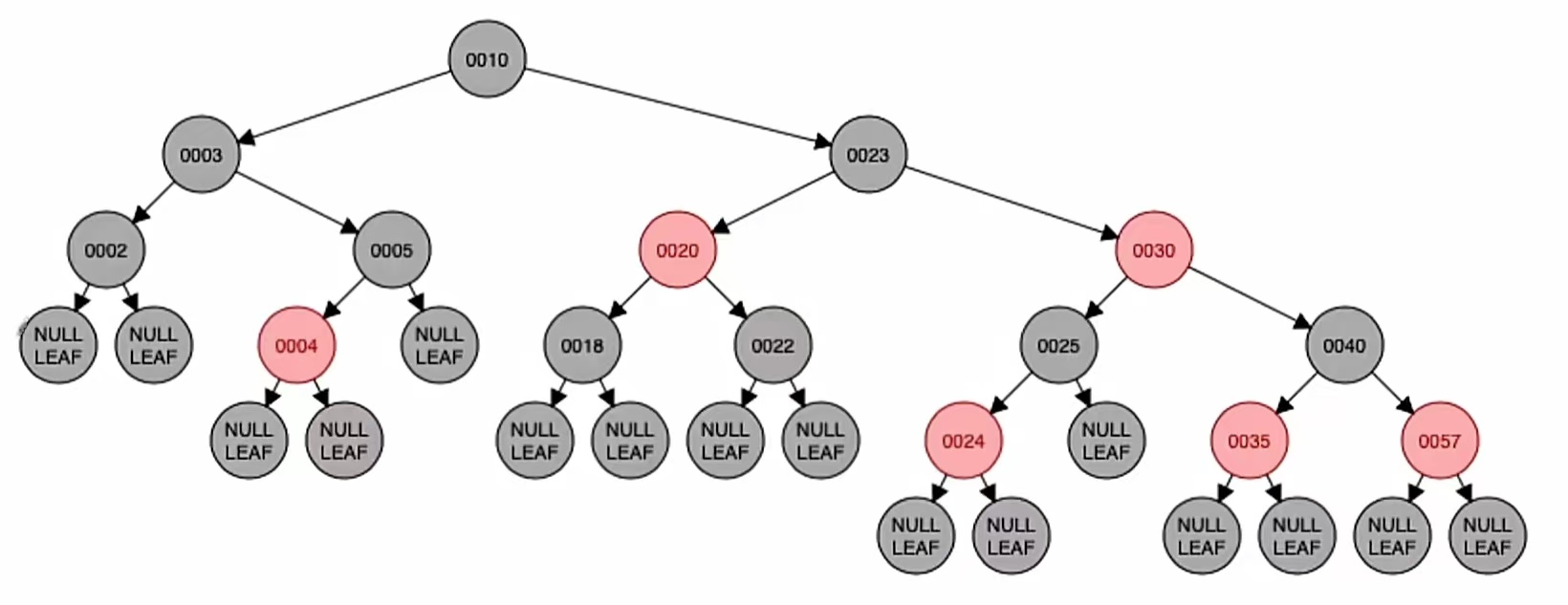
调整完成。

然后我们再插入新结点“19”，根据二叉排序树那样插入，应该插到“18”的右子树上；而由上面的红黑树插入步骤我们也知道，当插入的新结点非根时，染成红色，就是这样：

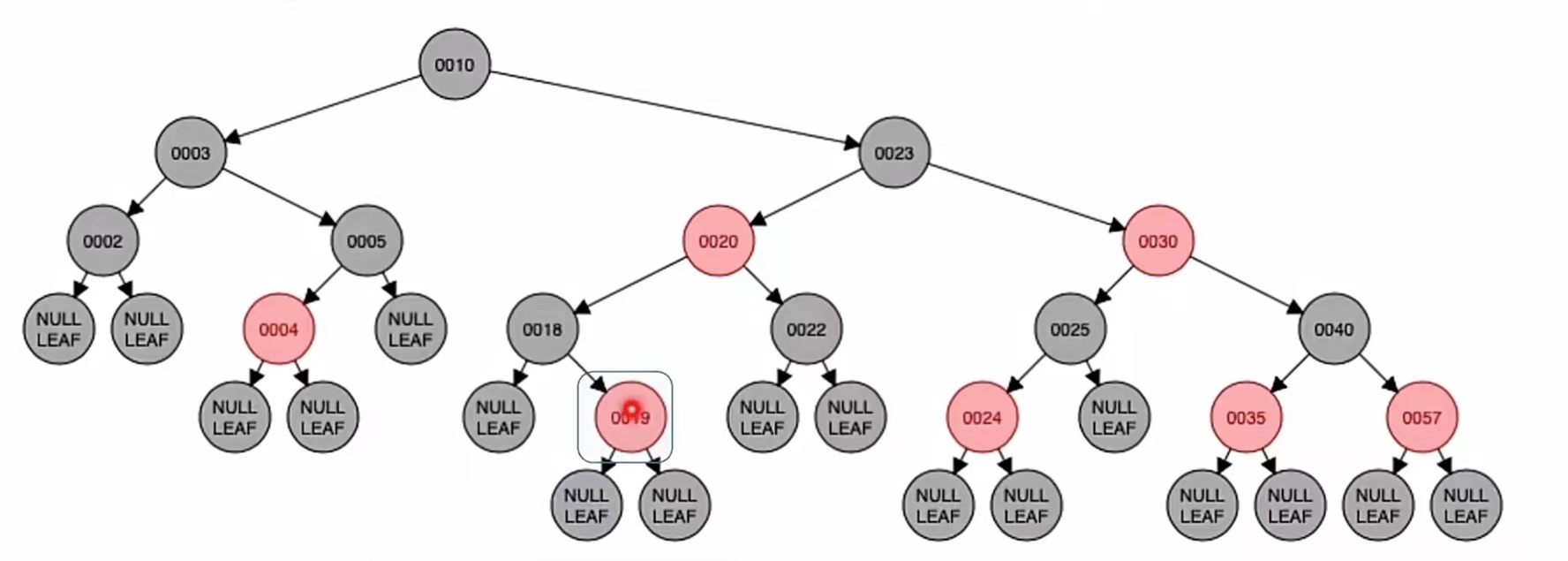
可以看到，插入新结点后不违反“不红红”。插入新结点后依然满足红黑树定义，所以我们插入结束。

最后一个结点！！！胜利就在前方！

我们最后插入新结点“18”，根据二叉排序树那样插入。这个是根据我们的应用场景来的，因为我们的红黑树里已经有“18”了，所以我们可以放在右边也可以放在左边，也可以看到里面有了就不插了，比较灵活不是死的。

那么我们现在给它放到原“18”结点的右子树里，也就是插到“19”的左子树上；而由上面的红黑树插入步骤我们也知道，当插入的新结点非根时，染成红色，就是这样：

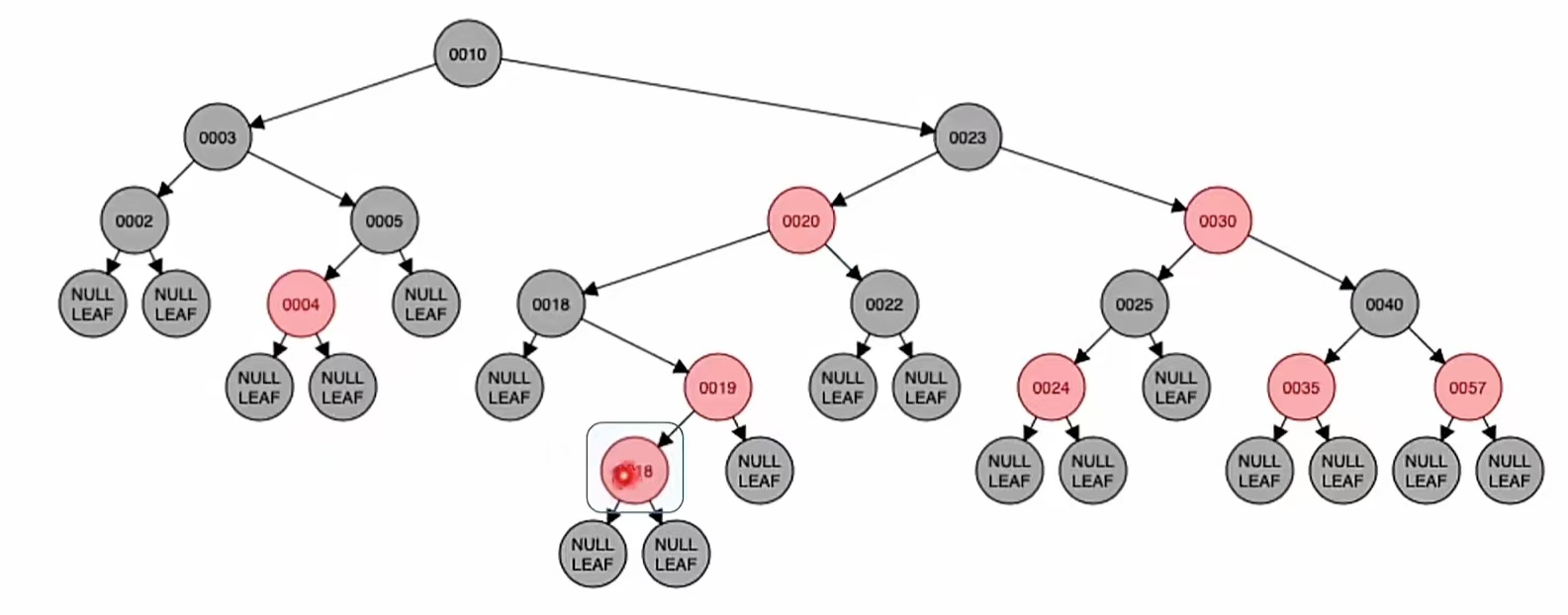
显然违反了“不红红”，我们还是要进行调整，调整看它叔的颜色。它的叔为“黑叔”结点NULL，所以我们应该“旋转+染色”。

旋转：

新结点为RL型，应该对新结点先进行右旋，再进行左旋，即

右旋：

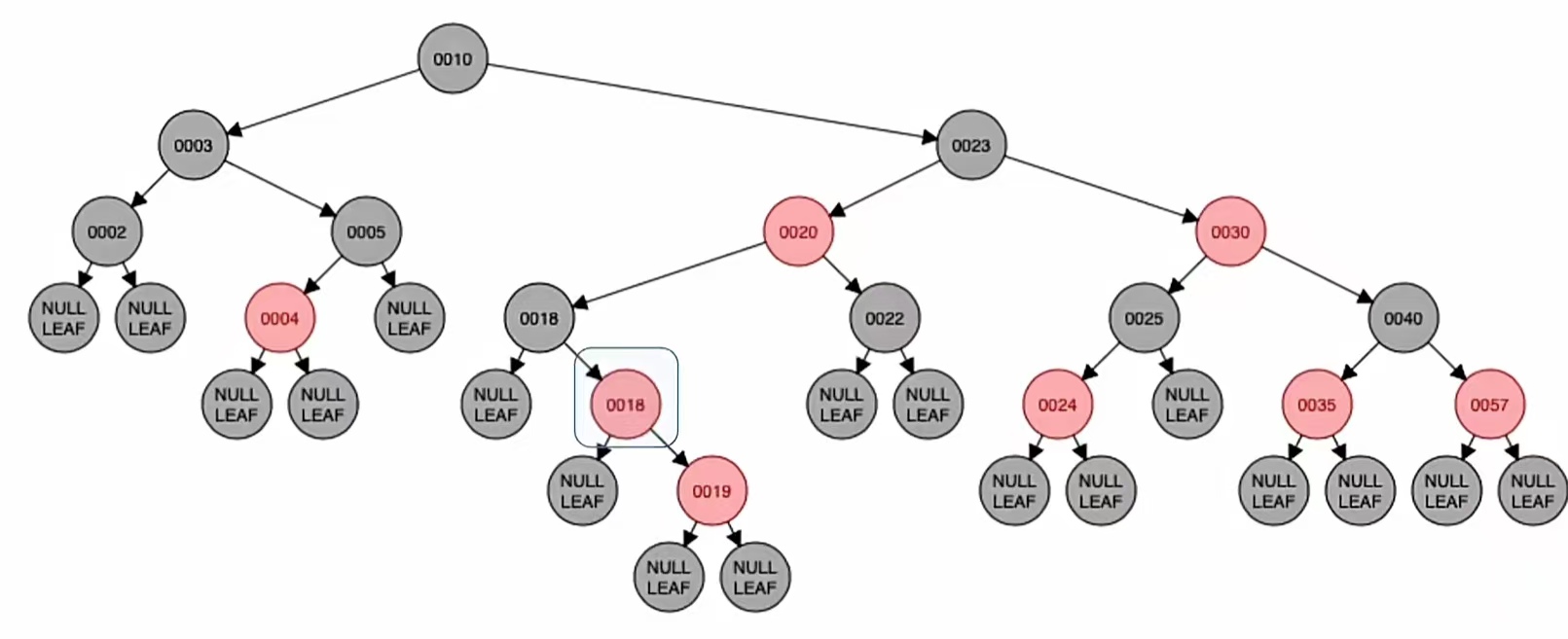
然后再进行左旋。

旋转后要进行染色：

RL型先右旋再左旋，转的是最小不平衡子树的根节点的孙子（也就是新节点）；新结点和“爷”染色，也就是“18”和“18”染色，红变黑黑变红，就是这个样子：

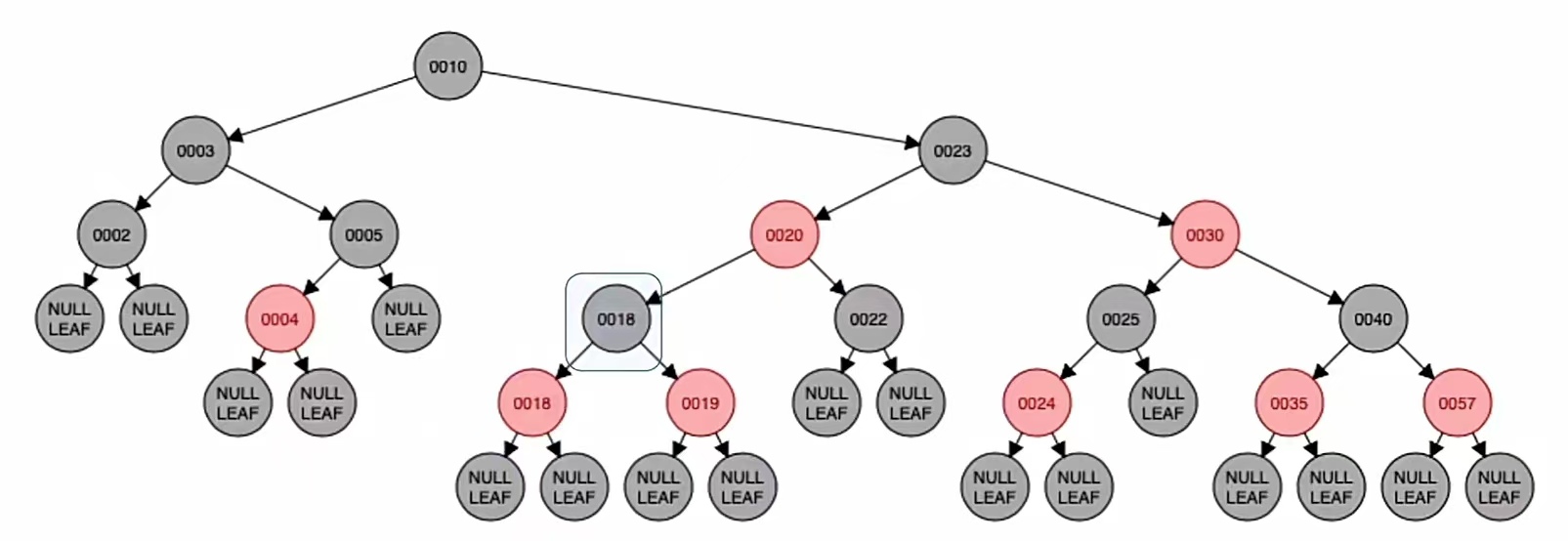
于是我们调整完成。

啊~终于完成了，其实这样就能明显了解红黑树的插入到底是怎么回事了，确实是很麻烦，步骤要搞清楚，要注意的细节比较多。

有一个网站，这个网站上可以自己动态模拟一下刚刚红黑树的插入过程，记得勾上“Show Null Leaves”显示空叶结点，还有可以点击“pause”进行暂停查看，使用“Step Forward/Step Back”进行单步演示。

321上链接~

https://www.cs.usfca.edu/~galles/visualization/RedBlack.html

---

总结

就是红黑树的插入特别复杂，情况判断有点多。先看插入的是不是根，是就黑不是就红，完了要是不满足红黑树定义就看叔的颜色，黑叔就“旋转+染色”，红叔就“染色+变新”，黑叔的染色是看你怎么转，LL、RR就是染最小不平衡子树的根和儿子，LR、RL就是染最小不平衡子树的根和孙子，红叔的染色就是新节点的叔父爷染色，完了爷结点再变为新结点，就是这样了，其他也没啥。