当前位置：首页 > news >正文

数据结构（七）——图

news 来源：原创 2025/7/5 7:15:14

一、图的定义与基本术语

1.图的定义

图G由顶点集V和边集E组成，记为G=(V,E)，其中V(G)表示图G中顶点的有限非空集；E(G)表示图G中顶点之间的关系（边）的集合

注意：线性表可以是空表，树可以是空树，图不可以是空图，图可以没有边，但是至少要有一个顶点。

2.图的基本术语

（1）有向图：若E是有向边(简称弧)的有限集合时，则G为有向图。弧是顶点的有序对，记为<vw>，其中v，w是顶点。当v 是弧尾，w 是弧头时，称为从顶点v到顶点w的弧。

（2）无向图：若E是无向边(简称边)的有限集合时，则G为无向图。边是顶点的无序对，记为(v,w)或(w,v)，且有(v,w)=(w,v)。其中 v，w 是顶点。

（3）完全图：

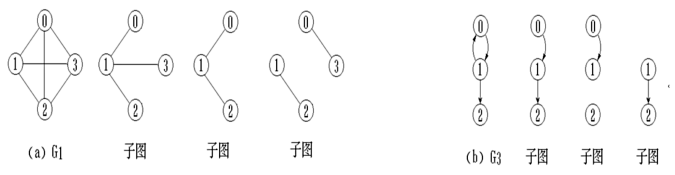
1.无向图中任意两点之间都存在边，称为无向完全图 ; 如G1就是无向完全图。无向完全图具有 n(n-1)/2 条边。
2.有向图中任意两点之间都存在方向向反的两条弧，称为有向完全图; 如G4就是有向完全图。有向完全图具有 n(n-1)条弧。

（4）子图：设两个图G=(V,E)和G’=(V',E’)，如果V'属于V且 E’属于E，则称G’为G的子图

（5）顶点的度、入度和出度

①顶点的度为以该顶点为一个端点的边的数目

②对于无向图，顶点的边数为度，度数之和是顶点边数的两倍

③对于有向图，入度是以顶点为终点(即箭头所指方向)，出度是以顶点为起点(即箭尾巴所指方向)

④有向图的全部顶点入度之和等于出度之和且等于边数。顶点的度等于入度与出度之和。

注意:入度与出度是针对有向图来说的

（6）路径：在图 G=(V,E)中,若从顶点x出发,经过一些顶点v1,...,v2,…,…vm到达顶点y。则称顶点序列(x,v1, v2,…,vm，y)为从顶点x到顶点y的路径。

（7）路径长度：
非带权图的路径长度是指此路径上边的条数。
带权图的路径长度是指路径上各边的权之和。

（8）简单路径：序列中顶点不重复出现的路径。

（9）回路(环)：第一个顶点和最后一个顶点相同的路径。

（10）简单回路(环)：除第一个和最后一个顶点，其余顶点不重复出现的路径

二、图的存储结构

1.邻接矩阵

图的邻接矩阵的存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组(称为邻接矩阵)存储图中的边或弧的信息(可分别称他们为顶点数组和边数组)。

在无向图中，求某个顶点的度，即计算此顶点v在邻接矩阵中第i行(或第i列)的元素之和。若vi到vj之间有通路，则记为1，反之为0。
在有向图中，求某个顶点vi的出度，即求此顶点所在行的元素之和，若求某个顶点的度，即求顶点所在列的元素之和。
设图G有n个顶点，则邻接矩阵是一个n*n的方阵A。

邻接矩阵表示法的优缺点：

优点： （1）便于判断两个顶点之间是否有边，即根据A[i][j]=0或1来判断（2）便于计算各个顶点的度。对于无向图，邻接矩阵第i行元素之和就是顶点i的度;对于有向图，第i行元素之和就是顶点i的出度，第i列元素之和就是顶点i的入度

缺点：
（1）不便于增加和删除顶点
（2）不便于统计边的数目，需要扫描邻接矩阵所有元素才能统计完毕，时间复杂度为 O(n2)
（3）空间复杂度高

2.邻接表

对图中的每个顶点建立一个单链表，存储该顶点所有邻接顶点及其相关信息。每一个单链表设有一个表头结点。把从一个顶点出发的所有边链接在一个单链表(又名边链表)中。把所有边链表的表头结点放在一个顺序表(又名顶点表)中。

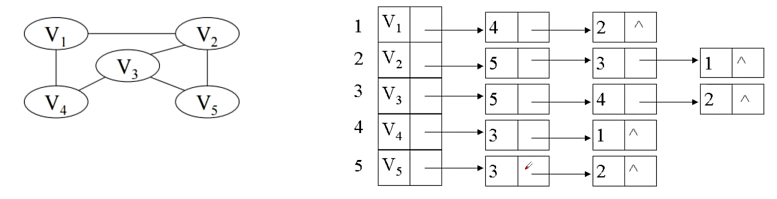
邻接表表示法的优缺点:

优点:
(1)便于增加和删除结点
(2)便于统计边的数目
(3)空间效率高

缺点:
(1)不便于判断顶点之间是否有边2.不便于计算有向图各个顶点的度(需要遍历)

三、图的遍历

从图中某一顶点出发访问图中其余结点，使每一个结点被访问且仅被访问依次

图的遍历通常有两种方法：深度优先搜索和广度优先搜索。它们对无向图和有向图都适用

1.深度优先搜索

深度优先搜索思想:假设初始状态是图中所有顶点均未被访问，则从某个顶点v出发，首先访问该顶点，然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图，直至图中所有和v有路径相通的顶点都被访问到。若此时尚有其他顶点未被访问到，则另选一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。
深度优先搜索是一个递归的过程。首先，选定一个出发点后进行遍历，如果有邻接的未被访问过的节点则继续前进。若不能继续前进，则回退一步再前进，若回退一步仍然不能前进，则连续回退至可以前进的位置为止。重复此过程，直到所有与选定点相通的所有顶点都被遍历。

深度优先遍历类似于二叉树的先序遍历，深度优先遍历通常借助栈来实现算法

深度优先搜索的序列不是唯一的

代码实现：

void dfs(graph g,vtxptr v0){
//从v0出发深度优先遍历图G
//G是连通图或非连通图中的一个连通分量访问v0；w = v0 的第一个邻接点；while(当邻接点w存在时){if(w未访问)dfs(G,w);//若w未访问，则深度优先遍历图w = 下一邻接点；}
}//dfs

2.广度优先搜索

广度优先搜索思想:从图中某顶点v出发，在访问了v之后依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使得先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问，直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问，则需要另选一个未曾被访问过的顶点作为新的起始点，重复上述过程，直至图中所有顶点都被访问到为止。

广度优先搜索类似于树的层次遍历，是按照一种由近及远的方式访问图的顶点。在进行广度优先搜索时需要使用队列存储顶点信息。

广度优先遍历通常借助队列来实现算法

代码实现：

void bfs(graph g,vtxptr v0){
//从v0出发广度优先遍历图g（g是连通图或连通分量）visite(v0);mark[v0] = 1;initqueue(Q);enqueue(Q,v0);//v0进队列Qwhile(!queueempty(Q)){delqueue(Q,v);w = 求v第一个的邻接点；while(当邻接点w存在时){if(w未访问){visite(w);mark[w] = 1;enqueue(Q,w);}w = 下一邻接点；}}
}

四、图的应用：拓扑排序

用顶点、边表示活动和彼此相互关系的网络，简称 AOV网络(Activity On Vertices)

顶点:一个工程中的活动(Actifity)

边:活动的顶点间的优先关系(Relation)

要解决的问题是：将各个顶点（代表各个活动）排列成一个线性有序的序列，使得AOV网络中所有应存在的前驱和后继关系都能得到满足

在AOV网络中，如果活动Vi必须在活动Vj之前进行，则存在有向边<Vi,Vj>，AOV网络中不能出现有向回路，即有向环。在AOV网络中如果出现了有向环，则意味着某项活动应以自己作为先决条件。因此，对给定的AOV网络，必须先判断它是否存在有向环

将各个顶点(代表各个活动)排列成一个线性有序的序列，使得AOV网络中所有应存在的前驱和后继关系都能得到满足——拓扑序列。这种构造AOV网络全部顶点的拓扑有序序列的运算就叫做拓扑排序。即将有向图中的顶点排成一个拓扑序列的过程。

首先建立(n个顶点的)AOV网(1)在AOV网络中选一个没有直接前驱的顶点(入度为0的顶点)，并输出之;(2)从图中删去该顶点，同时删去所有它发出的边重复(1)和(2)，直到全部顶点均已输出，拓扑有序序列形成，拓扑排序完成;若图中还有未输出的顶点，但已跳出处理循环。这说明图中存在环。

算法思想：

(1)建立入度为零的顶点栈;
(2)当入度为零的顶点栈不空时,重复执行 (2)-1 从顶点栈中退出一个顶点,并输出; (2)-2 从AOV网络中删去这个顶点和它发出的边,边的终顶点入度减一;
(2)-3 如果边的终顶点入度减至0,则该顶点进入度为零的顶点栈; (3)如果输出顶点个数少于AOV网络的顶点个数则报告网络中存在有向环。

代码：