【C++】红黑树

1.红黑树的概念

是一种二叉搜索树，在每个节点上增加一个存储位表示节点的颜色，Red或black，通过对任何一条从根到叶子的路径上各个结点着色方式的限制，确保没有一条路径会比其他路径长出俩倍，是接近平衡的。

2.红黑树的性质

1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的，则它的两个孩子结点必须是黑色的 ,任何路径没有连续的红色节点
4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，每条路径上黑色节点数量相等
5. 每个NIL叶子结点都是黑色的

为什么满足上面的性质，红黑树就能保证：其最长路径中节点个数不会超过最短路径节点个数的两倍？

通过该图结合性质3，4就能满足

3.红黑树的实现

3.1节点的定义

enum Colur
{RED,BLACK
};
template<class k,class v>
struct RBTreeNode
{RBTreeNode<k, v>* _left;RBTreeNode<k, v>* _right;RBTreeNode<k, v>* _parent;pair<k, v> _kv;Colur _col;BLTreeNode(const pair<k, v>& kv):_left(nullptr), _right(nullptr), _parent(nullptr),_kv(kv),_col(RED){ }
};

与AVL树相比，将平衡因子替换成颜色。

为什么默认将新插入节点颜色给成红色？
因为给黑色导致该路径黑色节点增加，红黑树性质每条路径上黑色节点数量相同，这样会导致所有路径节点发生变化。而给红色，当前路径违反了不能有两个连续红色节点性质，进行局部颜色调整和旋转即可。

3.2插入操作

1. 按照二叉搜索的树规则插入新节点
2. 检测新节点插入后，红黑树的性质是否造到破坏
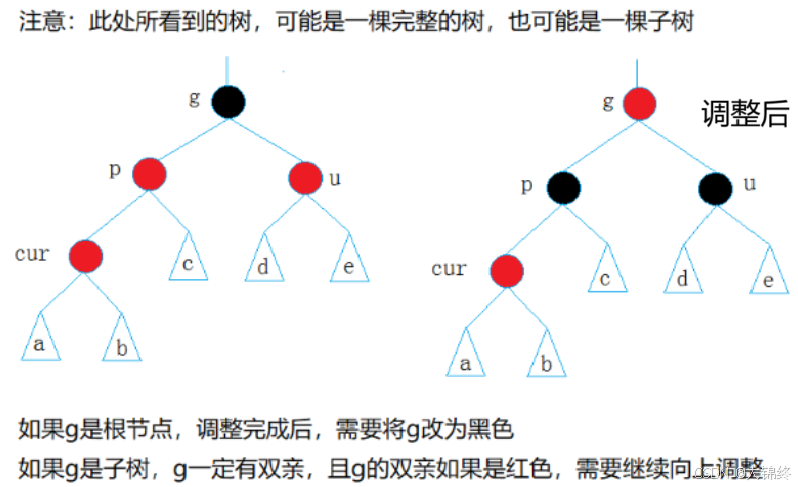
   约定cur为当前节点，p为父节点，g为祖父节点，u为叔叔节点

• 情况一：cur为红，p为红，g为黑，u存在且为红

这是一般规律下的抽象图，下面用一个特例图来帮助我们更好理解情况1的实现过程

• 情况二：cur为红，p为红，g为黑，u不存在/u存在且为黑

总结：
红黑树插入关键看uncle
1.uncle存在且为红，变色+继续往上更新
2.uncle不存在，uncle存在且为黑，旋转+变色

bool Insert(const pair<k, v>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//查找插入位置Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{//找到相同键值return false;}}//插入新节点cur = new Node(kv);cur->_col = RED;if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent&&parent->_col==RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;//uncle存在且为红if (uncle && uncle->_col == RED){//变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//更新节点.继续向上处理cur= grandfather;//注意赋值的顺序parent = grandfather->_parent;}else//uncle不存在或为黑{//判断是单旋还是双旋if (cur == parent->_left){//	  g//	p//cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//    g//  p//	  cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else//parent == grandfather->_right{Node* uncle = grandfather->_left;//uncle存在且为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//更新节点.继续向上处理cur= grandfather;parent = grandfather->_parent;}else//uncle不存在或为黑{//判断是单旋还是双旋if (cur == parent->_right){//g  //  p//    cRotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//g//  p//cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;
}

代码思路：
1.查找插入位置，创建节点并插入，进行平衡调整。
2.平衡调整中循环成立条件为：父节点存在且颜色为红。因为新插入节点为红，父节点也为红，意味着存在两个连续的红色节点，违反红黑树性质，此时需要通过变色和旋转来修复树的性质。
3.在循环中确定祖父节点和叔叔节点。通过判断叔叔节点来进行操作，如上文总结。
4.当父节点不存在或为黑色时调整结束。

3.3验证

1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)

将红黑树按中序遍历的方式存入vector中，通过前后比较元素看是否满足升序

bool IsBST() {vector<int> result;_Inorder(_root,result);for (int i = 1; i < result.size(); i++) {if (result[i] <= result[i - 1]) {return false;}}return true;
}
void _Inorder(Node* root, vector<k>& result) {if (root == nullptr) {return;}_Inorder(root->_left, result);result.push_back(root->_kv.first);_Inorder(root->_right, result);
}

2.检测是否满足红黑树性质

• 检查颜色

bool CheckColur(Node* root, int blacknum, int benchmark)
{//走到null后判断黑色节点数量与基准值是否相同if (root == nullptr){//判断是否违反每条路径中黑色节点数量必须相同if (blacknum != benchmark){return false;}return true;}//判断树中黑节点数量if (root->_col==BLACK){blacknum++;}//判断树中是否有连续红节点情况if (root->_col == RED && root->_parent && root->_parent->_col == RED){cout << root->_kv.first << "出现连续红色节点" << endl;return false;}return CheckColur(root->_left, blacknum, benchmark)&& CheckColur(root->_right, blacknum, benchmark);
}

注意：

这里第二个参数blacknum不传引用刚刚好，这样可以正确的递归计算每一条路径黑色节点数量，返回时由于不是传引用，blacknum作为临时变量随着栈帧的销毁而销毁，不会影响到另一条路径黑色节点数量的计算

//封装接口，提供外界使用
bool IsBalance()
{return IsBalance(_root);
}
bool IsBalance(Node* root)
{if (root == nullptr){return true;}if (root->_col != BLACK){return false;}//计算基准值，随便计算一条路径黑节点的数量int benchmark = 0;Node* cur = root;while (cur){if(cur->_col==BLACK)benchmark++;//选择一条路径来计算黑节点数量cur = cur->_left;}return CheckColur(root, 0, benchmark);
}

3.4红黑树与AVL树的比较

都是高效的平衡二叉树，增删改查的时间复杂度都是O($lo{g}_{2}N$)，红黑树不追求绝对平衡，其只需保证最长路径不超过最短路径的2倍，相对而言，降低了插入和旋转的次数，所以在经常进行增删的结构中性能比AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多。

4.整体代码

• RBTree.h

#pragma once
#include<iostream>
#include<vector>
using namespace std;enum Colur
{RED,BLACK
};
template<class k,class v>
struct RBTreeNode
{RBTreeNode<k, v>* _left;RBTreeNode<k, v>* _right;RBTreeNode<k, v>* _parent;pair<k, v> _kv;Colur _col;RBTreeNode(const pair<k, v>& kv):_left(nullptr), _right(nullptr), _parent(nullptr),_kv(kv),_col(RED){ }
};template<class k,class v>
struct RBTree
{typedef RBTreeNode<k, v> Node;
public:bool Insert(const pair<k, v>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//查找插入位置Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{//找到相同键值return false;}}//插入新节点cur = new Node(kv);cur->_col = RED;if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent&&parent->_col==RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;//uncle存在且为红if (uncle && uncle->_col == RED){//变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//更新节点.继续向上处理cur= grandfather;//注意赋值的顺序parent = grandfather->_parent;}else//uncle不存在或为黑{//判断是单旋还是双旋if (cur == parent->_left){//	  g//	p//cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//    g//  p//	  cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else//parent == grandfather->_right{Node* uncle = grandfather->_left;//uncle存在且为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//更新节点.继续向上处理cur= grandfather;parent = grandfather->_parent;}else//uncle不存在或为黑{//判断是单旋还是双旋if (cur == parent->_right){//g  //  p//    cRotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//g//  p//cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}void RotateL(Node* parent){_rotateCount++;Node* cur = parent->_right;Node* curleft = cur->_left;Node* ppnode = parent->_parent;//第一次改变链接parent->_right = curleft;if (curleft){curleft->_parent = parent;}//第二次改变链接cur->_left = parent;parent->_parent = cur;//判断根节点的链接情况//为根节点调整平衡因子情况if (parent == _root){_root = cur;cur->_parent = nullptr;}//树中的部分调整情况else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}void RotateR(Node* parent){_rotateCount++;Node* cur = parent->_left;Node* curright = cur->_right;Node* ppnode = parent->_parent;//第一次链接parent->_left = curright;if (curright){curright->_parent = parent;}//第二次链接cur->_right = parent;parent->_parent = cur;//调整根节点链接关系if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}bool CheckColur(Node* root, int blacknum, int benchmark){if (root == nullptr){if (blacknum != benchmark){return false;}return true;}//判断树中黑节点数量if (root->_col==BLACK){blacknum++;}//判断树中是否有连续红节点情况if (root->_col == RED && root->_parent && root->_parent->_col == RED){cout << root->_kv.first << "出现连续红色节点" << endl;return false;}return CheckColur(root->_left, blacknum, benchmark)&& CheckColur(root->_right, blacknum, benchmark);}bool IsBalance(){return IsBalance(_root);}bool IsBalance(Node* root){if (root == nullptr){return true;}if (root->_col != BLACK){return false;}//计算基准值int benchmark = 0;Node* cur = root;while (cur){if(cur->_col==BLACK)benchmark++;//选择一条路径来计算黑节点数量cur = cur->_left;}return CheckColur(root, 0, benchmark);}int Height(){return Height(_root);}int Height(Node* root){if (root == nullptr){return 0;}int leftheight = Height(root->_left);int rightheight = Height(root->_right);return leftheight > rightheight ?leftheight + 1 : rightheight + 1;}bool IsBST() {vector<int> result;_Inorder(_root,result);for (int i = 1; i < result.size(); i++) {if (result[i] <= result[i - 1]) {return false;}}return true;}void _Inorder(Node* root, vector<k>& result) {if (root == nullptr) {return;}_Inorder(root->_left, result);result.push_back(root->_kv.first);_Inorder(root->_right, result);}public:int _rotateCount = 0;private:Node* _root = nullptr;
};

• 测试代码

#include"AVLTree.h"
#include"RBTree.h"
#include<vector>//int main()
//{
//	//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
//	int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
//	RBTree<int, int> t;
//	for (auto e : a)
//	{
//		t.Insert(make_pair(e, e));
//		cout << "Insert:" << e << "->" << t.IsBalance() << endl;
//	}
//
//	return 0;
//}int main()
{const int N = 1000000;vector<int>v;srand(time(0));v.reserve(N);for (size_t i = 0; i < N; i++){v.push_back(i);}AVLTree<int, int>avlt;for (auto e : v){avlt.Insert(make_pair(e, e));}cout << avlt.IsBalance() << endl;cout << avlt.Height() << endl;cout << avlt._rotateCount << endl;cout << avlt.IsBST() << endl;RBTree<int, int>rbt;for (auto e : v){rbt.Insert(make_pair(e, e));}cout << rbt.IsBalance() << endl;cout << rbt.Height() << endl;cout << rbt._rotateCount << endl;cout << rbt.IsBST() << endl;return 0;
}