当前位置：首页 > news >正文

【C】初阶数据结构15 -- 计数排序与稳定性分析

news 来源：原创 2025/8/4 18:23:56

本文主要讲解七大排序算法之外的另一种排序算法 -- 计数排序

1 计数排序

1）算法思想

2）代码

3）时间复杂度与空间复杂度分析

（1）时间复杂度

（2）空间复杂度

4）计数排序的优点与缺点

（1）优点

（2）缺点

2 排序的稳定性

1）稳定性的定义

2）七大排序算法的稳定性分析

3）七大排序算法时空复杂度与稳定性总结

3 总结

1 计数排序

计数排序是排序算法中最简单的一种算法，不需要借助递归等算法，不过需要一点哈希表的思想（哈希表是一种数据结构，后面 C++ 部分会有相应的讲解，本质就是通过一个函数将元素值转化为其对应的映射，从而快速找到其值的一个数据结构）。

1）算法思想

计数排序的算法思想如同其名字一样，就是计算出其每个元素出现的次数，然后进行排序，其算法过程如下：

a. 先找出其数组中的最大值 maxnum 与最小值 minnum，然后动态开辟一个 maxnum - minnum + 1 空间大小的数组 count

b. 然后用一个变量 i 遍历原数组，假设原数组为 arr，然后每次让 count[arr[i] - minnum]++

c. 再用一个变量 i 遍历 count 数组，再创建一个 index 下标，初始为 0，如果 count[i] != 0，那就让arr[index] = i + minnum，然后 index++，count[i]--，直到 count[i] 变为 0 为止。

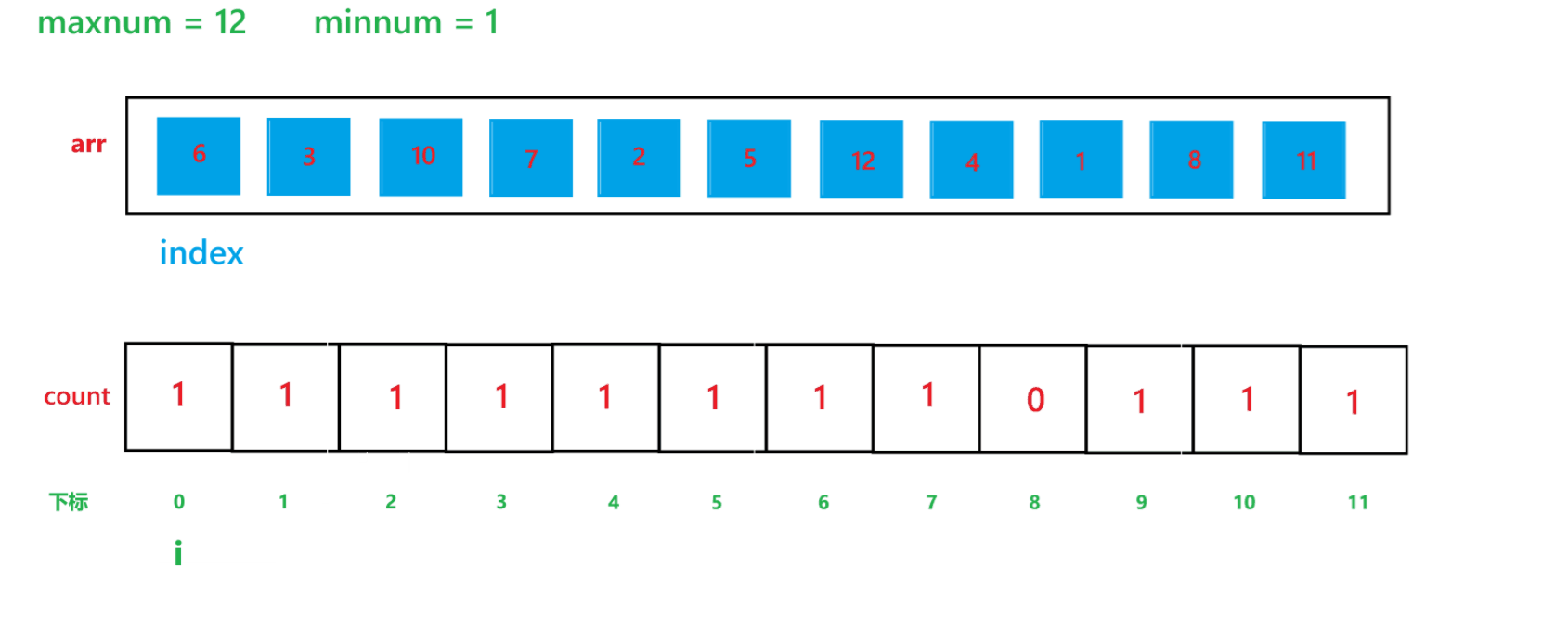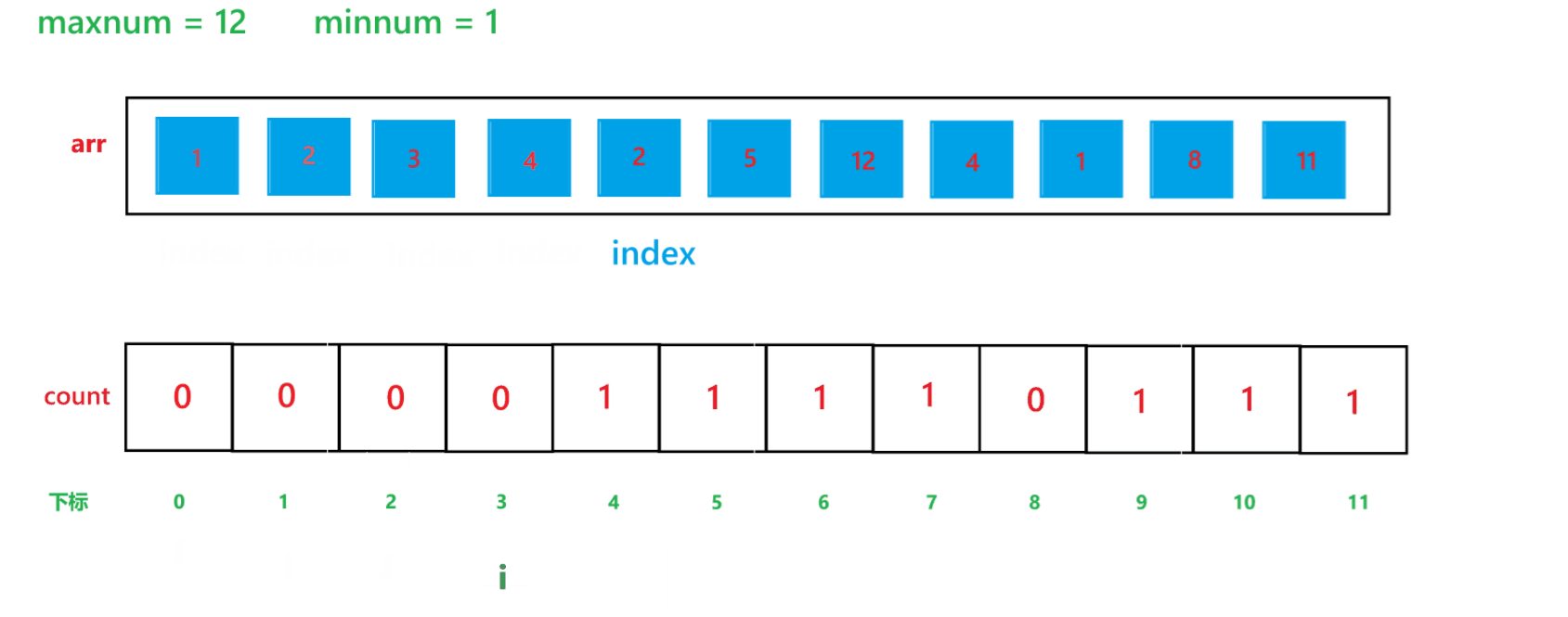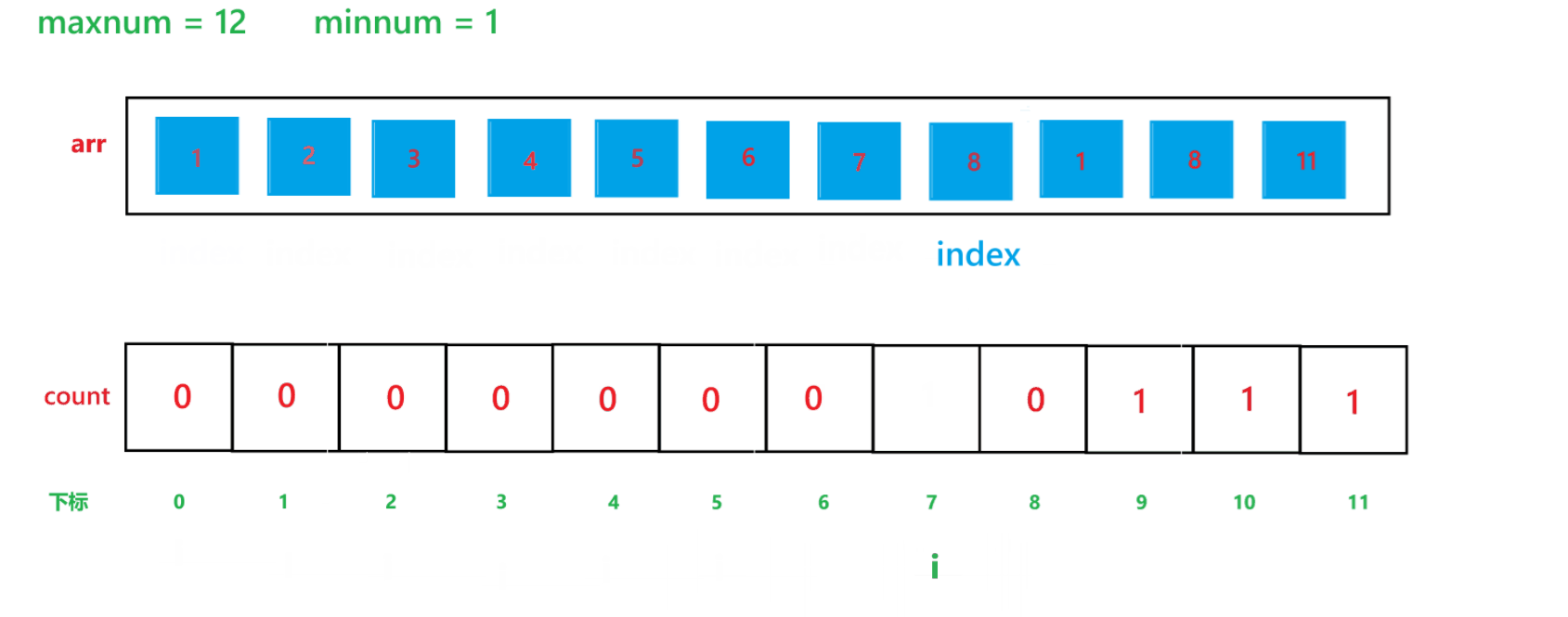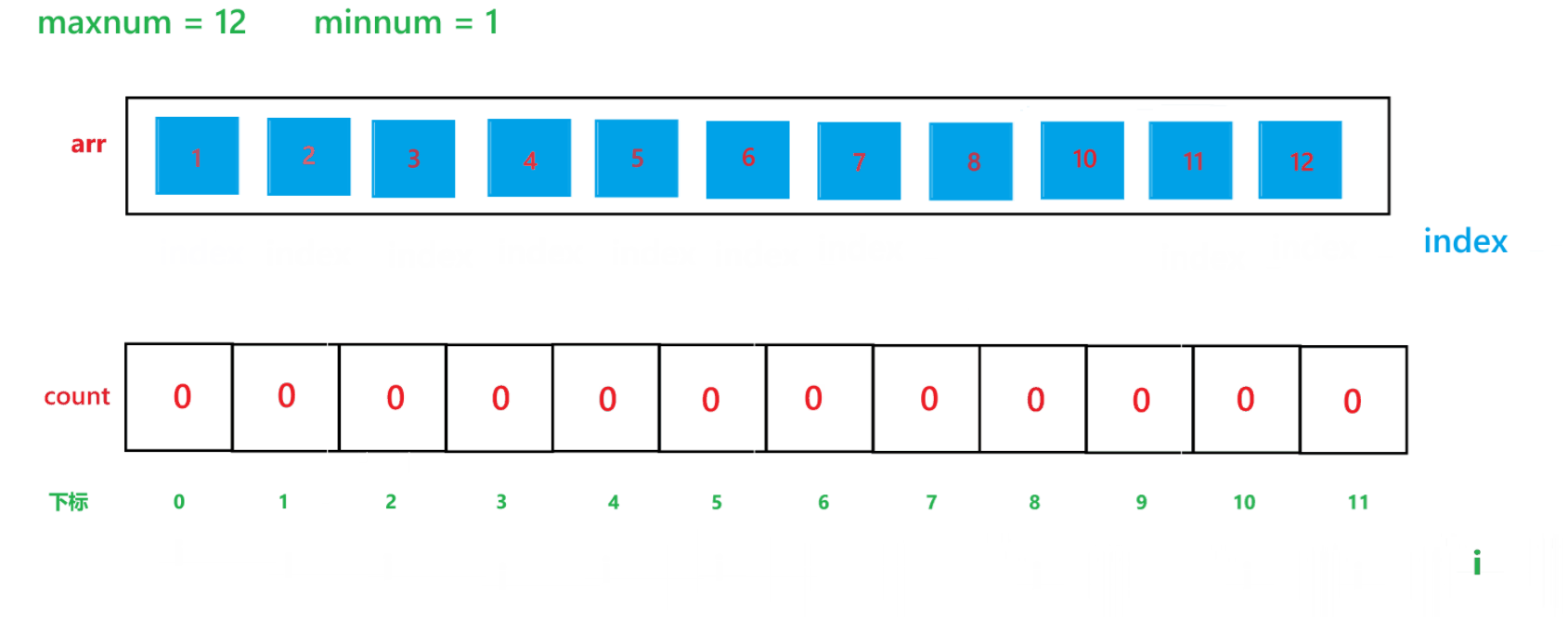
其算法思想本质就是通过 arr 数组中每个元素减去最小值计算出 arr 数组中每个元素在 count 数组中的下标映射，然后越小的元素就在 count 数组中处于越前面的位置，count[i] 就记录了每个元素出现的次数。其执行过程如下：
（1） count 数组变化的过程：

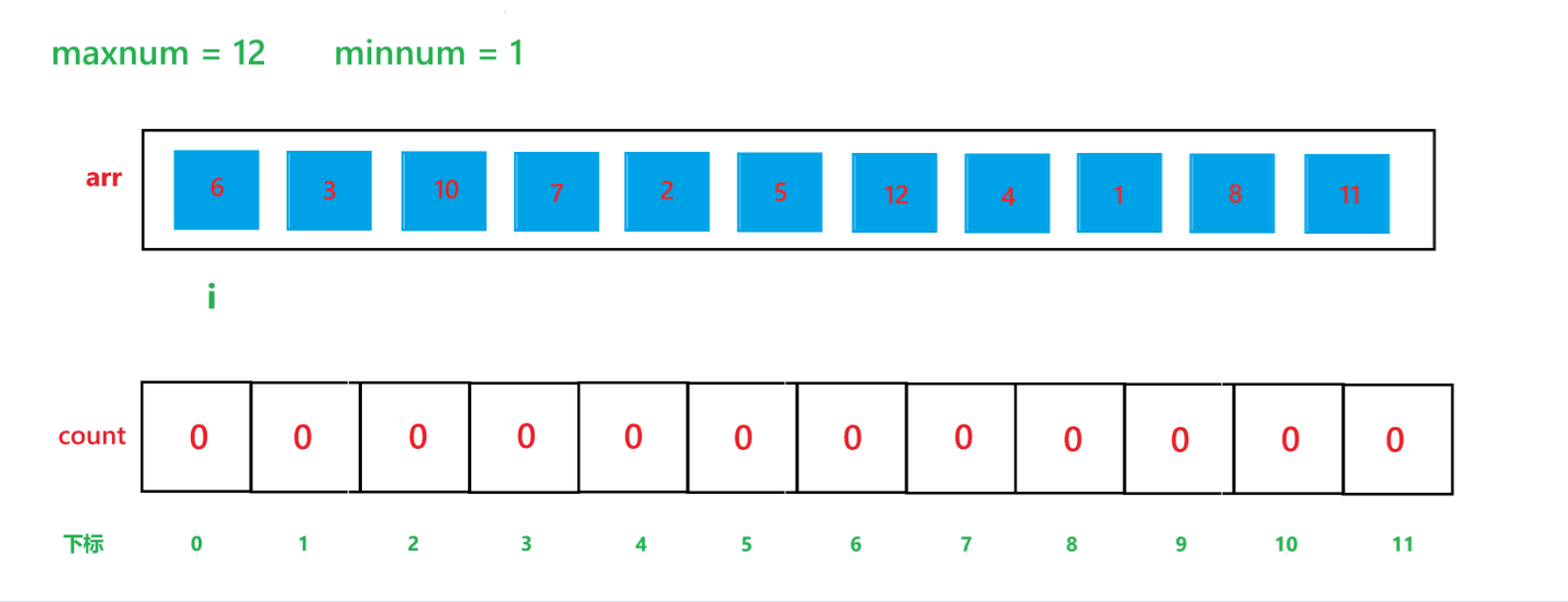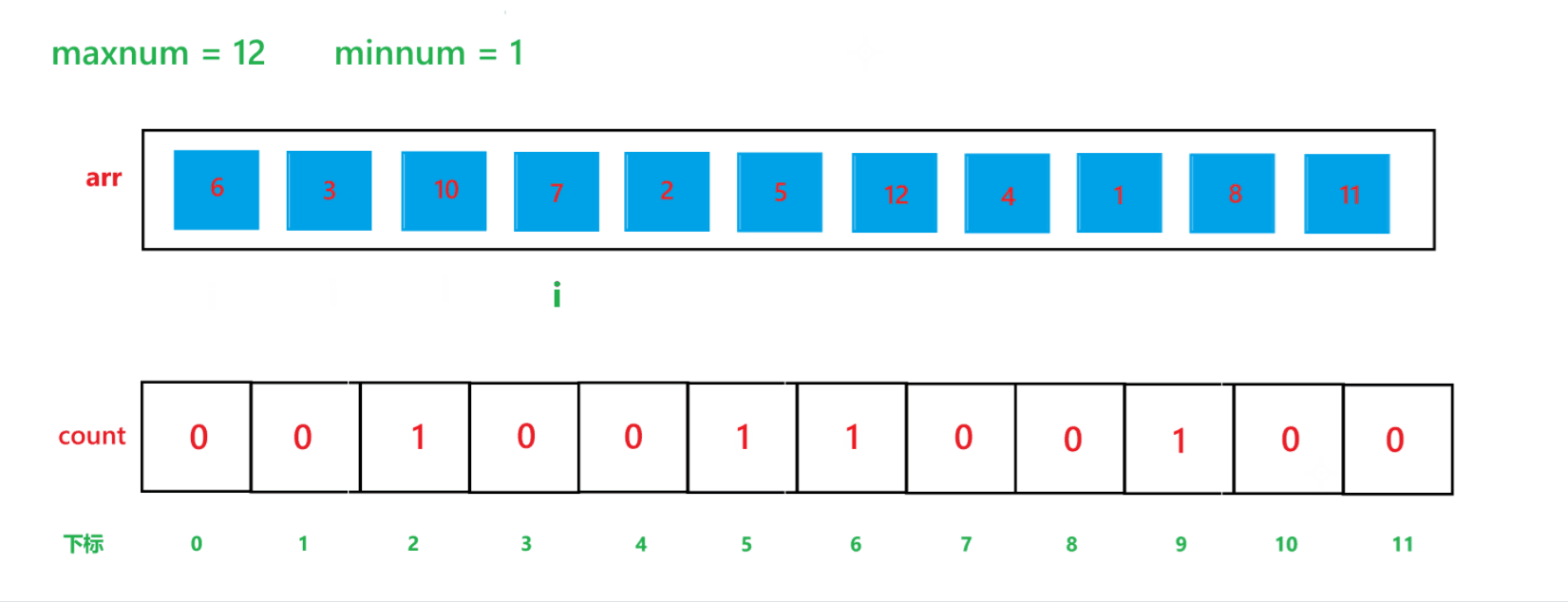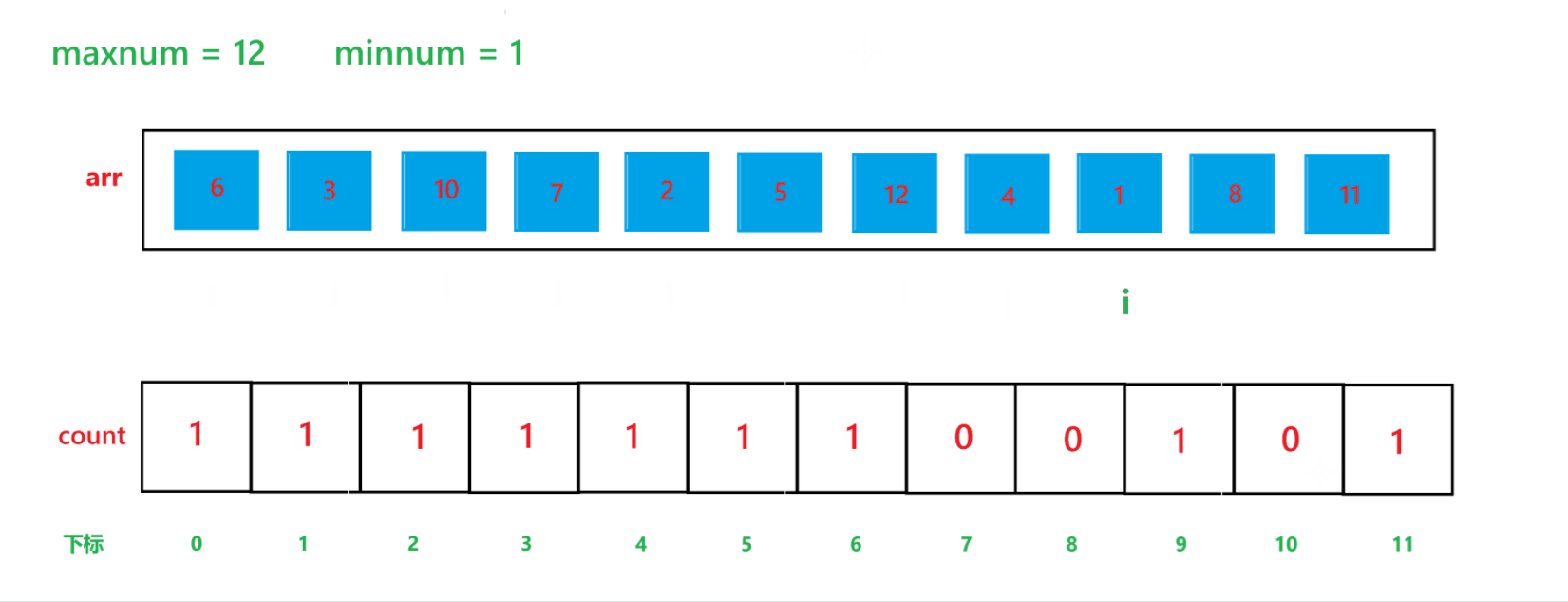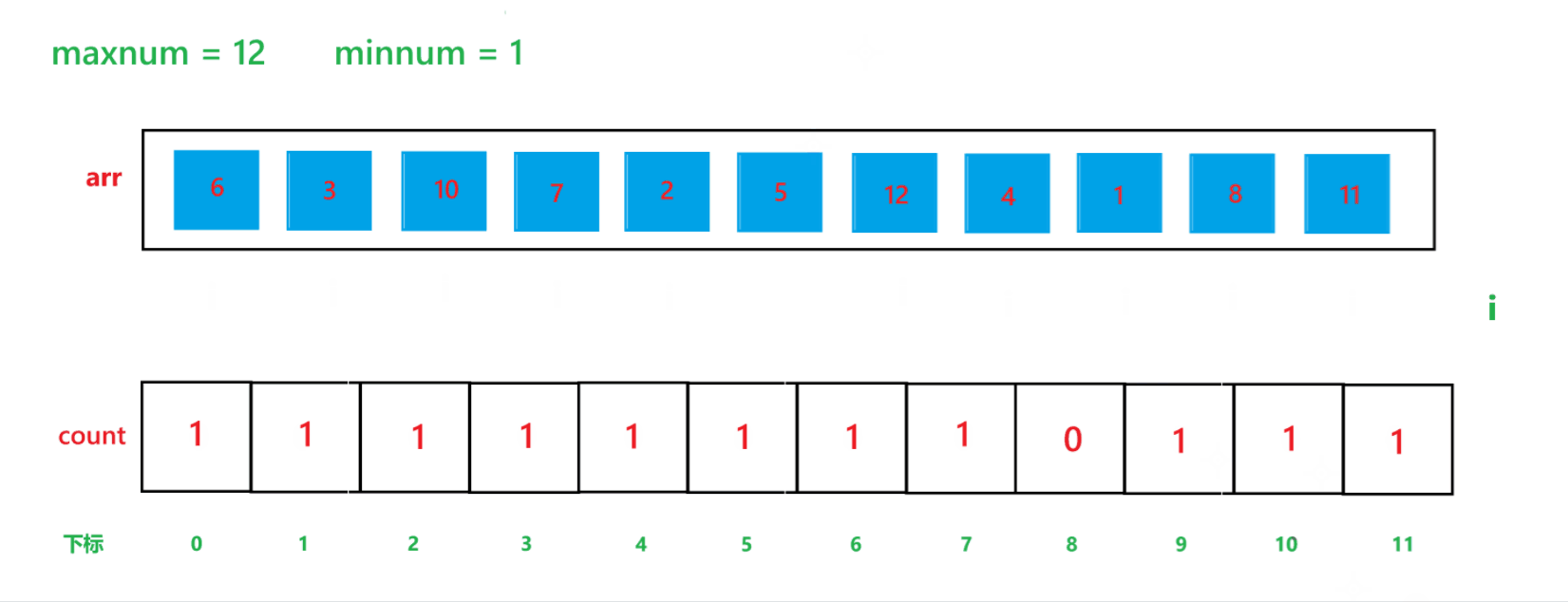
（2） arr 数组变化过程：

2）代码

void CountSort(int* arr, int n)
{//先找最大值和最小值int maxnum = 0, minnum = INT_MAX;for (int i = 0; i < n; i++){if (maxnum < arr[i]) maxnum = arr[i];if (minnum > arr[i]) minnum = arr[i];}//开辟数组空间int* count = (int*)calloc(maxnum - minnum + 1, sizeof(int));if (count == NULL){perror("malloc fail！\n");exit(1);}//遍历原数组，count记录出现次数for (int i = 0; i < n; i++){count[arr[i] - minnum]++;}//再遍历count数组，将元素放到 arr 数组中int index = 0;for (int i = 0; i < maxnum - minnum + 1; i++){while (count[i]){arr[index++] = i + minnum;count[i]--;}}
}

这里有个需要注意的一点，就是动态开辟 count 数组空间的时候，要使用 calloc 函数，因为 count 数组里面的值必须全都初始化为 0，如果用 malloc 函数的话里面是随机值，是会发生错误的。

测试用例：

#include<stdio.h>
#include<stdlib.h>int main()
{int arr[] = { 6, 3, 10, 7, 2, 5, 12, 4, 1, 8, 11 };int n = sizeof(arr) / sizeof(arr[0]);CountSort(arr, n);for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");return 0;
}

3）时间复杂度与空间复杂度分析

（1）时间复杂度

从代码来分析，尽管有里面有两层循环，但是里面的 count[i] 循环仅有常数次，假设这里的 maxnum - minnum + 1 = k，计数排序的时间复杂度为 T(n) = O(n + k)。

（2）空间复杂度

假设 maxnum - minnum + 1 为 k，由于动态开辟了 k 个空间，所以空间复杂度为 S(n) = O(k)。

4）计数排序的优点与缺点

（1）优点

计数排序的优点特别明显，就是其时间复杂度比较低，执行效率很高；前面的七大排序算法最快的时间复杂度就是 O(nlogn)，所以计数排序的执行效率是比前面任何一个排序的执行效率都快。

（2）缺点

但是计数排序也有明显的缺点，由于在排序过程中需要动态开辟 maxnum - minnum + 1 的空间，所以如果 maxnum 与 minnum 相差很大时，需要动态开辟的空间就很大，会浪费很多空间；所以如果 arr 数组中的数据相差很大，比较离散时，计数排序的消耗就会很大。

综合来说，计数排序的应用场景比较有限，如果 arr 数组中的数据很集中时，应用计数排序就很合适，效率很高；但如果数据比较离散的话，计数排序就不太适合了，消耗会比较大。

2 排序的稳定性

1）稳定性的定义

一个排序算法是否稳定是指：如果对于一组数据，其中有相等的值，如果进行排序之后，之前相等的值的相对位置保持不变，那就称该排序算法是稳定的，否则就是不稳定的。比如：有一组数据 1 8 5 8 7，假设第一个 8 为 num1，第二个数据为 num2，排序之前 num1 排在 num2 之前，排完序之后，该组数据变为 1 5 7 num1 num2，num1 还是排在 num2 之前，就称该排序算法是稳定的；假如排完序之后，num1 排在了 num2 之后，那么该排序算法就是不稳定的。

2）七大排序算法的稳定性分析

冒泡排序：假设一组数据为 8 8 2 1，第一个 8 为 num1，第二个 8 为 num2（num1 num2 2 1），那么根据冒泡排序的算法思想，第一轮排序的结果应该为 num1 2 1 num2，第二轮为 2 1 num1 num2，第三轮排序结果为 1 2 num1 num2。经过排序之后，发现 num1 还是排在 num2 之前，所以冒泡排序算法是稳定的。

直接插入排序：还是假设数据为 num1 num2 2 1（同冒泡排序），经过第一轮排序，结果仍为 num1 num2 2 1，第二轮排序结果为 2 num1 num2 1，第三轮排序结果为 1 2 num1 num2。排完序之后，num1 依然排在 num2 之前，所以直接插入排序也是稳定的。

归并排序：依然假设数据为 num1 num2 2 1，num1 与 num2 合并之后依然是 num1 num2，2 与 1 合并之后结果为 1 2，然后两个子数组再进行合并，结果为 1 2 num1 num2。排完序之后，num1 依然排在 num2 之前，所以归并排序也是稳定的。

直接选择排序：假设一组数据为 num1 8 num2 2 9 （5 8 5 2 9），第一轮排序之后结果为 2 8 num2 num1 9，发现 num1 跑到 num2 之后了，所以直接选择排序是不稳定的。究其原因，就是因为直接选择排序会将最大的与每轮排序中的最后一个位置交换，将最小的和每轮排序中的第一个位置交换，就有能会使相同元素的相对位置发生变化。

希尔排序：假设一组数据为 num1 8 2 num2 9 （5 8 2 5 9），第一轮排序 num1 2 9 一组，8 num2 一组，排完序之后结果就变为了 2 num2 num1 8 9，此时 num2 与 num1 相对位置发生了变化，所以希尔排序也是一种不稳定的排序算法。

堆排序：假设一组数据为 num1 num2 num3 num4 （2 2 2 2），第一次排序会将 num1 与 num4交换（堆顶元素与最后一个元素交换），此时结果变为了 num4 num2 num3 num1，相对位置发生了变化，所以堆排序也是一种不稳定的排序算法。

快速排序：假设一组数据为 5 num1 num2 4 num3 8 9 10 11（5 3 3 4 3 8 9 10 11），第一次排序，key值为 5，cur 在后面找比 5 小的元素然后和 ++prev 位置交换（双指针算法找 key 值），所以第一次排序之后结果为 num3 num1 num2 4 5 8 9 10 11，此时相对位置发生了变化，所以快速排序算法也是一种不稳定的排序算法。

3）七大排序算法时空复杂度与稳定性总结

以下表格是对七大排序的时空复杂度以及稳定性的总结：

七大排序算法总结
排序算法	时间复杂度	空间复杂度	稳定性
直接插入排序	O(n^2)	O(1)	稳定
直接选择排序	O(n^2)	O(1)	不稳定
希尔排序	O(n^1.3)	O(1)	不稳定
冒泡排序	O(n^2)	O(1)	稳定
堆排序	O(nlogn)	O(1)	不稳定
快速排序	O(nlogn)	O(logn) ~ O(n)	不稳定
归并排序	O(nlogn)	O(n)	稳定

3 总结

到这里，初阶数据结构的知识就已经结束了，我们来回顾一下：在初阶数据结构里面，我们学习了顺序表、链表、栈、队列以及二叉树这五种数据结构，学习了 8 种排序算法；不仅通过具体代码实现了每个数据结构，而且还通过具体题目来加深了对于数据结构的理解，相信在学习完初阶数据结构之后，代码能力肯定会提升很多。

在之后，我们会开启新的模块的学习，包括 C++语言、Linux操作系统以及高阶数据结构和各种经典算法，比如递归、回溯、动态规划、双指针算法等，在后面的文章中会交叉更新不同内容，后面的难度也肯定会呈不断递增的趋势，但是只要继续学下去，肯定就会收获满满，所以不要放弃哦！

1 计数排序

1） 算法思想

2） 代码

3） 时间复杂度与空间复杂度分析

（1） 时间复杂度

（2） 空间复杂度

4） 计数排序的优点与缺点

（1） 优点

（2） 缺点

2 排序的稳定性

1） 稳定性的定义

2） 七大排序算法的稳定性分析

3） 七大排序算法时空复杂度与稳定性总结

3 总结

相关文章：

1）算法思想

2）代码

3）时间复杂度与空间复杂度分析

（1）时间复杂度

（2）空间复杂度

4）计数排序的优点与缺点

（1）优点

（2）缺点

1）稳定性的定义

2）七大排序算法的稳定性分析

3）七大排序算法时空复杂度与稳定性总结