当前位置：首页 > news >正文

动态规划--两个数组的dp问题

news 来源：原创 2025/8/7 8:32:06

1 最长公共子序列

2 最长回文子序列

3 不相交的线

4 不同的子序列

5 通配符匹配

6 正则表达式匹配

7 交错字符串

8 两个字符串的最小ASCII删除和

9 最长重复子数组

本文主要讲解两个数组的动态规划问题的几个经典例题，希望看完本文之后能够对大家做这一类问题时有所帮助。

1 最长公共子序列

1143. 最长公共子序列 - 力扣（LeetCode）

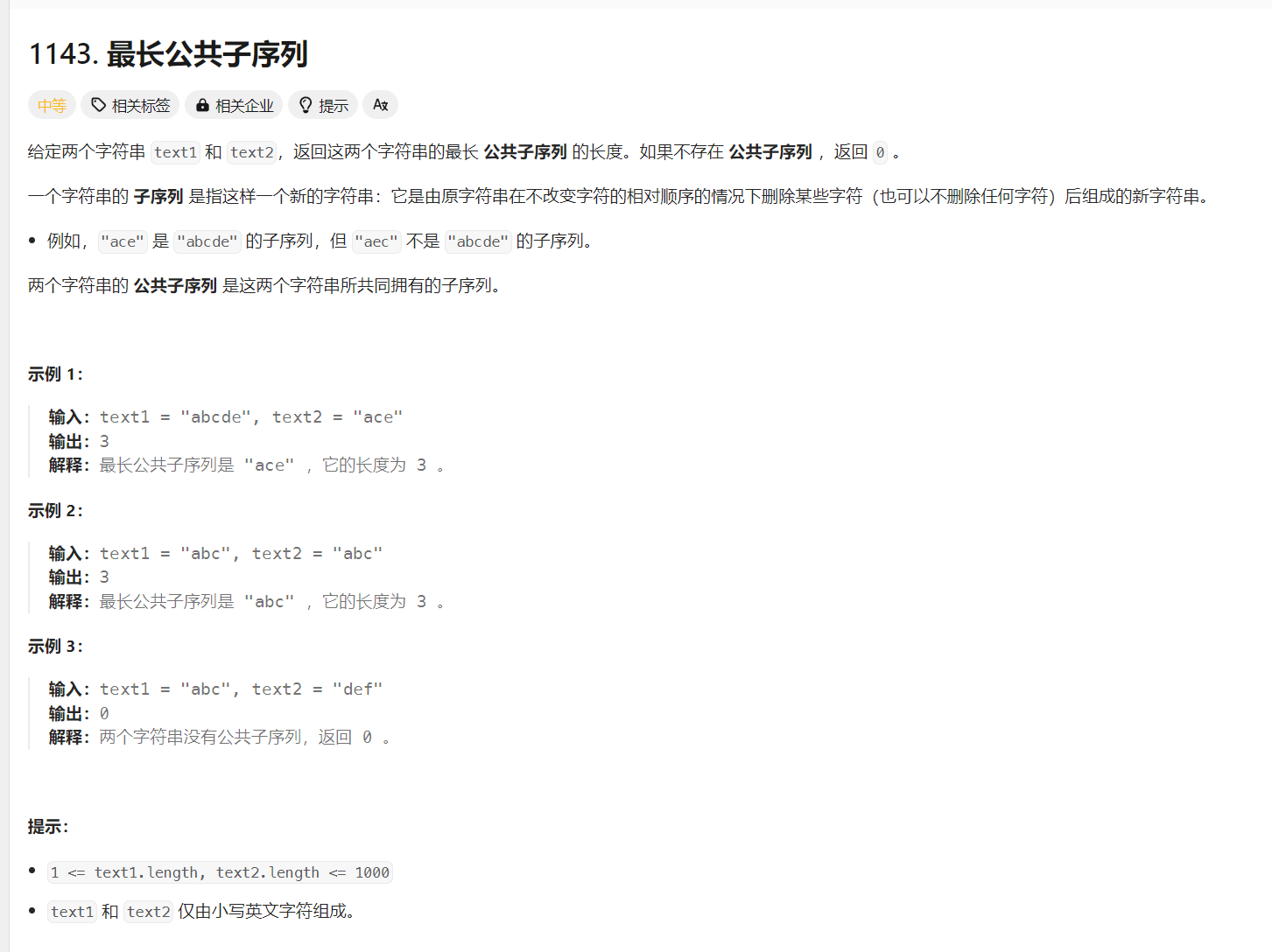
题目解析：题目给定两个字符串，要求我们求出两个字符串的最长公共子序列的长度，公共子序列顾名思义就是完全相同的子序列。

对于这种两个字符串或者两个数组的子序列的问题，我们用基础的以某个数组的某个位置为结尾，..... ，这样的状态表示，其实已经无法满足题目要求了，因为我们需要在两个数组上做动态规划，至少需要保存两个数组的各自的状态，那么我们一般的状态表示模板就是

dp[i][j] 表示数组1以i位置为结尾，数组2以j位置为结尾，......

或者 dp[i][j] 表示数组1的[0.i]区间，数组2的[0,j]区间，......

那么对于本题，我们的状态表示就是：

dp[i][j] 表示text1中[0,i]范围内的所有子序列和text2中[0,j]范围内的所有子序列中，最长公共子序列的长度。

状态转移方程推导：

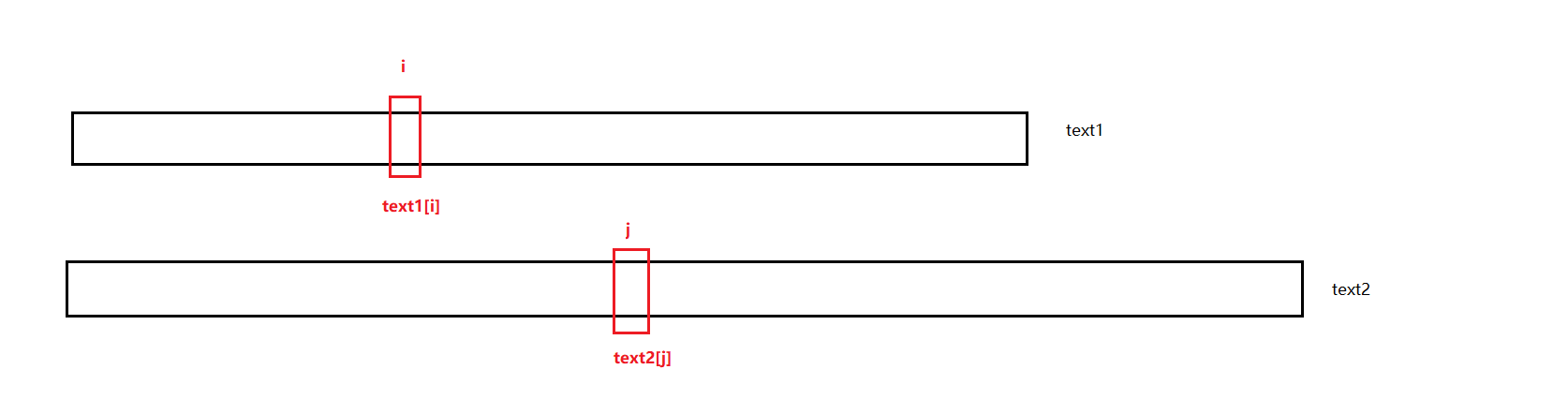
对于text1和text2中以i位置和j位置为结尾的子序列中，我们要求的是最长公共子序列的长度，那么对于结尾位置，我们需要考虑两种情况：

1、 text1[i] == text2[j] ，那么对于这两个区间内的最长公共子序列，我们选择 text1[i] 和 text2[j] 作为公共子序列的结尾字符是最优的，那么两个区间的剩余部分就是： text1中以i-1为结尾的子序列，以及text2中以j-1为结尾的子序列，我们需要找出剩余区间的最长公共子序列，然后各自加上text1[i] 和 text2[j] 这两个字符，组成新的最长的公共子序列，那么此时dp[i][j] = 1 + dp[i-1][j-1]

2、text1[i] != text2[j] ，那么说明dp[i][j]的最长公共子序列必然不可能同时包含text1[i]和text2[j]，最多包含其中一个，有可能最长公共子序列是以 text1[i]为结尾的，有可能是以text2[j]为结尾的，也有一种可能就是这两个都不是最长公共子序列的结尾，那么此时我们就需要看两个区间的除去这两个位置的剩余区间的最长公共子序列，也就是dp[i-1][j-1]。

那么对于第2种情况，三种情况分别是 dp[i][j-1]，dp[i-1][j]，以及dp[i-1][j-1]，但是由于 dp[i-1][j-1] 所计算的区间其实是 dp[i][j-1] 和 dp[i-1][j]的子区间，所以 dp[i-1][j-1] <= min(dp[i][j-1],dp[i-1][j])，那么我们在填表计算的时候，因为需要的是最大的长度，所以我们不需要考虑吧dp[i-1][j-1]。

那么综上而言，状态转移方程如下：

if(text1[i] == text2[j]) dp[i][j] = 1 + dp[i-1][j-1];
else dp[i][j] = max(dp[i-1][j] , dp[i][j-1]);

细节问题：

初始化：由于填写dp[i][j]的时候，会用到dp[i-1][j] 和 dp[i][j-1]以及dp[i-1][j-1] ，那么当我们填写 i=0和j=0的时候会越界，那么我们需要手动初始化这些位置或者说开额外的空间来避免越界。

那么如果开额外空间，也就是多开一行和一列，此时dp[0][j]表示的就是text1的[0,-1] 的所有子序列和text2 的[0,j-1]的所有子序列的最长公共子序列的长度，而由于[0,-1]是非法区间，我们可以认为他的子序列只有空子序列，那么其实他们没有公共子序列，长度就是0。同理，dp[i][0]也是0。那么我们可以多开一行和一列，然后把所有的值初始化为0.

填表顺序：从上往下填写每一行，每一行中从左往右填写每一列。

返回值：我们需要的是两个字符串的最长公共子序列，那么返回值就是 dp[m][n] ，m为text1的长度，n为text2的长度。

代码如下：

class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int m = text1.size() , n = text2.size();vector<vector<int>> dp(m+1,vector<int>(n+1));for(int i = 1 ; i <= m ; ++i){for(int j = 1 ; j <= n ; ++j){if(text1[i-1] == text2[j-1]) dp[i][j] = 1 + dp[i-1][j-1];else dp[i][j] = max(dp[i-1][j] , dp[i][j-1]);}}return dp[m][n];}
};

2 最长回文子序列

516. 最长回文子序列 - 力扣（LeetCode）

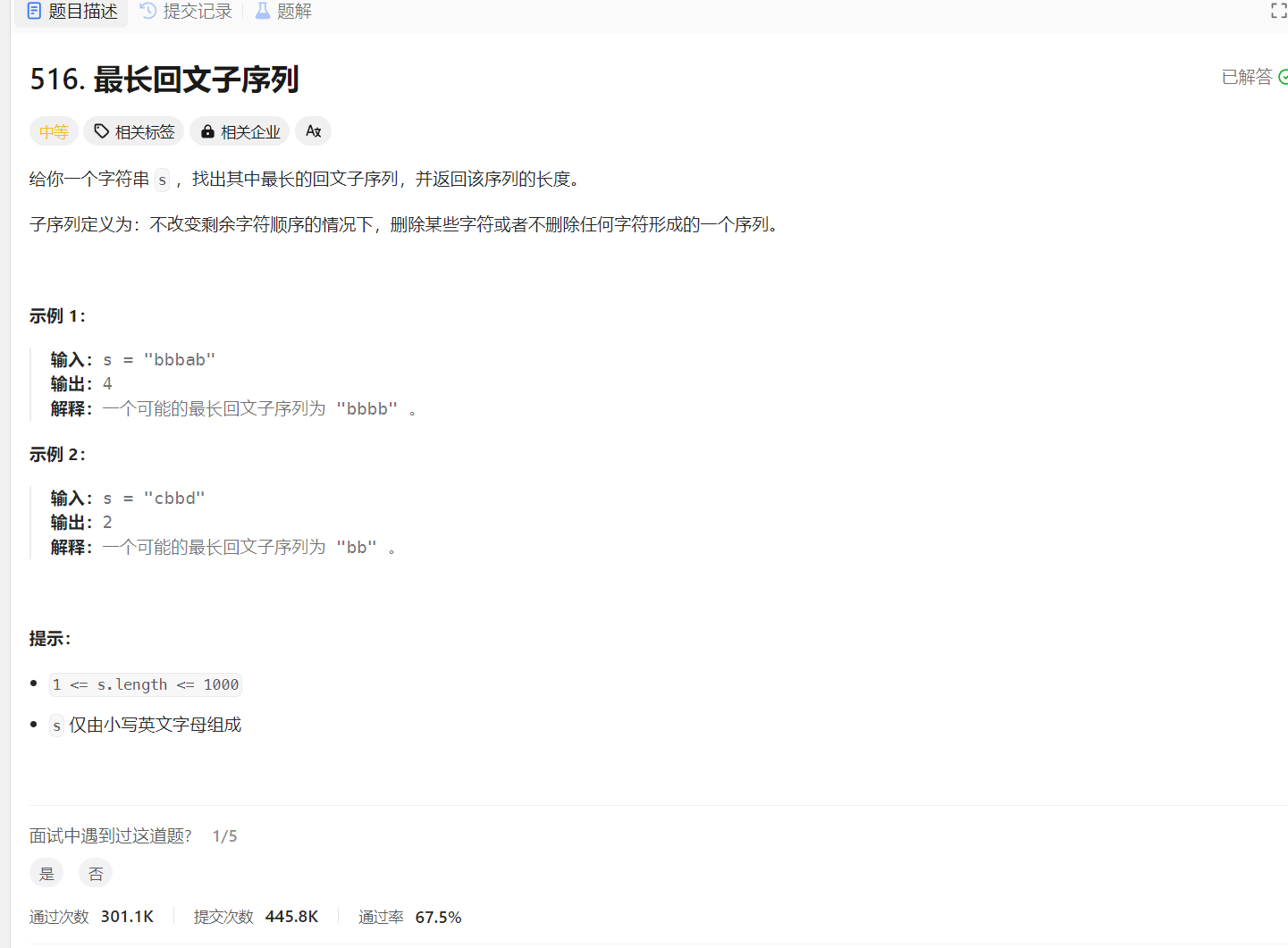
本题我们在回文子序列文章中将结果，当时是使用子序列的做法来完成的，而我们对于这个题也可以使用公共子序列的做法来做。

首先需要一个 s 的逆置字符串，定义为s1，那么s1和s的最长公共子序列就是s的最长大的回文子序列。

为什么呢？因为回文子序列正着读和反着读是一样的，也就是说整个子序列是关于中心位置对称的，那么对于这个最长的回文子序列，如果我们将整个字符串逆置过来，那么回文子序列也相当于进行了逆置操作，但是他和逆置之前是一模一样的。那么我们只需要找到某个序列，他在原字符串s中和在s1中是一样的，那么他就是回文子序列。

至于动态规划的思路就和第一题一样，我们就不再过多讲解。

代码如下：

class Solution {
public:int longestPalindromeSubseq(string s) {int n = s.size();string s1(s.rbegin() , s.rend());vector<vector<int>> dp(n+1,vector<int>(n+1));for(int i = 1 ; i <= n ; ++i){for(int j = 1 ; j <= n ; ++j){if(s[i-1] == s1[j-1]) dp[i][j] = dp[i-1][j-1] + 1;else dp[i][j] = max(dp[i-1][j] , dp[i][j-1]);}}return dp[n][n];}
};

这种做法的时间复杂度还是O(n^2)，但是空间复杂度从O(n)变成了O(n^2)，但是对于本题还是可以解决的。

3 不相交的线

1035. 不相交的线 - 力扣（LeetCode）

解析题目：本题从题目意思上来看是一个连线问题，好像和动态规划没有多大关系，但是我们可以将题目意思进行转换。我们要找到两个数组中相同的值，然后可以进行连线，但是所有的连线不能相交。

也就是说如果在 nums1和nums2中存在 i1 和 j1 这条连线，那么不能再出现 i > i1 && j < j1的连线，否则就是相交的。

本题我们可以看测试用例1，只有相等的点才能连线，那么我们就能够想到公共子序列了，选取两个数组的公共子序列，对应的位置进行连线。

那么公共子序列为什么不会出现相交的线呢?因为刚刚子序列中每个元素的相对位置和其在原数组中的相对位置是一致的。公共子序列是原数组删除一些位置的元素之后剩余的元素，那么我们可以反过来，在两个公共子序列都加上一些元素，由于这些新加的元素是不进行连线的，所以他们不会影响公共子序列的连线，那么在公共子序列中连线不相交，在原数组中这些连线也不会香蕉。

那么本题的做法和前面两个题完全一致，就是一个公共子序列的题。

代码如下：

class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {int m = nums1.size() , n = nums2.size();vector<vector<int>> dp(m+1,vector<int>(n+1));for(int i = 1 ; i <= m ;++i){for(int j = 1 ; j <= n ; ++j){if(nums1[i-1] == nums2[j-1]) dp[i][j] = 1 + dp[i-1][j-1];else dp[i][j] = max(dp[i-1][j] , dp[i][j-1]);}}return dp[m][n];}
};

4 不同的子序列

115. 不同的子序列 - 力扣（LeetCode）

解析题目：我们需要求出在s的所有子序列中，t 出现的个数。这个题我们需要对 t 进行拆分来思考。首先，要使得 s 的某一个子序列为 t ，那么首先该子序列的最后一个字符就需要是t的最后一个字符。同时，那么假设 s[i] = t.back()，也就是说，s的i位置元素就是t的最后一个字符，那么s中以i为结尾的所有自子序列中有多少个 t 呢？而以 i 位置为结尾的子序列可以看成是 i 之前的子序列后面加上一个 s[i]，那么在 i 位置之前，有多少个子序列是 t(0,len-1) 的子串，在他们后面加上一个 s[i]，就变成了 t。

比如 s[i] = ‘c' ,t = "abbc",那么s[i] == t.back(),那么以s[i]为结尾的所有的子序列中，和 t相同的子序列的个数就是s的[0,i-1]区间内有多少个 "abb" 的子序列，在他们的后面加上一个s[i] 就构成了与t相等的子序列。

而 s 的 [0,i-1]的所有子序列中有多少了 t 的[0,j]的子串，就有转换为了子问题。

那么我们的状态表示可以定义为：
dp[i][j] 表示在 s 的[0,i]范围内有多少个子序列和 t 的[0,j]子串相同。

状态转移方程推导：

对于dp[i][j]，如果s[i] == t[j]，那么在s的[0,i]范围内的子序列中，等于t的[0,j]子串的数量就取决于在s的[0,i-1]区间中的所有子序列中有多少个 t 的[0,j-1]子串，那么此时 dp[i][j] = dp[i-1][j-1]。但是这一部分子序列只是在s的[0,i]范围内以 s[i] 为结尾的子序列中和 t[0,j]相等的数量，还有一部分子序列不以s[i]为结尾，但是也和 t的[0,j]区间相等，那么此时还需要将这一部分计算进去。那么不以s[i]为结尾的和t的[0,j]子串相等的子序列的个数就是 dp[i-1][j]，也就是在s的[0,i-1]范围内所有的和t的[0,j]子串相等的子序列的个数。那么dp[i][j] = dp[i-1][j-1] + dpi-1][j];

如果s[i] != t[j] ，那么说明在s的[0,i]范围内，和t的[0,j]子串相等的子序列，都不会以s[i]为结尾或者说都不会包含s[i]，那么此时在[0,i]范围内的和t的[0,j]字串相等的子序列的个数其实就取决于在s的[0,i-1]范围内有多少个t的[0,j]子串。也就是 dp[i][j] = dp[i-1][j];

对于[0,i]范围内的所有子序列中，需要划分为两种情况：1、包含i位置的子序列 2、不包含i位置的子序列

那么综上所述，状态转移方程为：

$dp[i][j] = dp[i-1][j] + (s[i] == t[j] ?dp[i-1][j-1] : 0)$

细节问题：

初始化：由于填 dp[i][j]的时候会用到dp[i-1][j] 和dp[i-1][j-1]，那么在填 i = 0 或者 j = 0 的时候可能会越界，所有我们需要手动初始化 i=0和j=0的位置，但是我们也可以多开一行和一列的空间来方便我们的初始化。

多开一行和一列，那么对于d[0][j]就表示s的[0,-1]范围内有多少个t[0,j-1]的子序列，由于s的[0,-1]只有空子序列，那么其实不会有和t[0,j]相等的子序列，所以dp[0][j] = 0; 而对于dp[i][0]表示的是s的[0,i-1]范围内有多少个t[0,-1]子串，也就是有多少个空串，那么我们可以理解为有一个空串，也就是空子序列，那么dp[i][0] = 1。同时dp[0][0] = 1。

填表顺序：从上往下填写每一行，每一行中从左往右填写每一列。

返回值：dp[m][n]，m为s的长度，n为t的长度。

整数溢出的问题：要注意，虽然题目说明了最终的返回值不会超出int的范围，但是只是说明dp[i][n]不会溢出，并不代表着 dp[i][x] x<n 不会溢出，所以我们需要使用更大的数据范围。在这个题中，我们使用long long 都有可能超出范围，所以我们需要使用更大的 unsigned long long 来存储。

class Solution {
public:int numDistinct(string s, string t) {int m = s.size() , n = t.size();vector<vector<unsigned long long>> dp(m+1,vector<unsigned long long>(n+1));for(int i = 0 ; i <= m ; ++i) dp[i][0] = 1;for(int i = 1 ; i <= m ; ++i){for(int j = 1 ; j <= n ; ++j){dp[i][j] = dp[i-1][j] + (s[i-1] == t[j-1] ? dp[i-1][j-1] : 0);}}return dp[m][n];}
};

5 通配符匹配

44. 通配符匹配 - 力扣（LeetCode）

解析题目：本题其实就是类似于正则表达式的匹配，特殊字符只有两个，?和 * ， . 可以匹配任何单个字符，但是不能匹配空字符。而 * 可以匹配任意个字符序列，也可以匹配空字符。而其他的字符都是普通字符，只能匹配和他一样的字符。而我们需要判断 p 能否完全匹配 s 。

如果 p 是"*" ，那么这个 * 可以直接匹配 s 的全部字符，不管s是空字符串还是普通字符串。

而如果 p 是"a*"，那么说明只有s的第一个字符为 'a' 时，p才能匹配s。

而如果 p 是 "a?" ，那么说明，s必须包含两个字符同时第一个字符必须为'a'。

如果p是 "a?*"，那么说明s至少需要有两个字符，同时第一个字符必须是'a'。

我们可以发现 '*' ，是最特殊的，它可以匹配空序列。

同时，对于 p="a*" ,如果去匹配 s= "abcd"，可以让p的*首先匹配掉一个 'd' ，但是由于*可以匹配任意多个字符，所以我们p中的 * 还可以继续使用，所以剩下的问题就是 p = "a*"去匹配s = "abc"，以此类推，最后变成了 p = "a*" ，去匹配s = "a"，此时因为 * 的前一个字符和接下来要匹配的字符是可以匹配的，所以我们有两种方式来匹配s中的 'a' ，可以用 * 取匹配空字符，然后 'a'去匹配'a'，也可以 '*' 去匹配 'a' ，然后就变成了 p = "a*"去匹配s=""，这两种方式只要有一种能够成功匹配，那么最终就是能够成功匹配的。

对于这种两个数组的问题，我们定义状态表示为：

dp[i][j] 表示使用 p 的[0,i] 去匹配 s 的[0,j] 能否完全匹配。

那么分析状态转移方程：

首先保证 i <= j ，所以我们只会用到整个dp表的一般空间。

对于 dp[i][j]，使用 p 的[0,i] 去匹配 s 的[0,j] ，我们需要根据 p[i] 划分为三种情况：

1、p[i] = '.' ，那么p[i]必须要匹配 s[0,j]的最后一个字符，那么我们只需要判断剩余部分能否完全匹配就行了，此时 dp[i][j] = dp[i-1][j-1]。

2、p[i] 为普通字符，此时p[i] 必须要匹配 s[j] ，同时p[i]必须要和s[j]相等，如果p[i] == s[j]，那么需要判断剩余部分能否匹配，此时 dp[i][j] = dp[i-1][j-1] ,如果p[i]!=s[j]，那么无法完全匹配，此时dp[i][j] = false;

3、p[i]为'*'，那么p[i]可以匹配任意多个字符，此时p[i]有三种使用方式：

3.1: p[i] 匹配空字符，此时dp[i][j] = dp[i-1][j];

3.2:p[i]匹配一个字符，那么能否完全匹配取决于剩余的部分，此时dp[i][j]=dp[i-1][j-1];

3.3:p[i]匹配多个字符(>1)，那么此时我们可以将'*'传递给前面，此时dp[i][j] = dp[i][j-1]。

而只需要其中一种使用方式能够完全匹配，那么我们就认为可以完全匹配。

综上，我们的状态转移方程为：

if(p[i] == '?') dp[i][j] = dp[i-1][j-1] ;

else if(p[i] == '*') dp[i][j] = dp[i][j-1] || dp[i-1][j-1] || dp[i-1][j] ;

else dp[i][j] = p[i] == s[j] && dp[i-1][j-1]

细节问题：

初始化：由于填写dp[i][j]需要用到 i-1和j-1的位置，所以我们需要手动初始化 i = 0 和 j = 0 的位置。或者我们可以多开一行和多开一列，简化我们的初始化过程。

如果多开一行和一列的话，dp[0][j]表示能否使用 p[0,-1]去匹配s[0,j-1]，此时当然无法匹配，因为相当于用一个空串去匹配一个非空串，那么dp[0][j] = false; dp[i][0]表示使用 p 的[0,i-1]去匹配 s 的[0,-1]也就是用一个非空串去匹配空串，由于 '*'是可以匹配空串的，所以如果 p的[0,i]区间全部都是'*'，那么dp[i][0] 是可以匹配的，直到某一次p[i]!='*'，那么此时和后续的dp[i][0]都为false同时，dp[0][0]使用空串匹配空串是可以的。

那么我们的初始化可以这样做：

        int m = p.size() , n = s.size();vector<vector<bool>> dp(m+1,vector<bool>(n+1,false));dp[0][0] = true;for(int i = 0 ; i < m ; ++i){if(p[i] == '*') dp[i+1][0] = true;else break;}

填表顺序：从上往下填写每一行，每一行中从左往右填写每一列

返回值:dp[m][n] ，m为p的长度，n为s的长度。

代码如下：

class Solution {
public:bool isMatch(string s, string p) {int m = p.size() , n = s.size();vector<vector<bool>> dp(m+1,vector<bool>(n+1,false));dp[0][0] = true;for(int i = 0 ; i < m ; ++i){if(p[i] == '*') dp[i+1][0] = true;else break;}for(int i = 1 ; i <= m ; ++i){for(int j = 1 ; j <= n ; ++j){if(p[i-1] == '?') dp[i][j] = dp[i-1][j-1];else if(p[i-1] == '*') dp[i][j] = dp[i-1][j] || dp[i][j-1] || dp[i-1][j-1];else dp[i][j] = p[i-1] == s[j-1] && dp[i-1][j-1];}}return dp[m][n];}
};

6 正则表达式匹配

10. 正则表达式匹配 - 力扣（LeetCode）

解析题目：本题其实是上一个题目的进阶版本，'.' 还是和上一题的'?'一样，必须匹配单个字符。而'*'则不再是单独使用，而必须要和 '*' 的前一个字符配合使用，如果 '*' 的前面是一个普通字符 x，那么 'x*' 其实就只能用来匹配任意多个 x 字符。如果 '*'前面是 '.' ，".*"是可以匹配任意多个任意字符。而如果'*'的前面是'*'，那么此时这两个'*'其实是可以看成一个'*'的，而"**"能够匹配的字符取决于前面的距离最近的非 '*' 字符。

那么为了简化"**"这种情况，我们可以对 p 进行预处理，首先将所有的连续的'*'变成一个'*'，方便后续分析。题目明确指出了 * 的前面一定是有非 * 字符的，所以我么可以直接预处理。

        //预处理p，将连续出现的'*'变成一个'*'string p1;p1.reserve(p.size());for(int i = 0 ; i < p .size() ; ++i){if(p[i] == '*') //将后面的*都删除，但是由于删除操作erase效率太低，我们不妨直接使用一个新的字符串来存储出路之后的p{int j = i + 1;while(j < p.size()) if(p[j] != '*') break ; else ++j; //遇到*就一直往后遍历//走到这里 j 是i后面的第一个非*字符，或者是越界(最后一个字符也是*)//那么我们将非*字符的前一个*放入p1中i = j - 1;}p1.push_back(p[i]);}

那么接下来的分析其实就和上一个题完全一样了。

定义状态表示为：

dp[i][j] 表示p1[0,i]能否完全匹配s[0,j]

状态转移方程推导：

根据p1[i] 划分为三种情况：

1、p1[i]为普通字符，那么此时p1[i]需要匹配s[j]，同时剩余部分也需要完全匹配，此时dp[i][j] = p1[i] == s[j] && dp[i-1][j-1]

2、p1[i]为 '.'，此时p1[i]需要匹配s[j]，且剩余部分也需要能够完全匹配，此时dp[i][j] = dp[i-1][j-1]

3、p1[i]为'*'，那么此时p1[i] 无法单独使用，必须配合前面的p1[i-1]来使用。那么此时有四种情况：

3.1: p1[i-1] != s[j] ，那么此时 p1[i-1] 和 '*' 只能匹配0个字符，那么dp[i][j] = dp[i-2][j]

3.2: p1[i-1] == s[j]，此时有两种情况，匹配一个字符，此时dp[i][j] = dp[i-1][j] 或者dp[i-2][j-1]

3.3: p1[i-1] == s[j]，匹配多个字符(>1)，也就是将 p1[i-1] 和 * 传递给下一层，此时dp[i][j] =dp[i][j-1].

但是这里有一种更特殊的情况就是p1[i-1]=='.'的时候，那么他是可以匹配任意多个任意字符的。

那么综上，状态转移方程如下：
if(p1[i] == '?') dp[i][j] = dp[i-1][j-1];

else if(p1[i] == '*') dp[i][j] = dp[i-2][j] || ((p1[i-1] == '.' || p1[i-1]==s[j]) &&(dp[i][j-1] || dp[i-2][j-1]);

else dp[i][j] = p1[i] == s[j] && dp[i-1][j-1]

细节问题：

初始化：由于填写dp[i][j]的时候会用到i-1和j-1,(i-2其实用到的是 -1，因为当p1[i]=='*'的时候i>=1)，那么我们需要初始化i=0和j=0的位置或者使用虚拟空间，多开一行和多开一列。

如果多来一行和多开一列，此时dp[0][j]表示使用p1[0,-1]来匹配s的[0,j-1]，当j > 0 的时候dp[0][j] = false;同时dp[0][0] = true; 而dp[i][0]表示使用p1[0,i-1]来匹配s[0,-1]，也就是使用非空串去匹配空串，由于在这里 "x*" 可以匹配 0 个字符，所以p1[0,i]都是 "x*"的组合的话，还是可以匹配空串的，此时 p1 的所有的奇数下标元素都是 *，但是对于其偶数位置,dp[i][0]还是为false。我么可以这样初始化：

        int m = p1.size() , n = s.size();vector<vector<bool>>dp(m+1,vector<bool>(n+1,false));dp[0][0] = true;//然后判断p1的奇数位置是否为 * ,注意 p1[i]对应dp表中的 dp[i+1]for(int i = 1 ; i < p1.size() ; i += 2){if(p1[i] == '*') dp[i+1][0] = true;else break;}

同时多开一行和一列之和要注意映射关系发生了变化。

填表顺序：从上往下填写每一行，每一行中从左往右填写每一列。

返回值：dp[m][n]，m为p1的长度，n为s的长度。

代码如下：

class Solution {
public:bool isMatch(string s, string p) {//预处理p，将连续出现的'*'变成一个'*'string p1;p1.reserve(p.size());for(int i = 0 ; i < p .size() ; ++i){if(p[i] == '*') //将后面的*都删除，但是由于删除操作erase效率太低，我们不妨直接使用一个新的字符串来存储出路之后的p{int j = i + 1;while(j < p.size()) {if(p[j] != '*') break ;else ++j; //遇到*就一直往后遍历}//走到这里 j 是i后面的第一个非*字符，或者是越界(最后一个字符也是*)//那么我们将非*字符的前一个*放入p1中i = j - 1;}p1.push_back(p[i]);}   cout<<"p1:"<<p1<<endl;int m = p1.size() , n = s.size();vector<vector<bool>>dp(m+1,vector<bool>(n+1,false));dp[0][0] = true;//然后判断p1的奇数位置是否为 * ,注意 p1[i]对应dp表中的 dp[i+1]for(int i = 1 ; i < p1.size() ; i += 2){if(p1[i] == '*') dp[i+1][0] = true;else break;}for(int i = 1 ; i <= m ; ++i){for(int j = 1 ; j <= n ; ++j){if(p1[i-1] == '.')dp[i][j] = dp[i-1][j-1];else if(p1[i-1] == '*') dp[i][j] = dp[i-2][j] ||((p1[i-2] == '.' || p1[i-2] == s[j-1]) && (dp[i-2][j-1] || dp[i][j-1]));else dp[i][j] = p1[i-1] == s[j-1] && dp[i-1][j-1];}}return dp[m][n];}
};

7 交错字符串

97. 交错字符串 - 力扣（LeetCode）

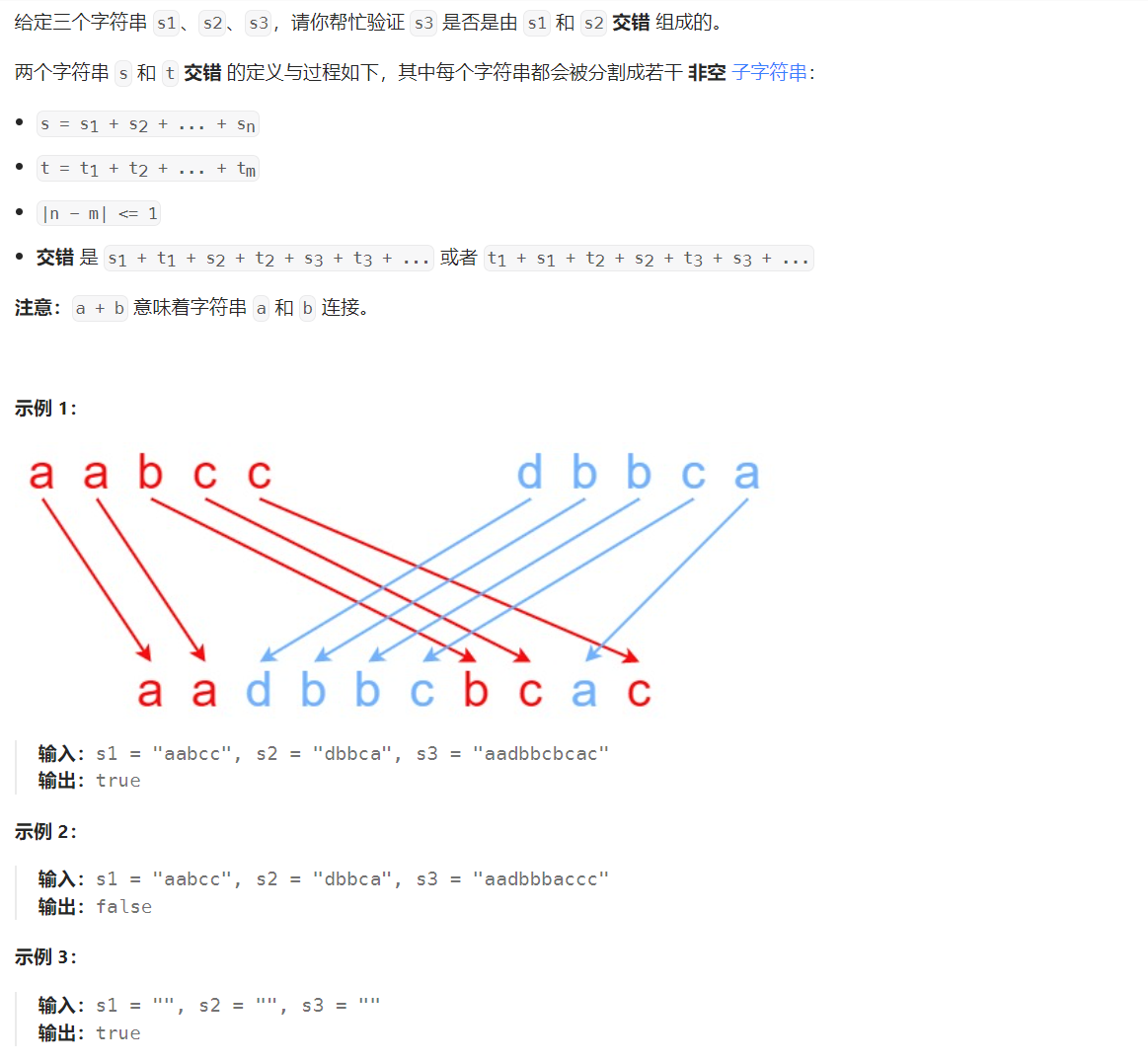
解析题目：本题要求验证 s3 能否由 s1和s2交错而成，这里的交错不好理解，我们可以换一种理解：不改变 s1 和 s2 中字符的相对顺序，能否构成s3。

那么第一眼看可能我们会认为这里是三个字符串的dp问题，可能需要一个三维dp表来划分出三个字符串的区间，但是仔细想一下，我们如果确定了 s1 和 s2 的区间，也就是确定了这两个区间的长度，那么s3的某个区间要由这两个区间构成，那么首先长度一定时能够确定的，那么我们只需要用一个二维dp表就行了。

定义状态标识如下：

dp[i][j] 表示能否由s1的[0,i] 和 s2的[0,j] 构成s3的[0,i+j+1]

状态转移方程推导：

对于dp[i][j]，是使用s1的[0,i]区间和s2的[0,j]区间来交替构成s3的[0,i+j+1]区间，那么我们可以根据s3的区间的最后一个字符分成三种情况：

1、s1[i] == s3[i+j+1]，此时可以由s1的区间的最后一个字符作为s3的区间的最后一个字符，那么就需要看s3剩余的部分能否被s1和s2的剩余区间构成，此时 dp[i][j] = dp[i-1][j]。

2、s2[j] == s3[i+j+1]，此时可以由s2的区间的最后一个字符作为s3的区间的最后一个字符，那么也需要看剩余部分能够由s1和s2的剩余部分构成，此时dp[i][j] = dp[i][j-1]。

3、s1[i] != s3[i+1+j] && s2[j] != s3[i+j+1] ，此时s1的[0,i]区间和s2的[0,j]区间一定无法交替构成s3的[0,i+j+1]区间，那么此时dp[i][j] = false;

当然还有可能就是s1[i]=s2[j]=s3[i+j+1]，此时只要任何一种情况能够为true，那么最终结果就是true。

那么我们的状态转移方程如下:

dp[i][j] = false;

if(s1[i] == s3[i+j+1]) dp[i][j] = dp[i][j] || dp[i-1][j];

if(s2[j] == s3[i+j+1]) dp[i][j] = dp[i][j] || dp[i][j-1];

细节问题：

初始化:由于填写dp[i][j]可能用到 i-1 和 j-1，那么我们需要手动初始化i=0和j=0的位置，也可以多开一行和一列来便于初始化。

多开一行和一列时，dp[0][j]表示能否由s1[0,-1]和s2[0,j] 构成s3[0,j]，那么此时只需要能否由s2构成s3的牵绊部分就行了。 dp[i][0]也是一样的，看能否由s1构成s3的前半部分。而dp[0][0]表示能否由s1和s2的空串构成s3的空串，当然可以，所以dp[0][0] = true;

填表顺序：从上往下填写每一行，每一行从左往右填写每一列。

返回值：dp[m][n] ，m为s1的长度，n为s2 的长度。

代码如下：

class Solution {
public:bool isInterleave(string s1, string s2, string s3) {if(s1.size() + s2.size() != s3.size()) return false;int m = s1.size() , n = s2.size();vector<vector<bool>> dp(m+1,vector<bool>(n+1,false));dp[0][0] = true;//初始化dp[0][j]，看能否由s2构成s3的前半部分[0,n)for(int j = 0 ; j < n; ++j){if(s3[j] == s2[j]) dp[0][j+1] = true;else break;}//看能否由s1构成s3的前半部分[0,m)for(int i = 0 ; i < m ; ++i){if(s1[i] == s3[i]) dp[i+1][0] = true;else break;}for(int i = 1 ; i <= m ; ++i){for(int j = 1 ; j <= n ; ++j){//dp[i][j]映射：s1[0,i-1]和s2[0,j-1]能否构成s3[0,i+j-1]if(s1[i-1] == s3[i+j-1]) dp[i][j] = dp[i][j] || dp[i-1][j];if(s2[j-1] == s3[i+j-1]) dp[i][j] = dp[i][j] || dp[i][j-1];}}return dp[m][n];}
};

8 两个字符串的最小ASCII删除和

712. 两个字符串的最小ASCII删除和 - 力扣（LeetCode）

解析题目：本题其实相对于前面的题要简单很多，给定两个字符串，为了让两个字符串相等，我们需要删除两个字符串中的某些字符，返回删除的字符的ASCII码值的总和。

直接定义状态标识如下：

dp[i][j]表示使s1的[0,i]和s2的[0,j]相等的最小ASCII删除和。

状态转移方程推导：

对于dp[i][j]，要使s1[0,i]和s2[0,j]相等，首先需要保证这两个子区间的最后一个字符相等。

1、最后一个字符相等s1[i] == s2[j]，那么最后一个字符可以保留到最后，用于构成相等的字符串，那么我们还需要保证剩余区间[0,i-1]和[0,j-1]相等，所以最小删除和为：dp[i][j] = dp[i-1][j-1];

2、最后一个字符不相等，那么s1[i]和s2[j]不可能同时保留到最后，他们两个至少需要删除一个，当然也有可能最终这两个字符都要删除，如果删除s1[i]，那么dp[i][j] = dp[i-1][j] + s1[i]；如果删除s1[j]，那么dp[i][j] = s2[j] + dp[i][j-1]。那么最终dp[i][j]填的就是这两种情况的较小值。当然还可能两个都需要删除，但是我们无法在填写dp[i][j]的时候判定是否需要两个删除，这是一个包含在dp[i][j-1]和dp[i-1][j]中的问题，我们在填写这两项的时候就已经考虑过了。

本题由于数据量很小，只有2000，那么可以直接使用int来存储。

综上，状态转移方程为：

if(s1[i] == s2[j]) dp[i][j] = dp[i-1][j-1];

else dp[i][j] = min(s1[i] + dp[i-1][j] , s2[j] + dp[i][j-1]

细节问题：

初始化：我们需要手动初始化i=0和j=0的位置，也可以多开一行和一列空间。

如果多开一行和一列的话，dp[0][j]表示的是使s1的[0,-1]和s2的[0,j-1]相等的最小删除ASCII和，那么此时我们只需要遍历累加s2的和就行了。dp[i][0]也是类似。同时dp[0][0] = 0;

填表顺序：从上往下填写每一行，每一行从左往右填写每一列。

返回值：dp[m][n] ，m为s1的长度，n为s2的长度。

代码如下：

class Solution {
public:int minimumDeleteSum(string s1, string s2) {int m = s1.size() , n = s2.size();vector<vector<int>>dp(m+1,vector<int>(n+1));int rowsum = 0;for(int i = 0 ; i < m ; ++i){rowsum += s1[i];dp[i+1][0] = rowsum;}int colsum = 0;for(int j = 0 ; j < n ; ++j){colsum += s2[j];dp[0][j+1] = colsum;}for(int i = 1;  i <= m ; ++i){for(int j = 1;  j <= n ; ++j){ if(s1[i-1] == s2[j-1]) dp[i][j] = dp[i-1][j-1];else dp[i][j] = min(s1[i-1] + dp[i-1][j] , s2[j-1] + dp[i][j-1]);} }return dp[m][n];}
};

同时，本题还有一种做法：要使删除的ASCII最小，同时剩余的s1和s2最大，那么剩下的一定是s1和s2的最大公共子序列，那么我们只需要求出s1和s2的最大公共子序列的ASCII码值之和，然后用s1和s2的总ASCII码值和减去二倍最大公共子序列的ASCII码值之和，就得到了最小的删除和。

9 最长重复子数组

718. 最长重复子数组 - 力扣（LeetCode）

解析题目:我们需要求出两个数组的最长公共子数组。和最长公共子序列不同的是，以nums[i]为结尾的子数组，nums[i]只能跟在nums[i-1]后面，而以nums[i]为结尾的子序列的话，nums[i]可以跟在[0,i-1]的任意子序列后面。

子数组的难度是要比子序列低的，我么可以参考最长公共子序列的做法，定义状态标识如下：

dp[i][j] 表示nums1中以i位置为结尾的所有子数组，nums2中以j位置为结尾的所有子数组，最长重复子数组的长度。

状态转移方程推导：

对于dp[i][j]，由于子数组的结尾元素是固定的，所以有两种情况：

1、nums[i] == nums2[j]，那么此时是存在重复子数组的，长度至少为1，而最大的长度需要根据dp[i-1][j-1]来确定，此时 dp[i][j] = 1+ dp[i-1][j-1].

2、nums1[i] != nums2[j]，那么此时不存在以nums1[i]为结尾和以nums2[j]为结尾的重复子数组，dp[i][j] = 0;

综上，状态转移方程如下：

dp[i][j] = nums1[i] == nums2[j] ? 1 + dp[i-1][j-1] : 0;

细节问题：

初始化：由于填表时会用到 i-1 和 j-1 的位置，所以我们需要手动初始化 i = 0 和 j = 0的位置，或者可以多开一行和一列。

如果多来一行和一列，dp[i][0]表示nums1中以 i-1 为结尾的子数组和nums2中以 -1 为结尾的最长重复子数组，由于nums2的子数组是空数组，那么长度自然就是0，同理 dp[0][j] = 0,dp[0][0] = 0;

填表顺序：从上往下填写每一行，每一行从左往右填写每一列。

返回值:整个dp表的最大值。

class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {int m = nums1.size() , n = nums2.size() , res = 0;vector<vector<int>> dp(m+1,vector<int>(n+1));for(int i = 1 ; i <= m ; ++i){for(int j = 1 ; j <= n ; ++j){dp[i][j] = nums1[i-1] == nums2[j-1] ? 1 + dp[i-1][j-1] : 0;res = max(res,dp[i][j]);}}return res;}
};

总结:

两个数组的dp问题跟子数组和子序列的问题一样，我们需要根据题目意思，去研究两个数组中的特定区间的关系，再推到状态转移方程的时候，需要同时考虑两个数组的对应位置以及子区间的状态

1 最长公共子序列

2 最长回文子序列

3 不相交的线

4 不同的子序列

5 通配符匹配

6 正则表达式匹配

7 交错字符串

8 两个字符串的最小ASCII删除和

9 最长重复子数组

相关文章：