当前位置：首页 > news >正文

【算法学习】递归、搜索与回溯算法（二）

news 来源：原创 2025/8/13 12:56:10

算法学习：

https://blog.csdn.net/2301_80220607/category_12922080.html?spm=1001.2014.3001.5482

前言：

在（一）中我们挑了几个经典例题，已经对递归、搜索与回溯算法进行了初步讲解，今天我们来进一步讲解这几个算法知识点，主要是进行了一些拔高，比如引入了剪枝的操作，来看今天的例题吧

1. 经典例题

1.1 全排列 ||

1.2 组合总和

1.3 N皇后

1.4 有效的数独

1.5 单词搜索

1.6 不同路径 |||

2. 总结

1. 经典例题

1.1 全排列 ||

47. 全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],[1,2,1],[2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

1 <= nums.length <= 8
-10 <= nums[i] <= 10

算法原理：

这道题与(一)中的全排列|解法上区别不大，唯一不同的是这里需要有剪枝操作，因为全排列一中序列中的数字都不相同，这里序列中的数字是可以相同的

我们看上面这个示例，观察这个策略树发现有些分支上面画着x，这些就是错误分支，需要我们剪掉，其中橙红色的x代表的是同一个数被再次使用的错误分支，绿色的x代表的是同一层节点中相同元素被多次使用的错误分支
基于上面的剪掉错误分支的原理，我们的代码可以从两个角度切入，一个是:只关心不合法的分支;一个是:只关心合法的分支

代码实现：

class Solution {vector<vector<int>> ret;vector<int> path;bool check[10];
public:vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(),nums.end());dfs(nums);return ret;}void dfs(vector<int>& nums){if(path.size()==nums.size()){ret.push_back(path);return;}for(int i=0;i<nums.size();i++){//只关注不合法的分支，当是不合法的分支时，需要剪掉，所以不进入递归if(check[i]==true||(i!=0&&nums[i]==nums[i-1]&&check[i-1]==false))continue;//只关注合法的分支的做法就是将上面if中的条件相反，然后把下面的内容包在函数体内path.push_back(nums[i]);check[i]=true;dfs(nums);path.pop_back();check[i]=false;}}
};

`1.2 组合总和`

LCR 081. 组合总和

给定一个无重复元素的正整数数组 candidates 和一个正整数 target ，找出 candidates 中所有可以使数字和为目标数 target 的唯一组合。

candidates 中的数字可以无限制重复被选取。如果至少一个所选数字数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的唯一组合数少于 150 个。

示例 1：

输入: candidates = [2,3,6,7], target = 7<
输出: [[7],[2,2,3]]

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

示例 4：

输入: candidates = [1], target = 1
输出: [[1]]

示例 5：

输入: candidates = [1], target = 2
输出: [[1,1]]

提示：

1 <= candidates.length <= 30
1 <= candidates[i] <= 200
candidate 中的每个元素都是独一无二的。
1 <= target <= 500

算法原理：

代码实现：

class Solution {vector<vector<int>> ret;vector<int> path;int sum;
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {dfs(candidates,target,0);return ret;}void dfs(vector<int>& candidates,int target,int pos){if(sum>=target){if(sum==target) ret.push_back(path);return;}for(int i=pos;i<candidates.size();i++){sum+=candidates[i];path.push_back(candidates[i]);dfs(candidates,target,i);path.pop_back();sum-=candidates[i];}}
};

1.3 N皇后

51. N 皇后

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

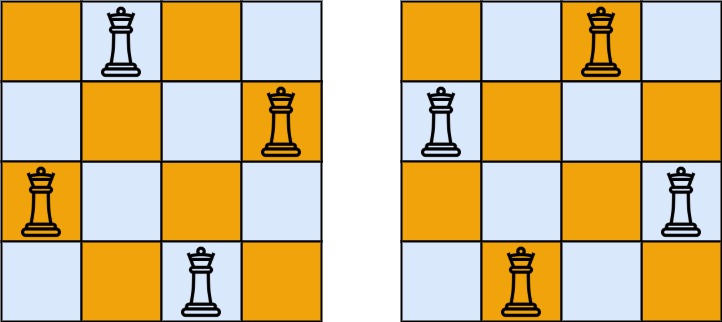
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

提示：

1 <= n <= 9

算法原理：

解释:

这道题最关键的就是我们上面的剪枝操作，根据题意我们知道在一个nxn棋盘中，一个列中只能存在一个元素，所以我们可以创建一个bool数组col来标记列的元素情况我们把棋盘抽象到坐标系上，因为对角线上也只能有一个元素，对角线可以有如图的两种，这两种它们x+y都是一个定值，所以也可以创建bool数组来对它们进行标记

y-x可能为负数，负数不能作为bool数组的下标，所以可以加上一个n的偏移量

代码实现：

class Solution {bool checkCol[10],checkDigal1[20],checkDigal2[20];vector<vector<string>> ret;vector<string> path;int n;
public:vector<vector<string>> solveNQueens(int _n) {n=_n;path.resize(n);for(int i=0;i<n;i++)path[i].append(n,'.');dfs(0);return ret;}void dfs(int row){if(row==n){ret.push_back(path);return;}for(int col=0;col<n;col++)    //尝试在这一行放置皇后{//剪枝if(!checkCol[col]&&!checkDigal1[row-col+n]&&!checkDigal2[row+col]){path[row][col]='Q';checkCol[col]=checkDigal1[row-col+n]=checkDigal2[row+col]=true;dfs(row+1);//恢复现场path[row][col]='.';checkCol[col]=checkDigal1[row-col+n]=checkDigal2[row+col]=false;}}}
};

1.4 有效的数独

36. 有效的数独

请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

注意：

一个有效的数独（部分已被填充）不一定是可解的。
只需要根据以上规则，验证已经填入的数字是否有效即可。
空白格用 '.' 表示。

示例 1：

输入：board = 
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：true

示例 2：

输入：board = 
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：false
解释：除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的

提示：

board.length == 9
board[i].length == 9
board[i][j] 是一位数字（1-9）或者 '.'

算法原理：

解释:

这题不是回溯类的题，但是通过这题我们可以更好的理解N皇后那道题，这道题也是要保证数据在一定位置上不能重复出现，所以都可以采取哈希的方式(这里的数组模拟的就是哈希)进行标记，这道题要求同一行、同一列和同一个九宫格中都不能出现相同的方式所以我们就可以用三个bool数组来进行标记，我们拿第一个row[9][10]来举例，这表示的就是第i行0~9每个数字的存在情况，需要注意的是第三个数组，它用来标记每个九宫格里数字的出现情况，所以我们把整个大表格分为3x3九份，同时后面的【10】是用来记录各个数字出现情况，而且grid数组对应的下标其实就是【x/3】【y/3】

代码实现：

class Solution {bool col[9][10];bool row[9][10];bool grid[3][3][10];
public:bool isValidSudoku(vector<vector<char>>& board) {for(int i=0;i<9;i++){for(int j=0;j<9;j++){if(board[i][j]>='0'&&board[i][j]<='9'){int num=board[i][j]-'0';if(row[i][num] ||col[j][num]||grid[i/3][j/3][num]) return false;row[i][num]=col[j][num]=grid[i/3][j/3][num]=true;}}}return true;}
};

1.5 单词搜索

79. 单词搜索

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

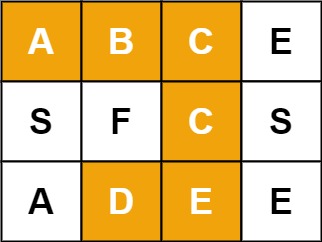
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2：

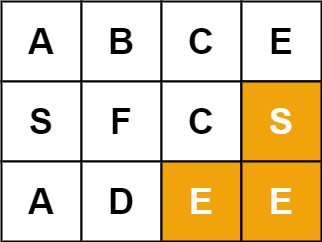
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出：true

示例 3：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出：false

提示：

m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board 和 word 仅由大小写英文字母组成

算法原理：

代码实现：

class Solution {bool vis[7][7];int m,n;
public:bool exist(vector<vector<char>>& board, string word) {m=board.size(),n=board[0].size();for(int i=0;i<m;i++)for(int j=0;j<n;j++){if(board[i][j]==word[0]){vis[i][j]=true;if(dfs(board,i,j,word,1)) return true;vis[i][j]=false;}}return false;}int dx[4]={0,0,1,-1},dy[4]={1,-1,0,0};bool dfs(vector<vector<char>>& board,int i,int j,string& word,int pos){if(pos==word.size()) return true;for(int k=0;k<4;k++){int x=i+dx[k], y=j+dy[k];if(x>=0 && x<m &&y>=0 &&y<n &&board[x][y]==word[pos] &&vis[x][y]==false){vis[x][y]=true;if(dfs(board,x,y,word,pos+1)) return true;vis[x][y]=false;}}return false;}
};

1.6 不同路径 |||

980. 不同路径 III

在二维网格 grid 上，有 4 种类型的方格：

1 表示起始方格。且只有一个起始方格。
2 表示结束方格，且只有一个结束方格。
0 表示我们可以走过的空方格。
-1 表示我们无法跨越的障碍。

返回在四个方向（上、下、左、右）上行走时，从起始方格到结束方格的不同路径的数目。

每一个无障碍方格都要通过一次，但是一条路径中不能重复通过同一个方格。

示例 1：

输入：[[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
输出：2
解释：我们有以下两条路径：
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)

示例 2：

输入：[[1,0,0,0],[0,0,0,0],[0,0,0,2]]
输出：4
解释：我们有以下四条路径： 
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)

示例 3：

输入：[[0,1],[2,0]]
输出：0
解释：
没有一条路能完全穿过每一个空的方格一次。
请注意，起始和结束方格可以位于网格中的任意位置。

提示：

1 <= grid.length * grid[0].length <= 20

这道题可以用动归来解决，但是难度比较大，用爆搜简单一点

这道题原理之类与前面几题很相似，我们把思路搞明白就很容易上手，根据题意，我们要做的是从1出发，遍历所有的0，然后到达2
我们可以把所有能够到达2的路径都尝试一遍，其中许多路径肯定是没有把0全部遍历的，这种的就需要被剪掉，我们可以采取一种更简单的方式，我们可以定义一个常量count用来记录我们所走过的0的个数，然后当我们走到终点时判断一下我们所走的0的个数与整个表格中0的个数是否一样，一样就代表我们把所有的0都遍历过了

代码实现：

class Solution {int dx[4]={1,-1,0,0};int dy[4]={0,0,-1,1};int step=0;int m,n;int ret=0;bool vis[20][20];
public:int uniquePathsIII(vector<vector<int>>& grid) {m=grid.size(),n=grid[0].size();int bx=0,by=0;for(int i=0;i<m;i++)for(int j=0;j<n;j++){if(grid[i][j]==0) step++;else if(grid[i][j]==1) bx=i,by=j;}step+=2;vis[bx][by]=true;dfs(grid,bx,by,1);return ret;}void dfs(vector<vector<int>>& grid,int i,int j,int path){if(grid[i][j]==2){if(step==path)ret++;return;}for(int k=0;k<4;k++){int x=i+dx[k],y=j+dy[k];if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]!=-1&&vis[x][y]==false){vis[x][y]=true;dfs(grid,x,y,path+1);vis[x][y]=false;}}}
};

2. 总结

上一篇主要讲解的是递归、搜索与回溯算法的一些基本知识和简单例题，本篇的一些题型结合深搜和宽搜的知识，还要用到一些剪枝的操作，总体来说难度大了很多，需要花费更多的时间在上面

本篇笔记：

感谢各位大佬观看，创作不易，还望各位大佬点赞支持！！

1. 经典例题

1.1 全排列 ||

1.2 组合总和

1.3 N皇后

1.4 有效的数独

1.5 单词搜索

1.6 不同路径 |||

2. 总结

相关文章：

`1.2 组合总和`