当前位置：首页 > news >正文

FOC算法开环控制基础

news 来源：原创 2025/8/22 15:05:56

1. 为什么要有FOC算法

先看看从有刷电机到无刷电机的简单介绍，如下图1，通电螺线圈会产生磁场，这个磁场会产生N级和S级，然后这个电磁铁就可以吸引永磁体，S级吸引N级，N级吸引S级，通俗的来说，电机的原理就是固定其中一个来让另一个旋转，固定永磁体，让电磁铁旋转或者固定电磁铁，让永磁体旋转，转的那个东西叫转子，不转的那个东西叫定子，不管哪种情况都需要使电磁铁的磁极周期性的翻转，这样就会使产生的磁场方向也翻转，周而复始电机就诞生了，具体的物理图以及更深层次的东西就不在这里说了。
在这里插入图片描述
图1 电磁铁驱动永磁体

如果永磁体做定子，电磁铁做转子，因为电磁铁需要连接导线，所以要让电磁铁旋转的话必须得解决导线的问题，同时还能让电流反向，如下图2，这个电刷起到了导线的作用，同时由于转子的结构特点，随着转子的旋转，作为转子的电磁铁产生的磁场方向也在变化，由于这个电刷的存在，所以这中电机叫做直流有刷电机。所以这种电机被称为有刷电机，
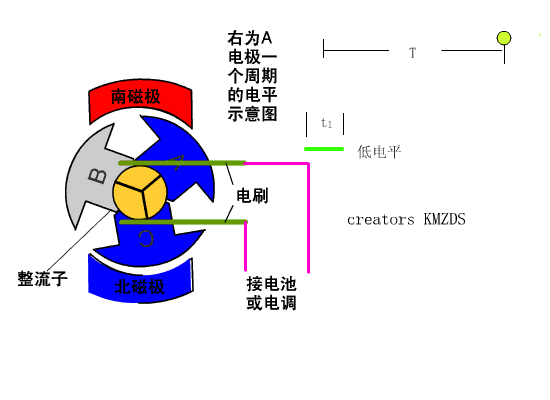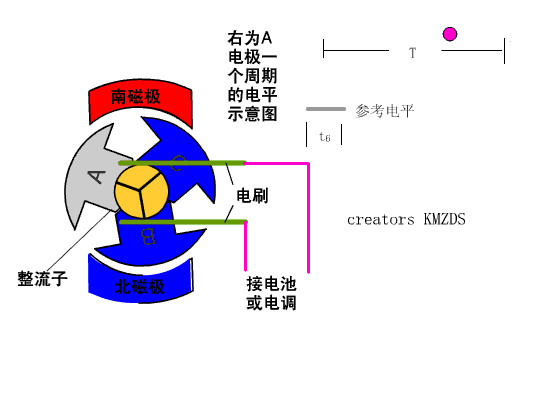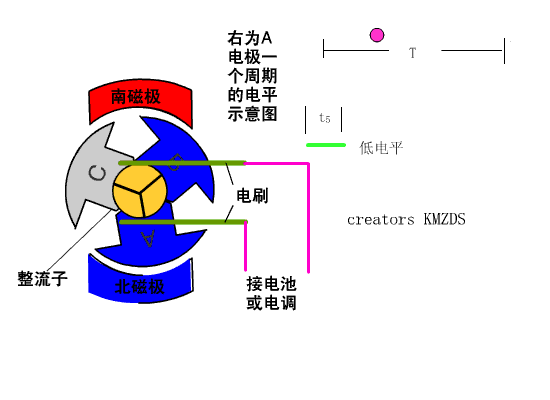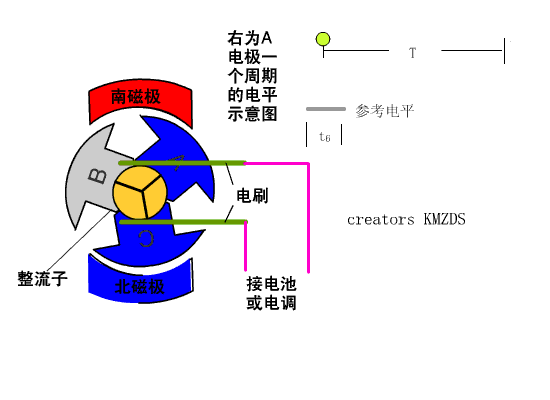
请添加图片描述
图2 直流有刷电机

如果永磁体做转子，电磁铁做定子，如下图3，那就要使得施加在电磁铁上的电压遵循一定的规律，从而产生周期变化的磁场来驱动作为转子的永磁体转动，产生符合条件的电压的算法之一就是FOC算法。
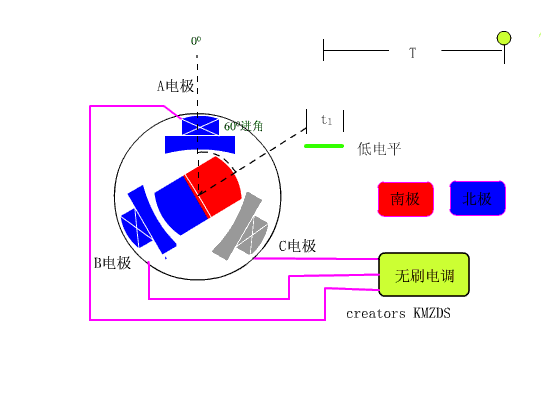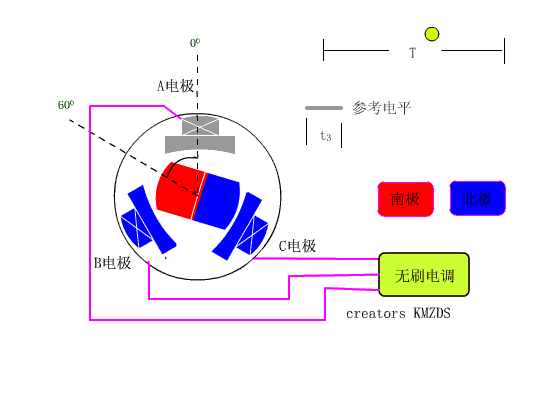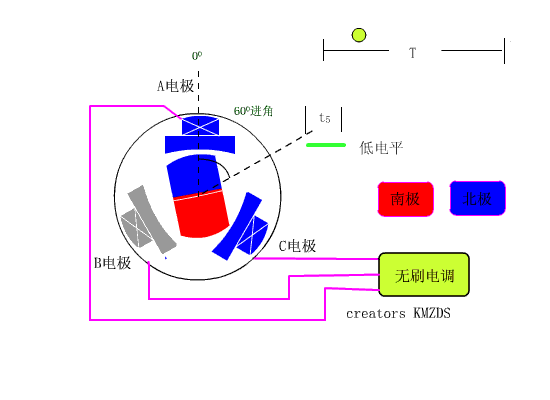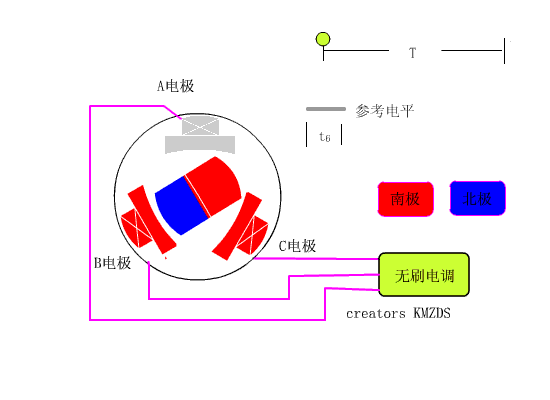
请添加图片描述
图2 直流无刷电机
具体的转动原理去参考网上的其他资料，我这里写的太粗糙了。

2. FOC基本原理

请添加图片描述
图3 FOC算法流程图
FOC算法的简要流程就是上图这样的，要想控制电机旋转就需要给电机输入旋转的参数，就是电机的转矩，然后通过两个变换来转换为电机的三相输入信号，可以是输入的电压，也可以是输入的电流，称为相电压和相电流，相电压等于相电流乘以相电阻，所以二者是完全的正比例关系，可以相互转换，后面所有的公式变换对于这个电流和电压都是完全相同的，公式推导时使用电流，考虑物理意义时根据情况选择，所以实际的情况是一个反着来的过程，要想确定输入给电机的信号就需要根据输入的三路信号反推出输入给它的信号，然后由这个信号进一步推出应该输入什么样的转矩，所以核心就是这两个变换，下面开始介绍这两个变换。

2.1 克拉克变换

2.1.1 克拉克变换的推导

根据上面的图2可以知道要想实现无刷电机的转动控制需要确定三路的输入电流，也就是无刷电机的三相电控制，要表达每一路的电压或者电流需要三个方程，而无刷电机定子有三个绕组(即使不是三个也可以简化为三个)，每个绕组发出一个相电压。由于这三个绕组在位置上等分了一个圆周，即彼此相差 $2\pi/3$ ，导致三相电压的幅度变化不一致，而是存在一个延时，这个延时是旋转1/3圆周的时间，也就是说三相电相互之间的相位差相差 $2\pi/3$ ，从物理学的角度来看，整个系统的自由度就是2，所以方程就可以简化为2个，而电机转动的时候均匀的，所以三相电流之间的幅值和频率是相同的，所以假设三相电流的定义如下:
$\begin{cases} i_a = i_{max}cos(wt)\\ i_b = i_{max}cos(wt+\frac{2\pi}{3}) \\ i_c = i_{max}cos(wt-\frac{2\pi}{3}) \end{cases}$
在电机定子上建立实轴平行于 $i_a$ 的复数坐标系， $i_a，i_b，i_c$ 三者夹角为 $\frac{2\pi}{3}$ ， $i_a$ 没有变化， $i_b$ 变为 $i_be^{\frac{2\pi j}{3}}$ ， $i_c$ 变为 $i_ce^{\frac{-2\pi j}{3}}$ （Tips：对一个复数乘以 $e^{j\theta}$ 表示将这个复数表示的向量旋转 $\theta$ 度， $\theta$ 为正表示逆时针旋转， $\theta$ 为负表示顺时针旋转），将三者分别投影到实轴( $\alpha$ 轴)和虚轴( $\beta$ 轴)以后并相加可以得到下面的结果：
$\begin{cases} i_\alpha = i_a + i_b \cos\left(\frac{2\pi}{3}\right) + i_c \cos\left(-\frac{2\pi}{3}\right) = i_a - \frac{1}{2}(i_b + i_c) \\ i_\beta = i_b \sin\left(\frac{2\pi}{3}\right) + i_c \sin\left(-\frac{2\pi}{3}\right) = \frac{\sqrt{3}}{2}(i_b - i_c) \end{cases}$
用矩阵的形式写出来就是下面这样：
$\begin{bmatrix} i_\alpha \\ i_\beta \end{bmatrix} = \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \begin{bmatrix} i_a \\ i_b \\ i_c \end{bmatrix}$
这个变换就叫克拉克变换，所以克拉克变换的数学本质就是将三个复数向量合并成为一个，实部和虚部分开运算的转换矩阵就是克拉克变换，物理本质就是将三相的电流或电压降维变成二维，转换前后的结果都是随时间变化的。

2.1.2 等幅值克拉克变换

将前面的三路电流相加并化简可得：
$i_{\Sigma} = i_a+i_b+i_c = \frac{3}{2}i_{max}e^{-jwt}$
可以看出克拉克变换前后的电流幅值变大了，成了原来的 $\frac32$ 倍，为了方便处理，需要让 $i_a$ 和 $i_\alpha$ 在变换前后相同，所以 $i_{max}$ 要变为原来的 $\frac23$ ， $i_{max}$ 变了意味着三路电流都需要变为原来的 $\frac23$ ，所以等幅值的克拉克变换形式就是下面这样，多了个系数 $\frac23$ 。
$\begin{bmatrix} i_\alpha \\ i_\beta \end{bmatrix} = \frac23\begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \begin{bmatrix} i_a \\ i_b \\ i_c \end{bmatrix}$
把基尔霍夫定律代入等式右边就可以进一步化简等幅值克拉克变换：
$\begin{bmatrix} i_\alpha \\ i_\beta \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ \frac{1}{\sqrt{3}} & \frac{2}{\sqrt{3}} \end{bmatrix} \begin{bmatrix} i_a \\ i_b \end{bmatrix}$
这个系数矩阵的行列式值是 $\frac{2}{\sqrt{3}}$ ，所以这是一个满秩矩阵，所以这个系数矩阵的逆矩阵就是克拉克逆变换矩阵，完整的克拉克逆变换如下：
$\begin{bmatrix} i_a \\ i_b \end{bmatrix} =\begin{bmatrix} 1 & 0 \\ -\frac{1}{2} & \frac{\sqrt{3}}{2} \end{bmatrix} \begin{bmatrix} i_\alpha \\ i_\beta \end{bmatrix}$
$i_c$ 的计算可以通过 $i_a$ ， $i_b$ 和基尔霍夫电流定律得到。

2.2 帕克变换

正如前面克拉克变换结束的时候所说，克拉克变换前后的电压和电流都是随着时间变化的，我们要想控制电机必须在合适的时间给合适的电压，对于高频变化的信号很显然是很不方便的，甚至是不现实的，所以我们需要想办法把我们的控制参数中的时间给去掉，这样对于后续处理就会方便很多，在高中物理学过正弦交流电的发电原理，发电机发出的正弦交流电 $U=A\sin(wt+\varphi)$ 的角频率 $w$ 和发电机转子的角速度是正比例的，比例系数是极对数除以2，所以在这里我们也可以合理的猜测对于极对数为1的电机转动的角速度与正弦电压的角频率是相同的，同时考虑到角速度的公式 $w=\frac{\mathrm{d}\theta}{\mathrm{d}t}$ ，可以在转子上建立局地坐标系， $\mathrm{d}$ 轴方向与转子内磁场方向重合，纵坐标 $\mathrm{q}$ 轴垂直于 $\mathrm{d}$ 轴，符合右手螺旋定则，如下图所示，克拉克变换的前后坐标系是绝对坐标系，也就是说固定在转子上的这个坐标系是相对于绝对坐标系旋转的。
在这里插入图片描述
当电机转过的角度为 $\theta$ 的时候，克拉克逆变换后得到是一个复数 $i_{\alpha\beta}=i_{max}e^{-jwt}$ ，这个复数在转子坐标系下的极角应该比原本的定子坐标系的极角小 $\theta$ ，所以转子坐标系的极角应该是定子坐标系的极角减去 $\theta$ ，所以 $i_{\mathrm{d}\mathrm{q}}=i_{max}e^{-j(wt+\theta)}$ ，将他们分别在实轴和虚轴展开可得：
$\begin{cases} i_\alpha =i_{max}cos(wt) \\ i_\beta = -i_{max}sin(wt)\\ i_\mathrm{d} =i_{max}cos(wt+\theta) \\ i_\mathrm{q}= -i_{max}sin(wt+\theta) \end{cases}$
然后利用余弦的和角公式将后两个式子展开，将前两个代入就可以得到如下变换(已转换为矩阵形式)：
$\begin{bmatrix} i_\mathrm{d} \\ i_\mathrm{q} \end{bmatrix} =\begin{bmatrix} \mathrm{cos}\theta & \mathrm{sin}\theta \\ -\mathrm{sin}\theta & \mathrm{cos}\theta \end{bmatrix} \begin{bmatrix} i_\alpha \\ i_\beta \end{bmatrix}$
这个矩阵的行列式的值等于1，所以这是一个全等变换，(说句题外话，全等变换有对称，平移和旋转，这里就是旋转，这个转换矩阵就叫做帕克变换，实际上这个矩阵在数学，物理和工程领域的应用数不胜数，遍地都是它的例子)，可以注意到帕克变换后的电流分量一个平行于转子转动方向 $\mathrm{q}$ ，一个平行于转子转动方向 $\mathrm{d}$ ，这样问题就简单很多了。 $\theta$ 可以通过编码器实时测量得到，这样我们通过控制 $i_{\mathrm{q}}$ 和 $i_{\mathrm{d}}$ 就可以控制定子产生的磁场。安培力表示通电导线在磁场的受力情况，表达式是 $F=BILsin\theta$ ， $\theta$ 是电流和磁场的夹角，所以 $\theta=\frac{\pi}{2}$ 的时候导线受力最大，在这里就是转子提供的转矩最大，所以一般设置 $i_{\mathrm{d}}=0$ ，只需要设置 $i_{\mathrm{q}}$ 就可以决定电机三相电流的大小，所以我们实际应用需要的是帕克逆变换，根据 $i_{\mathrm{q}}$ 和 $i_{\mathrm{d}}$ 来计算 $i_{\mathrm{\alpha}}$ 和 $i_{\mathrm{\beta}}$ ，帕克逆变换如下：
$\begin{bmatrix} i_\alpha \\ i_\beta \end{bmatrix} =\begin{bmatrix} \mathrm{cos}\theta & -\mathrm{sin}\theta \\ \mathrm{sin}\theta & \mathrm{cos}\theta \end{bmatrix} \begin{bmatrix} i_\mathrm{d} \\ i_\mathrm{q} \end{bmatrix}$

2.3 FOC算法基本原理总结

所谓FOC的过程，就是输入需求的电机力矩，最后得到对应的真实世界电机输出力矩的过程，如下图所示。而其中最核心的数学过程，就是帕克逆变换和克拉克逆变换，而这两个变换的数学公式就是下图中框图上面的公式，其中帕克变换可以对用户输入的 $i_{q}$ 进行变换，根据电角度算出 $i_\alpha$ 和 $i_\beta$ ，接着，通过克拉克逆变换，求出三相电流 $i_a, i_b, i_c$ ，最后 $i_a, i_b, i_c$ 能够用作控制指令输入到电机控制器硬件中进行电机的控制。
在这里插入图片描述
在通过 $i_q$ 得到 $i_a, i_b, i_c$ 让电机顺利转起来以后还需要进行调节，经过这一系列的过程以后电机的实际工作情况是否和我们预期的一样是不知道的，所以需要对电机的电流，速度和位置数据进行采集，然后通过PID控制将预设值对实际值进行动态调节，让电机的实际运动与预期相同。

3. FOC闭环控制

下面是PID算法的基本表达式，也是FOC闭环控制的理论基础
$k_pe(t)+k_i\int_{0}^{t}e(\tau)\mathrm{d}\tau+k_d\frac{\mathrm{d}e(t)}{\mathrm{d}t}$
对应的离散形式是这样的：
$k_pe(t)+k_i\sum_{j=0}^{t}e(j)+k_d[e(t)-e(t-1)]$
三项的基本含义如下：

比例项直接反映当前误差的实时大小，通过比例系数 $k_p$ 对误差进行放大或缩小，快速调整控制量以减少偏差。例如，若当前误差较大，比例项会立即输出较强的控制信号以缩小误差。比例项能迅速减小误差，但对稳态误差（静差）无法完全消除；
积分项通过积分常数 $T_i$ ( $k_i = \frac{k_pT}{Ti}$ ，T为采样周期)累积历史误差，消除比例控制无法处理的稳态误差。例如，若误差长期存在，积分项会持续累积误差值并增强控制作用，直至误差归零。积分项的主要作用就是彻底消除系统稳态误差；
微分项通过微分常数 $T_d$ ( $k_d = \frac{k_pT_d}{T}$ ，T为采样周期)预测误差的变化趋势（即误差的导数），提前抑制超调并加快系统响应速度。例如，若误差快速增大，微分项会提前输出反向控制量以减缓变化速度。微分项住主要特点有抑制超调：微分作用可提高系统阻尼，减少超调量和调节时间。噪声敏感：微分对高频噪声敏感，可能放大干扰信号，需配合滤波措施。

3.1 FOC位置闭环

3.2 FOC速度闭环

3.3 FOC电流闭环

4. 参考资料

https://dengfoc.com/
https://www.bilibili.com/video/BV1cj411M7Xu
https://blog.csdn.net/lanxiaoke123/article/details/90410560
https://blog.csdn.net/weixin_42164589/article/details/95330403