6.10.单源最短路径问题-Dijkstra算法

一.BFS算法的局限性:

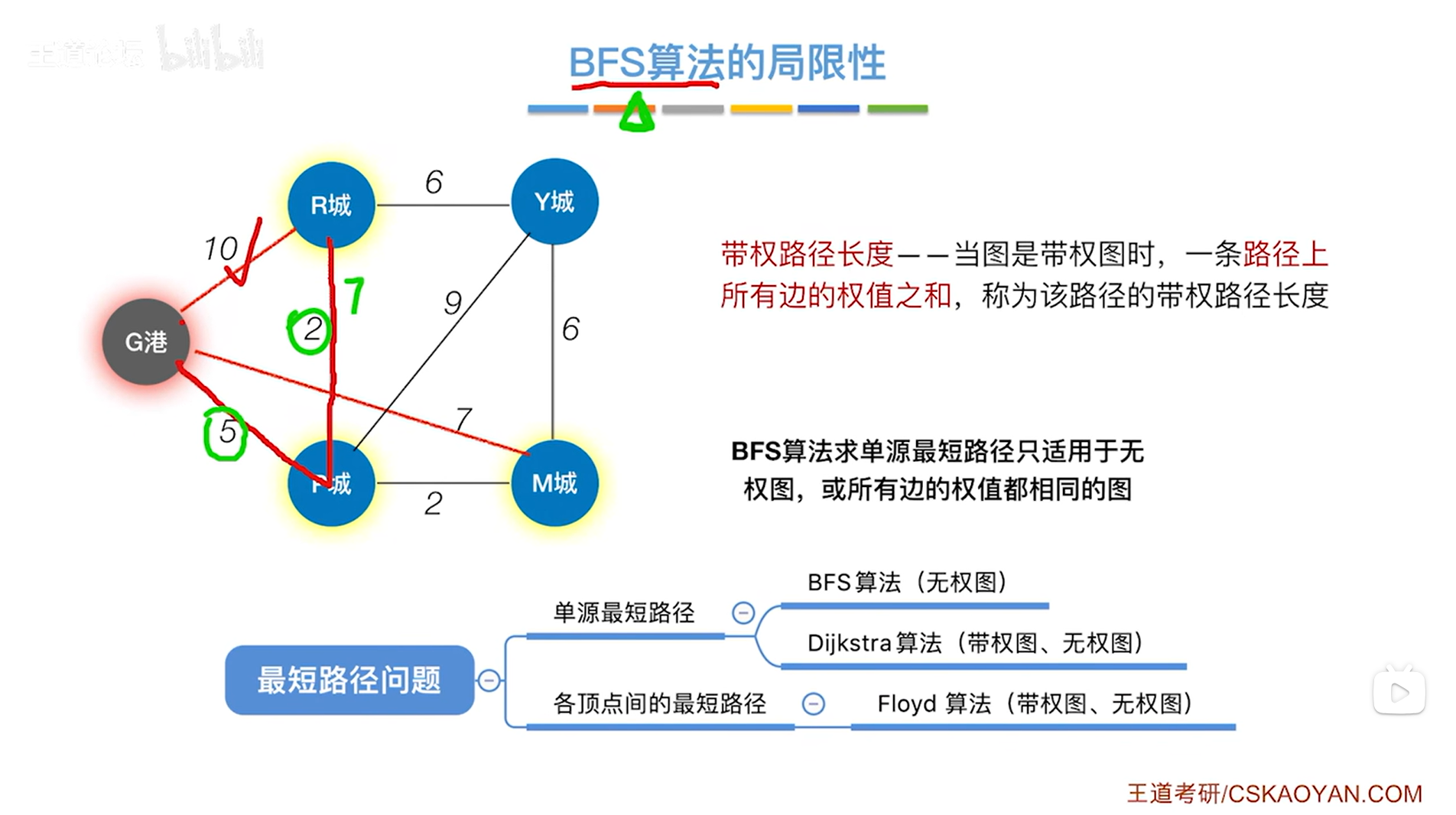
如上图,BFS算法可以解决无权图的单源最短路径问题,
如果是解决带权图的单源最短路径问题,BFS算法就不适用了,如下图:

如上图,比如求G港到其他顶点的最短路径,
按照BFS算法,找到的G港到R城的最短路径就是从G港直接到R城的这条边即权值为10的边,因为G港的邻接顶点有一个R城,如下图:

如上图,实际上从G港到R城有一条更短的路径,就是G港->P城->R城,路径总长度只有7,
但如果按照BFS算法的话,R城就不会被第二次访问,也就不会得出G港->P城->R城这条更短的路径,如下图:

如上图,因此BFS算法不适用于带权图的单源最短路径问题,带权图的单源最短路径就需要用到Dijkstra算法,如下图:

二.回顾:带权路径长度->本章把带权路径长度简称为路径长度
三.Dijkstra算法:
1.前言:

以上述图片为例来解释Dijkstra算法,其中的图是有向图,
之所以不使用无向图,是因为无向图与有向图的原理一致,无向图的一条无向边就对应有向图的两条有向边,
因此解决了有向图的问题,无向图的问题也就迎刃而解了,如下图:


2.实例:

以上述图片的有向图为例,假设找出从顶点v0到达其他顶点的最短路径,如下图:

如上图,需要初始化三个数组final、dist、path(这3个数组中数据的内容都依次对应v0顶点、v1顶点、v2顶点、v3顶点、v4顶点)->
1.final数组表示目前为止是否找到从起点v0出发到达其他顶点的最短路径:
对于v0顶点,v0顶点对应的final值初始化为true,因为起点是v0,从起点v0到v0的最短路径就是0,意味着一开始就可以确定到达v0的最短路径,
对于v1、v2、v3、v4顶点,v1、v2、v3、v4对应的final值都初始化为false,因为一开始都无法确定从起点v0出发到达这些顶点的最短路径;
2.dist数组表示目前为止能够找到的最短路径的总长度:
对于v0顶点,起点v0到v0的最短路径长度为0,因此v0对应的dist数组的值为0,
对于v1顶点,一开始能找到一条v0直达v1的边,所以目前来看v0到v1的最短路径是10,因此v1对应的dist数组的值为10,
对于v4顶点,一开始能找到一条v0直达v4的边,所以目前来看v0到v4的最短路径是5,因此v4对应的dist数组的值为5,
对于v2和v3顶点,v2顶点和v3顶点并不存在从v0顶点直达的路径,所以把v2、v3对应的dist数组的值都初始化为无穷,表示目前还没有找到能够通往v2和v3的最短路径;
3.path数组用于记录每一个顶点在最短路径上的直接前驱:
对于v0顶点,v0顶点对于起点v0而言不存在最短路径,也就不存在直接前驱,所以v0对应的path值为-1,
对于v1顶点,目前能够确定的从起点v0到达v1的最短路径就是从v0直达v1,因此v1对应的path值初始化为0(0就是v0在path数组里的索引),
对于v4顶点,目前能够确定的从起点v0到达v4的最短路径就是从v0直达v4,因此v4对应的path值初始化为0,
对于v2和v3顶点,v0到达v2、v3顶点还没有相关的最短路径,因此也就没有直接前驱,所以v2、v3对应的path值都初始化为-1;
如下图:

如下图,开始第一轮的处理:

如上图,循环遍历三个数组final、dist、path全部的信息,从中找到还没确定最短路径的顶点即对应的final值为false、dist值最小的顶点,
显然在final值为false、dist值最小的顶点中找到的是v4顶点,开始处理v4顶点,
此时把v4顶点对应的final值设为true,表示现在已经可以确定对于v4顶点来说,从起点v0到v4的最短路径长度就是5,并且它的直接前驱是0索引上的顶点即v0,因此就确定了v0到v4的最短路径,
(这里之所以能确定从起点v0到v4的最短路径就是v0->v4且长度是5,是因为起点v0只指向v1和v4,如果不直接达到v4而是经过v1再到达v4,那么一定会经过v0到v1之间权值为10的边,10已经比v0直达v4之间的边的权值5大了,因此经过v1再到达v4显然不是最短路径,那么从v0直达v4就是最短路径)
如下图:

如上图,还需要继续检查v4指向的顶点即v1、v2、v3,最后只会修改对应的final值为false即目前还没有确定最短路径的顶点的dist和path信息,因此需要修改v1、v2、v3顶点对应的dist和path信息,
此时就需要检查到达v1、v2、v3,如果经过v4的话,那么有没有可能在之前找到的路径外存在更短的路径呢?
对于v1,在之前找到的路径中从v0到达v1的比较好的一条路径是长度为10,路径信息是v0->v1,但现在可以确定从起点v0到v4有一条长度为5的路径,而从v4到v1有一条长度为3的路径,因此如果v1顶点是v0->v4->v1过来的话,那么就可以找到一条总长度为5加3即8的路径,这条路径显然要比刚开始找到的长度为10的路径更好,所以要把v1对应的dist值修改为8,同时把v1对应的path值修改为4即前驱是v4(v4在path数组中的索引为4);
对于v2,之前就没有找到能够从v0直达v2的路径,但是现在如果经过v4再到达v2的话,那么就可以找到一条总长度为5加9即14的路径,路径信息为v0->v4->v2,所以要把v2对应的dist值修改为14,同时把v2对应的path值修改为4即前驱是v4(v4在path数组中的索引为4);
对于v3,之前就没有找到能够从v0直达v3的路径,但是现在如果经过v4再到达v3的话,那么就可以找到一条总长度为5加2即7的路径,路径信息为v0->v4->v3,所以要把v3对应的dist值修改为7,同时把v3对应的path值修改为4即前驱是v4(v4在path数组中的索引为4);
如下图:

如下图,开始第二轮的处理:
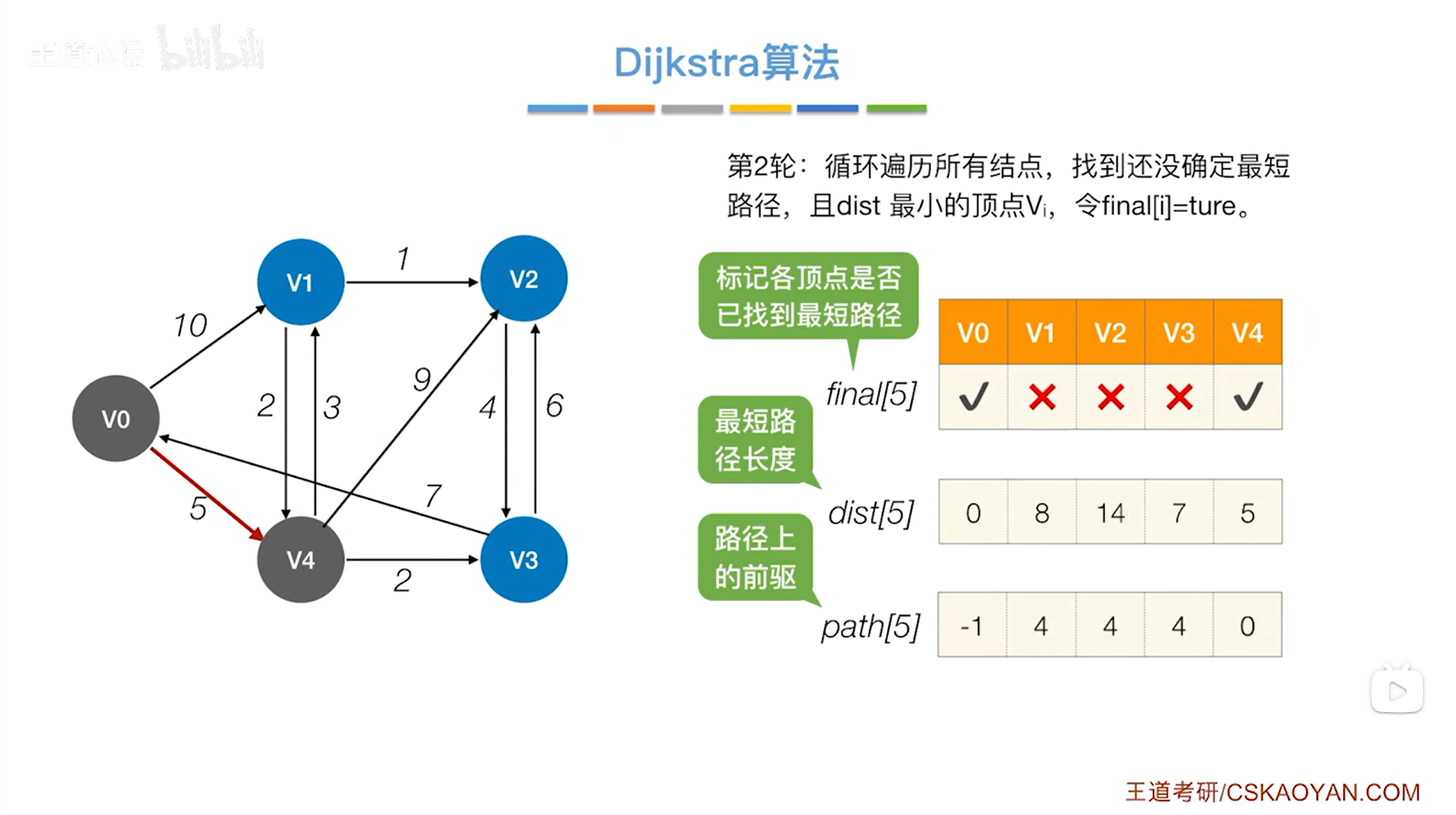
如上图,循环遍历三个数组final、dist、path全部的信息,从中找到还没确定最短路径的顶点即对应的final值为false、dist值最小的顶点,
显然在final值为false、dist值最小的顶点中找到的是v3顶点,开始处理v3顶点,
此时把v3顶点对应的final值设为true,表示现在已经可以确定对于v3顶点来说,从起点v0到v3的最短路径长度就是7,并且它的直接前驱是4索引上的顶点即v4,因此就确定了v0到v3的最短路径,
(这里之所以能确定从起点v0到v3的最短路径就是v0->v4->v3且长度是7,是因为直达v3的顶点只有v4和v2,从起点v0出发,到达v4的成本要比v2小,因此从v4到v3比从v2到v3更好,从起点v0到v4的最短路径是v0->v4,因此从起点v0到v3的最短路径为v0->v4->v3)
如下图:
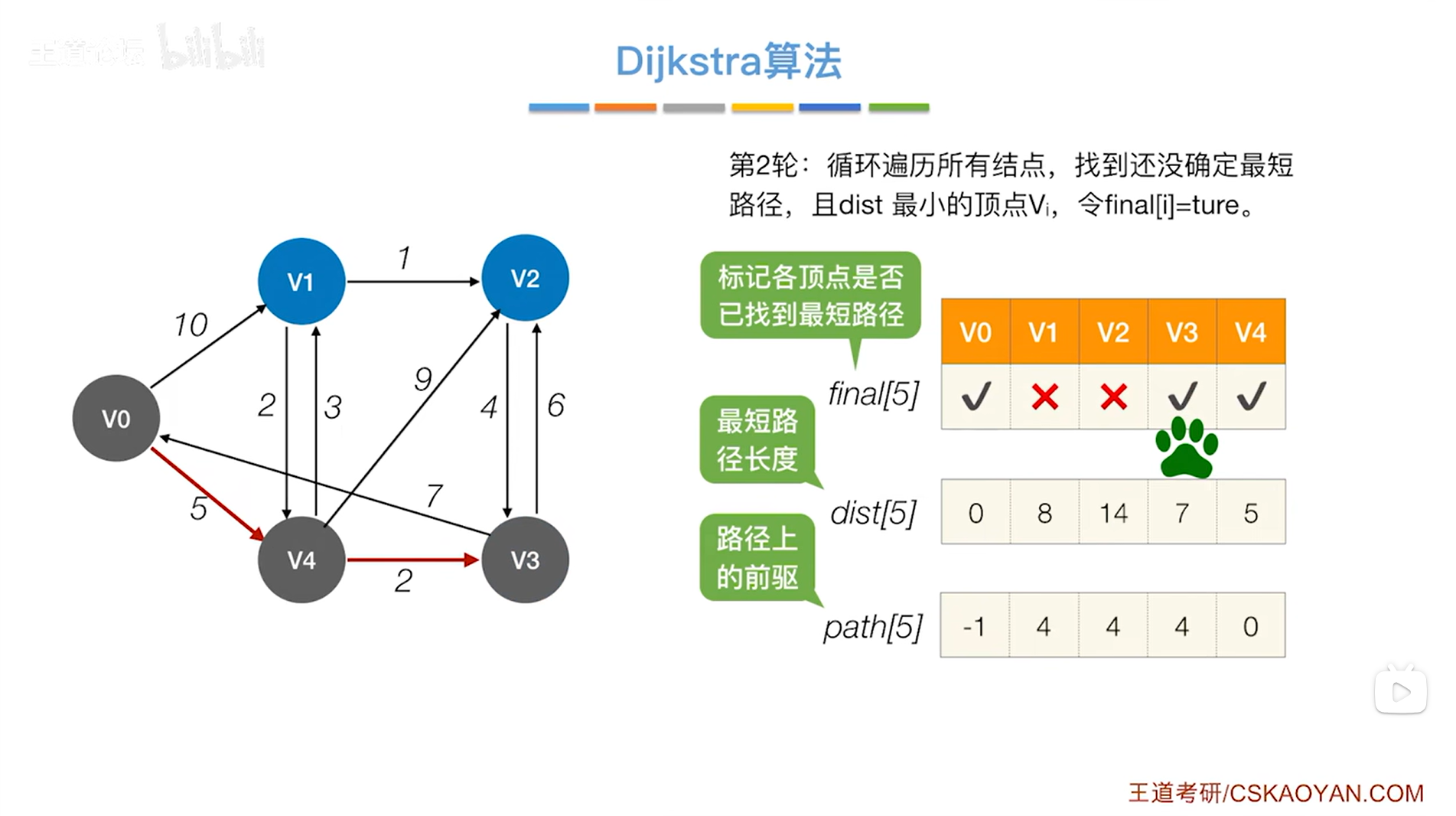
如上图,还需要继续检查v3指向的顶点即v0、v2,最后只会修改对应的final值为false即目前还没有确定最短路径的顶点的dist和path信息,因此需要修改v2顶点对应的dist和path信息,
此时就需要检查到达v2,如果经过v3的话,那么有没有可能在之前找到的路径外存在更短的路径呢?
对于v2,之前找到的从v0到达v2的最短路径长度为14,路径信息是v0->v4->v2,该路径最终是从v4直达v2的,但是现在如果从v3直达v2,那么就可以找到一条总长度为5加2加6即13的路径,路径信息是v0->v4->v3->v2,这个路径显然比v0->v4->v2更优秀(因为路径总长度更短),所以要把v2对应的dist值修改为13,同时把v2对应的path值修改为3即前驱是v3(v3在path数组中的索引为3);
如下图:

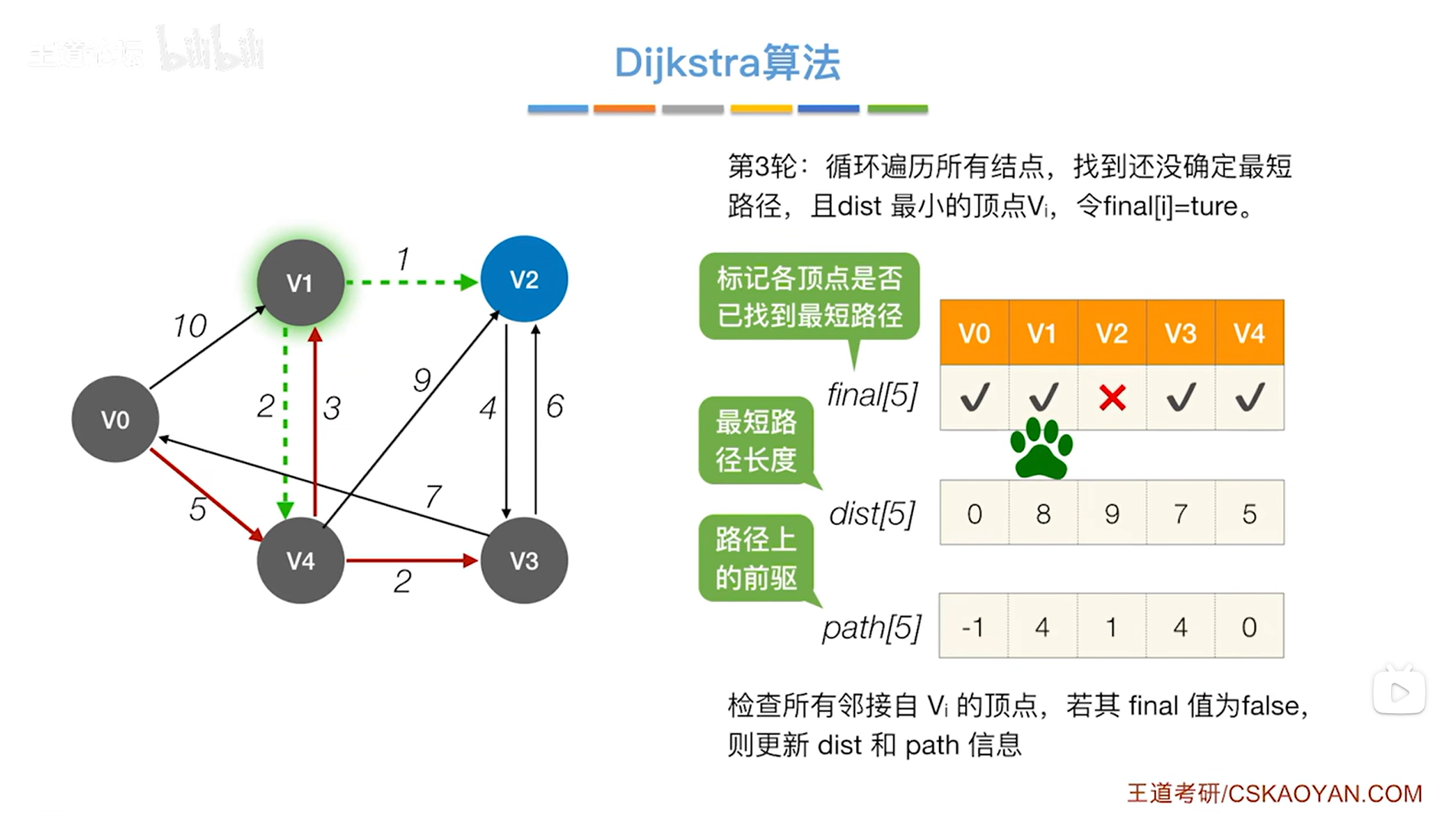
如下图,开始第三轮的处理:

如上图,循环遍历三个数组final、dist、path全部的信息,从中找到还没确定最短路径的顶点即对应的final值为false、dist值最小的顶点,
显然在final值为false、dist值最小的顶点中找到的是v1顶点,开始处理v1顶点,
此时把v1顶点对应的final值设为true,表示现在已经可以确定对于v1顶点来说,从起点v0到v1的最短路径长度就是8,并且它的直接前驱是4索引上的顶点即v4,因此就确定了v0到v1的最短路径,
(这里之所以能确定从起点v0到v1的最短路径就是v0->v4->v1且长度是8,是因为直达v1的顶点只有v0和v4,v0->v1的成本要比v0->v4->v1高,所以v0->v4->v1是最优解)
如下图:

如上图,还需要继续检查v1指向的顶点即v2、v4,最后只会修改对应的final值为false即目前还没有确定最短路径的顶点的dist和path信息,因此需要修改v2顶点对应的dist和path信息,
此时就需要检查到达v2,如果经过v1的话,那么有没有可能在之前找到的路径外存在更短的路径呢?
对于v2,之前找到的从v0到达v2的最短路径长度为13,路径信息是v0->v4->v3->v2,该路径最终是从v3直达v2的,但是现在如果从v1直达v2,可以找到一条总长度为5加3加1即9的路径,路径信息为v0->v4->v1->v2,该路径要比v0->v4->v3->v2的成本更低,所以要把v2对应的dist值修改为9,同时把v2对应的path值修改为1即前驱是v1(v1在path数组中的索引为1);
如下图:
如下图,开始第四轮的处理:

如上图,循环遍历三个数组final、dist、path全部的信息,从中找到还没确定最短路径的顶点即对应的final值为false、dist值最小的顶点,
显然在final值为false、dist值最小的顶点中找到的是v2顶点,开始处理v2顶点,
此时把v2顶点对应的final值设为true,表示现在已经可以确定对于v2顶点来说,从起点v0到v2的最短路径长度就是9,并且它的直接前驱是1索引上的顶点即v1,因此就确定了v0到v2的最短路径,
如下图:

如上图,还需要继续检查v2指向的顶点即v3,最后只会修改对应的final值为false即目前还没有确定最短路径的顶点的dist和path信息,由于v3对应的final值为true,因此v3不会作任何处理,
至此v2处理完毕,如下图:

如上图,所有顶点对应的final值都为true即所有顶点都被处理完毕,
至此,Dijkstra算法结束。
3.对于本例如何使用数组信息?

对于最终得出的三个数组final、dist、path,
比如此时要找到起点v0到v2的最短路径的信息,
通过dist数组可知v0到v2的最短路径的总长度为9(就是dist[2]),
通过path数组可以得知该最短路径的内容,path数组中v2是从1索引上的顶点即v1过来的,v1是从4索引上的顶点即v4过来的,v4是从0索引上的顶点即v0过来的,此时找到了起点v0,因此可知该最短路径的内容为v0->v4->v1->v2。
4.时间复杂度:

假设图中的顶点的编号从0开始(第一个顶点记作v0,第二个顶点记作v1,以此类推),
现在要找到从v0到达其他顶点的最短路径,
初始化数组final、dist、path,
对于起点v0,
v0的final值设为true,因为一开始就可以确定从起点v0到v0的最短路径长度为0,意味着一开始就可以确定到达v0的最短路径,
v0的dist值为0,因为从起点v0到v0的最短路径长度为0,
v0的path值为-1,表示v0没有前驱顶点,因为v0本身就是起点,
对于其他顶点,
final值都设为false,因为一开始无法确定起点v0到达其他顶点的最短路径,
dist值都设为arcs[0] [k],arcs[0] [k]表示的是从起点v0直达其他顶点的弧的长度,如果不存在弧(即无法直达)那么就设为无穷,
需要把起点v0指向的顶点的path值设为0(因为v0在path数组的0索引上,此时就代表前驱为v0),v0没有指向的顶点的path值设为-1(因为前驱不是v0)。
假设图中有n个顶点,接下来需要进行n-1轮处理,因为每一轮的处理都能够确定一个新顶点的最短路径,所以在刚开始只有n-1个顶点没有确定最短路径的情况下,由于每一轮可以确定一个,所以需要n-1轮处理,
在每一轮的处理当中都需要循环遍历所有的顶点找到一个final值为false、dist值最小的顶点,也就是说每一轮的处理都需要把final、dist数组扫描一遍,这些数组的总长度都为n(和顶点个数一样),也就是从final、dist数组中找出final值为false、dist值最小的顶点需要O(n)的时间复杂度(遍历final数组和dist数组是先后关系,不是同时进行的),
除了找到final值为false、dist值最小的顶点之外,还需要检查这一轮中选中的顶点它所指向的顶点,
如果图采用邻接矩阵存储,要找到某一个顶点指向的所有顶点,就需要扫描和这个顶点相关的那一整行(这是有向图,邻接矩阵不对称,就不能扫描列了),扫描邻接矩阵的一整行需要O(n)的时间复杂度即每一轮循环要遍历2n个顶点,所以每一轮的处理总共需要O(2n)的时间复杂度,等价于O(n),
如果图采用邻接表存储,那么找到某一个顶点指向的所有顶点就不需要O(n)的时间复杂度了,因为邻接表中某一个顶点对应的链表已经把该顶点指向的所有顶点的信息都列出来了,不需要遍历所有顶点来找指向的顶点了,但由于从final、dist数组中找出final值为false、dist值最小的顶点无论怎样都需要扫描一遍数组,所以总的时间复杂度为O(n),
由于需要n-1轮处理,所以整个算法的时间复杂度就是O( n * (n-1) ),等于O( n * n - n ),等价于O( n * n ),
若图中有V个顶点,总的时间复杂度就是O( |V| * |V| )。
四.Dijkstra算法 V.S. Prim算法的实现思想:
Dijkstra算法,如下图:

Prim算法,如下图:

对于Prim算法,lowCost数组记录的是图中顶点加入到目前组建的生成树里的最小代价,
而Dijkstra算法,dist数组记录的是当前顶点到达某一个指定顶点的最短路径的值,
但实际上Dijkstra算法里的dist数组和Prim算法里的lowCost数组作用类似,
假设图中有V个顶点,由于Prim算法和Dijkstra算法的执行过程类似,所以Prim算法和Dijkstra算法的时间复杂度也是相同的,都是O( |V| * |V| )。
五.Dijkstra算法不适用于负权值带权图:
如果带权图里存在权值为负数的边,那么Dijkstra算法就有可能会失效,找不到最短的带权路径,
如下图的例子,假设找出从顶点v0到达其他顶点的最短路径,
需要初始化三个数组final、dist、path(这3个数组中数据的内容都依次对应v0顶点、v1顶点、v2顶点)->
1.final数组表示目前为止是否找到从起点v0出发到达其他顶点的最短路径:
对于v0顶点,v0顶点对应的final值初始化为true,因为起点是v0,从起点v0到v0的最短路径就是0,意味着一开始就可以确定到达v0的最短路径,
对于v1、v2顶点,v1、v2对应的final值都初始化为false,因为一开始都无法确定从起点v0出发到达这些顶点的最短路径;
2.dist数组表示目前为止能够找到的最短路径的总长度:
对于v0顶点,起点v0到v0的最短路径长度为0,因此v0对应的dist数组的值为0,
对于v1顶点,一开始能找到一条v0直达v1的边,所以目前来看v0到v1的最短路径是10,因此v1对应的dist数组的值为10,
对于v2顶点,一开始能找到一条v0直达v2的边,所以目前来看v0到v2的最短路径是7,因此v2对应的dist数组的值为7,
3.path数组用于记录每一个顶点在最短路径上的直接前驱:
对于v0顶点,v0顶点对于起点v0而言不存在最短路径,也就不存在直接前驱,所以v0对应的path值为-1,
对于v1顶点,目前能够确定的从起点v0到达v1的最短路径就是从v0直达v1,因此v1对应的path值初始化为0(0就是v0在path数组里的索引),
对于v2顶点,目前能够确定的从起点v0到达v2的最短路径就是从v0直达v2,因此v2对应的path值初始化为0,
如下图:

如上图,开始第一轮的处理:
循环遍历三个数组final、dist、path全部的信息,从中找到还没确定最短路径的顶点即对应的final值为false、dist值最小的顶点,
显然在final值为false、dist值最小的顶点中找到的是v2顶点,开始处理v2顶点,
此时把v2顶点对应的final值设为true,表示现在已经可以确定对于v2顶点来说,从起点v0到v2的最短路径长度就是7,并且它的直接前驱是0索引上的顶点即v0,因此就确定了v0到v2的最短路径,
如下图:

如上图,开始第二轮的处理:
循环遍历三个数组final、dist、path全部的信息,从中找到还没确定最短路径的顶点即对应的final值为false、dist值最小的顶点,
显然在final值为false、dist值最小的顶点中找到的是v1顶点,开始处理v1顶点,
此时把v1顶点对应的final值设为true,表示现在已经可以确定对于v1顶点来说,从起点v0到v1的最短路径长度就是10,并且它的直接前驱是0索引上的顶点即v0,因此就确定了v0到v1的最短路径,
如下图:

如上图,所有顶点对应的final值都为true即所有顶点都被处理完毕,
至此,Dijkstra算法结束。
但事实上,如果是从v0->v1->v2这条路径到达v2,由于v1与v2之间的边的权值是负数,所以该条带权路径长度总和为10加-5即5,显然比Dijkstra算法找到的最短路径长度为7的路径v0->v2成本更低,
因此对于v2,使用Dijkstra算法找到的最短路径并不是最优的,
所以Dijkstra算法不适合有负权值边的带权图。
(图什么时候会用到带负权值的边呢?
例一:比如吃鸡游戏,会有一个毒圈,比如此时站在毒圈内,就会一直掉血,以上图为例,假设站在毒圈内v0的位置,现在可以选择直接跑到毒圈外v2的位置,整个跑毒的过程会掉7点血,第二个方案是毒圈内v1这个地方有一个血包,可以先到v1处捡到血包,再跑出毒圈,到达v1会掉10滴血,再捡血包,跑出毒圈之后通过血包可以恢复5点血,总体来看用第二个方案来跑毒的话掉血的代价更小,所以这种场景下就会用到带负权值的边的图。
例二:以上图为例,此时有v0、v1、v2三个地方,可以选择从v0直接开车到v2,开的是电动车,要消耗7格电,还有一种方案可以先从v0开到v1,需要消耗10格电,但是从v1到v2这一段路由于都是下坡,因此可以不费电的让车滑下去,车在往下滑的过程中又可以利用轮子的转动来自己发电,那整个下滑的过程中又可以恢复5格电,所以用第二种方案来走到v2,总的耗电量更低)。
相关文章:

6.10.单源最短路径问题-Dijkstra算法
一.BFS算法的局限性: 如上图,BFS算法可以解决无权图的单源最短路径问题, 如果是解决带权图的单源最短路径问题,BFS算法就不适用了,如下图: 如上图,比如求G港到其他顶点的最短路径, …...
)
Python基于深度学习的网络舆情分析系统(附源码,部署)
大家好,我是Python徐师兄,一个有着7年大厂经验的程序员,也是一名热衷于分享干货的技术爱好者。平时我在 CSDN、掘金、华为云、阿里云和 InfoQ 等平台分享我的心得体会。 🍅文末获取源码联系🍅 2025年最全的计算机软件毕…...

mysql--索引
索引作为一种数据结构,其用途是用于提升检索数据的效率。 分类 普通索引(INDEX):索引列值可重复 唯一索引(UNIQUE):索引列值必须唯一,可以为NULL 主键索引(PRIMARY KEY&a…...

【算法题】荷兰国旗问题[力扣75题颜色分类] - JAVA
一、题目 二、文字解释 1.1 前言 本题是经典的「荷兰国旗问题」,由计算机科学家 Edsger W. Dijkstra 首先提出。如同图中所示的荷兰国旗,其由红、白、蓝三色水平排列组成。在算法领域,该问题可类比为将一个由特定的三种元素(可…...

【数据结构】堆的完整实现
堆的完整实现 堆的完整实现GitHub地址前言堆的核心功能实现重温堆的定义堆结构定义1. 堆初始化与销毁2. 元素交换函数3. 堆化操作向上调整(子→父)向下调整(父→子) 4. 堆元素插入5. 堆元素删除6. 辅助功能函数堆的判空获取堆顶元…...
)
软考 系统架构设计师系列知识点之杂项集萃(51)
接前一篇文章:软考 系统架构设计师系列知识点之杂项集萃(50) 第80题 设三个煤场A1、A2、A3分别能供应煤7、12、11万吨,三个工厂B1、B2、B3分别需要10、10、10万吨,从各煤场到各工厂运煤的单价(百元/吨&…...

patch命令在代码管理中的应用
patch 是一个用于将差异文件(补丁)应用到源代码的工具,常用于修复 bug、添加功能或调整代码结构。在您提供的代码中,patch 命令通过一系列补丁文件(.patch)修改了 open-amp 库的源代码。 patch 命令的核心作…...

Qt结构体运算符重载指南
在 Qt 中,结构体(struct)或类(class)中重载运算符是一种常见的做法,用于实现自定义类型的逻辑操作(如比较、算术运算等)。以下是一些常见的运算符重载示例和注意事项: 1.…...

基于bert预训练模型的垃圾短信分类系统
文章目录 任务介绍数据说明注意事项数据处理数据准备数据集划分数据集类构建模型构建与训练模型构建模型训练模型推理附录任务介绍 随着移动通信技术的飞速发展,短信(Short Message Service, SMS)已成为人们日常生活中不可或缺的沟通方式之一。然而,垃圾短信(Spam SMS)的…...
)
[Android] 网易爆米花TV 2.0.0.0429(原网易Filmly,支持多网盘的TV版、电脑版带海报墙播放器)
[Android] 网易爆米花 链接:https://pan.xunlei.com/s/VOPDuQS9D7qixvAnoy7-he2PA1?pwdhzvh# [Android] 网易爆米花TV 2.0.0.0429(原网易Filmly,支持多网盘的TV版、电脑版带海报墙播放器) 详细介绍直接上主页截图,…...

# 前后端分离象棋对战项目开发记录
1. **结构清晰**:使用更直观的标题、分段和列表,增强可读性。 2. **视觉美观**:添加Markdown格式化(如代码块、加粗、斜体),并建议配色和排版风格。 3. **内容精炼**:精简冗余表述,突…...

Android Framework学习二:Activity创建及View绘制流程
文章目录 Window绘制流程Window Manager Service(WMS)SurfaceSurfaceFlinger 安卓View层次结构ActivityPhoneWindowActivity与PhoneWindow两者之间的关系ViewRootImplDecorViewDecorView 的作用DecorView 的结构总结 Activity创建流程View invalidate调用…...
与图像处理》)
文章五《卷积神经网络(CNN)与图像处理》
文章5:卷积神经网络(CNN)与图像处理——让AI学会"看图说话" 引言:你的AI宠物如何认出猫狗? 想象你的手机突然有了"眼睛",不仅能识别照片里的猫狗,还能告诉你它们的品种&am…...

Ubuntu系统下Firefox浏览器完整指南:故障修复、国内版安装与下载加速
Ubuntu系统下Firefox浏览器完整指南:故障修复、国内版安装与下载加速 一、Firefox无法启动问题修复二、替换国际版安装国内版完整流程准备工作操作步骤验证要点 三、下载延迟问题解决方案现象分析优化配置步骤注意事项 四、进阶技巧补充五、常见问题FAQ 一、Firefox…...

【论文阅读一】掌握高效阅读法,开启学术研究新旅程:S. Keshav教授论文阅读的三遍法
文章目录 一、三遍阅读法1. 初读:10分钟:宏观把握,快速筛选2. 第二遍:1个小时:更仔细的阅读,了解文中论点3. 第三遍:深入理解,注重细节,挑战假设 二、运用三遍阅读法进行…...

多线程编程的常见问题
目录 1. 线程安全和可重入函数问题 2. 死锁的理解 2.1 死锁的概念 2.2 死锁的四个必要条件 3. C中STL容器的线程安全问题 4. C中智能指针的线程安全问题 1. 线程安全和可重入函数问题 线程安全:线程安全是指在多线程环境下,一个函数或者一段代码可…...
【滑动窗口】)
算法篇(九)【滑动窗口】
如果在分析一道算法题的时候,发现使用的两个 ”双指针“ , 都是同向的 , 不回退的 , 且一直都在维护 “一段连续的区间” , 此时我们可以考虑使用 “滑动窗口” ! 一、长度最小的子数组 209. 长度最小的子…...

【AI面试准备】传统测试工程师Prompt Engineering转型指南
介绍技能转型:传统测试工程师需掌握Prompt Engineering优化AI输出。如何快速掌握,以及在实际工作中如何运用。 传统测试工程师向AI时代的技能转型,掌握Prompt Engineering(提示工程)已成为提升工作效率、适应智能化测…...
(文末有下载方式))
数字智慧方案6186丨智慧应急指挥解决方案(43页PPT)(文末有下载方式)
资料解读:智慧应急指挥解决方案 详细资料请看本解读文章的最后内容。 在当今社会,各类突发事件频发,应急管理工作面临着巨大挑战。智慧应急指挥解决方案应运而生,旨在提升应急管理的效率和水平,保障人民生命财产安全。…...

d202552-sql
一、184. 部门工资最高的员工 - 力扣(LeetCode) 要找到每个部门工资最高的 使用窗口函数 加排序函数 排序函数用rank dense_rank都行 把最高相同的找出来就行 select *, dense_rank() over(partition by departmentId order by Salary desc) as rank …...

cpper 转 java
快速上手 java 特性 文章目录 java 语言特点JVM工作过程组成 java 语言特点 Java 程序编译成字节码,然后由 Java 虚拟机(JVM)执行 不同平台适配相同的 JVM ,从而使得 Java 程序具备跨平台性 —— 一次编写,到处运行 …...

PostgreSQL常用函数
常用函数 数值函数 名称作用AVG(col)列的平均值COUNT(col)列的行数MAX(col)列的最大值MIN(col)列的最小值SUM(col)列值求和 字符串函数 名称作用LENGTH(str)计算字符串长度CONCAT(str1,str2)合并字符串LTRIM(col,str)从字串string的开头删除只包含str(默认空白LTRIM(col))R…...

P2196 [NOIP 1996 提高组] 挖地雷
P2196 [NOIP 1996 提高组] 挖地雷 - 洛谷 题目描述 在一个地图上有N(N ≤ 20)个地窖,每个地窖中埋有一定数量的地雷。同时,给出地窖之间的连接路径。当地窖及其连接的数据给出之后,某人可以从任一处开始挖地雷&#…...

截图软件、画图软件、左右分屏快捷键
截图软件 画图软件 画图时候按字母可以改变颜色:红色r,蓝色b,绿色g,粉色p,橙色o 左右分屏:...

小刚说C语言刷题—1018三角形类别
1.题目描述 输入三个整数,以这三个数为边长,判断是否构成三角形;若不能输出 no 。 若构成三角形,进一步判断它们构的是:锐角三角形或直角三角形或钝角三角形。 分别输出 ruijiao , zhijiao , dunjiao 。 输入 三个…...

【Linux】PetaLinux开发
使用Xilinx的PetaLinux工具编译用于Zynq7020的Linux. 部分图片和经验来源于网络,若有侵权麻烦联系我删除,主要是做笔记的时候忘记写来源了,做完笔记很久才写博客。 专栏目录:记录自己的嵌入式学习之路-CSDN博客 目录 1 一般开发流程 2 离线编译过程 3 系统根文…...

【计算机网络网络层深度解析】从IP协议到路由优化
目录 前言技术背景与价值当前技术痛点解决方案概述目标读者说明 一、技术原理剖析核心概念图解核心作用讲解关键技术模块说明技术选型对比 二、实战演示环境配置要求核心实验实现实验1:IPv6地址配置实验2:OSPF路由配置实验3:NAT转换验证 运行…...

第 12 届蓝桥杯 C++ 青少组中 / 高级组省赛 2021 年真题
一、选择题 第 1 题 题目:下列符号中哪个在 C++ 中表示行注释 ( )。 A. ! B. # C. ] D. // 正确答案:D 答案解析: 在 C++ 中,//用于单行注释(行注释),从//开始到行末的内容会被编译器忽略。选项 A(!)、B(#)、C(])均无注释功能,其中#常用于预处理指令(如#inclu…...

【quantity】5 derive_more库 2.0 版介绍
derive_more 是一个 Rust 过程宏库,旨在通过派生宏自动生成常见 trait 的实现,减少样板代码。2.0 版本带来了多项改进和新特性。 主要特性 1. 支持的 Trait 派生 derive_more 2.0 支持派生以下 trait: 基本操作 trait: Display - 格式化显…...

Qt编译报错:Unexpected compiler version, expected Clang 18.0.0 or newer——Qt安装MSVC编译器
截止到本人所使用的Qt6.6.3为止,Qt尚不支持MSVC2022编译器的默认编译器配制。所以,在Qt构建套件中使用MSVC编译器的话,可能仍需要调整Visual Studio版本,或者手动设置MSVC编译器。 如果你的系统安装的是Visual Studio2022&#x…...
角色与动画的性能优化 | UnrealFest演讲干货)
(转)角色与动画的性能优化 | UnrealFest演讲干货
八、蓝图 8.1. Tick 优化的重点关注对象——Tick事件。在不需要的情况下,请默认关闭Tick。 在蓝图中Actor上关掉还不行,Component也需要关掉。 在CPP中,我们可以从PrimaryActorTick或PrimaryComponentTick中关闭Tick。 如果需要Tick&…...

小程序云开发-环境配置
如果点 云开发 没有反应,需要修改软件安装目录不要有中文,但软件名可以是中文: 首次使用,会送1个月的云开发,配置后要等10分钟以后,才可以使用 如果不能选择环境,关掉重新打开一次。 然后记…...

【c++】【STL】priority_queue详解
目录 priority_queue的作用priority_queue的接口构造函数emptysizetoppushpopswap priority_queue的实现仿函数(函数对象)是什么?向上调整算法(adjustup)向下调整算法(adjustdown)迭代器构造pus…...

C语音中的三元运算符
一、三元运算符的基本语法 三元运算符,也被称为条件运算符,是 C 语言中唯一有三个操作数的运算符。它的语法格式为:condition ? expression1 : expression2。从语法结构可以看出,三元运算符由一个条件表达式和两个普通表达式组…...

C++模板知识
目录 引言 一、非类型模板参数 二、类模板的特化 (一)概念 (二)函数模板特化 (三)类模板特化 1. 全特化 2. 偏特化 (四)类模板特化应用示例 三、模板的分离编译 …...

MCP 探索:微软 Microsoft MarkItDown MCP ,可把 Word、Excel 等转换成 MarkDown 格式
简简单单 Online zuozuo: 简简单单 Online zuozuo 简简单单 Online zuozuo 简简单单 Online zuozuo 简简单单 Online zuozuo :本心、输入输出、结果 简简单单 Online zuozuo : 文章目录 MCP 探索:微软 Microsoft MarkItDown MCP ,可把 Word、Excel 等转换成 MarkDown 格式…...

文本中地理位置提取方法—正则和NLP模型
这里写目录标题 一、提取地址列后12个字二、正则表达式删除不需要的文本三、保留关键字并删除之后的字四、相似度计算,查重五、去重 大量的文本中识别数据,要充分考虑效率和准确率。本文的方案是通过正则和NLP门址模型联合识别的方案。 首先利用现有粗略…...

AI大模型-RAG到底能做些什么?
RAG常见的应用场景,有以下几个方面: 1.智能客服系统:比如电商领域,对客户提出的常见问题,进行自动回复。减少人力成本。 2.人力资源管理:一个新的员工,入职一家大型公司,公司中有各…...

【算法基础】冒泡排序算法 - JAVA
一、算法基础 1.1 什么是冒泡排序 冒泡排序是一种简单直观的比较排序算法。它重复地走访待排序的数列,依次比较相邻两个元素,如果顺序错误就交换它们,直到没有元素需要交换为止。 1.2 基本思想 比较相邻元素:从头开始…...

Nginx搭建test服务器
创建test域名 进入阿里云添加解析 创建域名:test.xxxxx.com 服务器复制项目代码 新建目录,Git拉取项目代码,安装上插件包 修改配置文件,启动测试服务 修改配置文件“服务器接口” 开启服务pm2 start app.js --name "t…...

依赖倒置原则
当然可以!这次我们来详细讲解 依赖倒置原则(DIP: Dependency Inversion Principle),它是 SOLID 五大设计原则中的压轴,也是最关键的“架构型原则”。 我将从: 什么是依赖倒置原则(定义&#x…...

PostgreSQL 的 VACUUM 与 VACUUM FULL 详解
PostgreSQL 的 VACUUM 与 VACUUM FULL 详解 一、基本概念对比 特性VACUUMVACUUM FULL定义常规维护操作,清理死元组激进重组操作,完全重写表数据锁级别不阻塞读写(共享锁)排他锁(阻塞所有操作)空间回收只标记空间为可用,不返还OS空间返还操作…...

SQL面试题——留存分析之使用bitmap 计算留存
使用bitmap 计算留存 之前我们说过,留存分析其实在企业数据分析中,是很基础但是也很重要的,留存分析可以反映产品的发展是否健康,是否可持续发展,之前我们介绍过,可以看看之前的文章 SQL面试题——留存分析 因为使用工具的限制,所以我们实现方式也会有所不同,之前我们…...

P2415集合求和 题解
P2415 集合求和 题解 公式推导: 设集合有 n 个元素,记为 a 1 , a 2 , … , a n a_1, a_2, \dots, a_n a1,a2,…,an。 每个子集要么包含某个元素,要么不包含。 我们固定某个元素 a k a_k ak,再从剩下的 n − 1 n -…...

【2025年五一数学建模竞赛】C题 完整论文 模型建立与求解
目录 2025年五一数学建模竞赛 C题完整论文:建模与求解 Matlab代码一、问题重述二、模型假设与符号说明2.1 模型基本假设2.2 符号说明 问题一:预测博主新增关注数问题二:预测用户的新关注行为问题三:预测用户在线状态及互动博主问题…...

wpf 输入框 在输入时去除水印
wpf ScrollViewer 在输入数据时去除水印 在WPF(Windows Presentation Foundation)中,ScrollViewer控件通常用于显示滚动内容。如果你想在ScrollViewer中使用数据输入(例如文本输入),并且希望在输入时去除水…...
(文末有下载方式))
数字智慧方案5857丨智慧机场解决方案与应用(53页PPT)(文末有下载方式)
资料解读:智慧机场解决方案与应用 详细资料请看本解读文章的最后内容。 随着科技的飞速发展,智慧机场的建设已成为现代机场发展的重要方向。智慧机场不仅提升了旅客的出行体验,还极大地提高了机场的运营效率。本文将详细解读沃土数字平台在…...
)
C语言-指针(二)
一级指针 一级指针指的是存储了变量地址的指针 一级指针的变量类型是 类型 * 一级指针的类型与变量的类型有些不同 例:int * p 前面的int * 是该地址的类型 int a 0; int * p a; 这里的指针 p 就是一级指针 二级指针 指针变量也是变量因此也会有地…...

React 组件prop添加类型
给函数的props做注解 import { useState } from reacttype Props { className:string,title?:string } // 自定义一个Button组件 function Button(props:Props){// 解构出classname\const {className} propsreturn <button className{className}>点击我</button&g…...

Spring Boot中集成Guava Cache或者Caffeine
一、在Spring Boot(1.x版本)中集成Guava Cache 注意: Spring Boot 2.x用户:优先使用Caffeine,性能更优且维护活跃。 1. 添加依赖 在pom.xml中添加Guava依赖: <dependency><groupId>com.google.guava</groupId&…...
