数据结构第七章(一)-顺序查找和折半查找
数据结构第七章(一)
- 顺序查找和折半查找
- 一、查找
- 1.平均查找长度(ASL)
- 二、顺序查找
- 1.实现
- 2.算法优化
- 三、折半查找
- 1.实现
- 2.查找判定树
- 四、分块查找
- 1.算法思想
- 2.查找效率分析(ASL)
- 总结
顺序查找和折半查找
一、查找
查找就是对比然后找,可能找得到,也可能找不到
查找——在数据集合中寻找满足某种条件的数据元素的过程称为查找
查找表(查找结构)——用于查找的数据集合称为查找表,它由同一类型的数据元素(或记录)组成
概念都比较复杂,其实查找表就是你在什么东西里面查找,这个东西就是查找表。可能是线性结构,也可能是链式存储啥的。
关键字——数据元素中唯一标识钙元素的某个数据项的值,使用基于关键字的查找,查找结果应该是唯一的。
就是你找的是啥。
注意关键字是唯一标识的哈,比如数据库主键啥的。
对于查找表而言,我们一般进行两种常见操作:
- 查找符合条件的数据元素
- 插入、删除某个数据元素
打比方如果是静态查找表,那我们一般进行的就是第一种,只做查找,所以我们仅关注查找速度即可;如果是动态查找表,除了查找速度,也要关注插入、删除操作是否方便实现。
我们在进行查找的时候,如何评价一个查找算法是好是坏?主要就是看对比的次数多不多,这个对比次数也叫查找长度
查找长度——在查找运算中,
需要对比关键字的次数称为查找长度
1.平均查找长度(ASL)
所谓平均查找长度,就是把所有数据元素都查一遍所需要的查找长度再除以数据元素的个数,也就是字面意思,取个平均值。
平均查找长度(ASL,Average Search Length)——所有查找过程中进行关键字的比较次数的平均值
当然这是在默认查找任何一个元素的概率都相同的情况,如果不同就拿各自分别需要查找的次数乘以各自的概率再相加就好了。
举个栗子,比如下面这个二叉排序树:
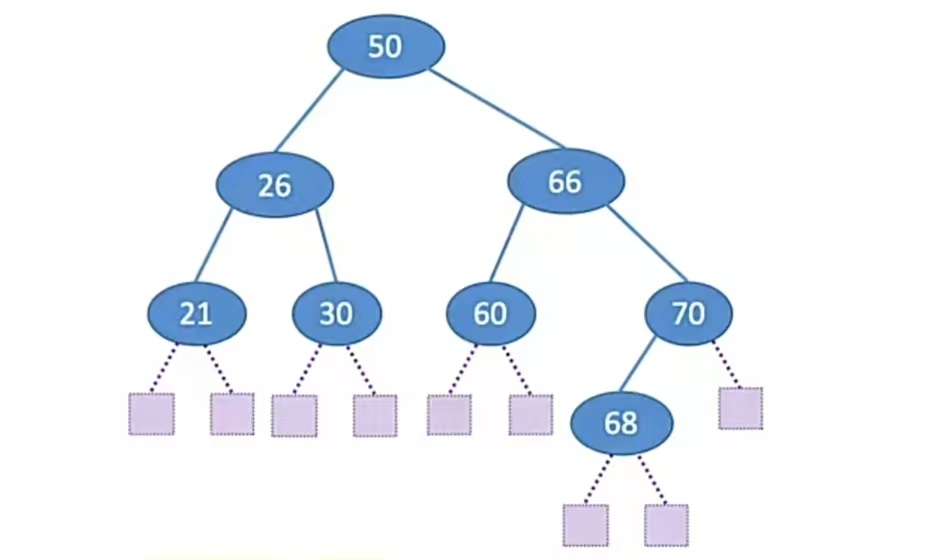
查找成功的平均查找长度ASL:
ASL=(1 * 1 + 2 * 2 +3 * 4 +4 * 1 )/ 8 = 2.625
因为查第一层1个元素的要对比一次,查第二层的2个元素要对比两次,查第三层4个元素的要对比3次,查第四层的1各元素要对比4次,所以总共对比次数就是1 * 1 + 2 * 2 +3 * 4 +4 * 1 ,再求个平均就是查找成功的ASL了。
查找失败的平均查找长度ASL:
ASL=(3 * 7 + 4 * 2 )/ 9 = 3.22
因为查找失败的情况肯定是发现没找到,也就是叶子结点的左右子树的情况,对比3次发现没找到就会落到第三层叶子节点的左右子树上,这一层的情况有7种;对比4次发现没找到第四层叶子结点的左右子树上,这一层的情况有2种,所以所有失败情况总共对比次数就是3 * 7 + 4 * 2,再求个平均就是查找失败的ASL了。
再比如下面这个二叉排序树:
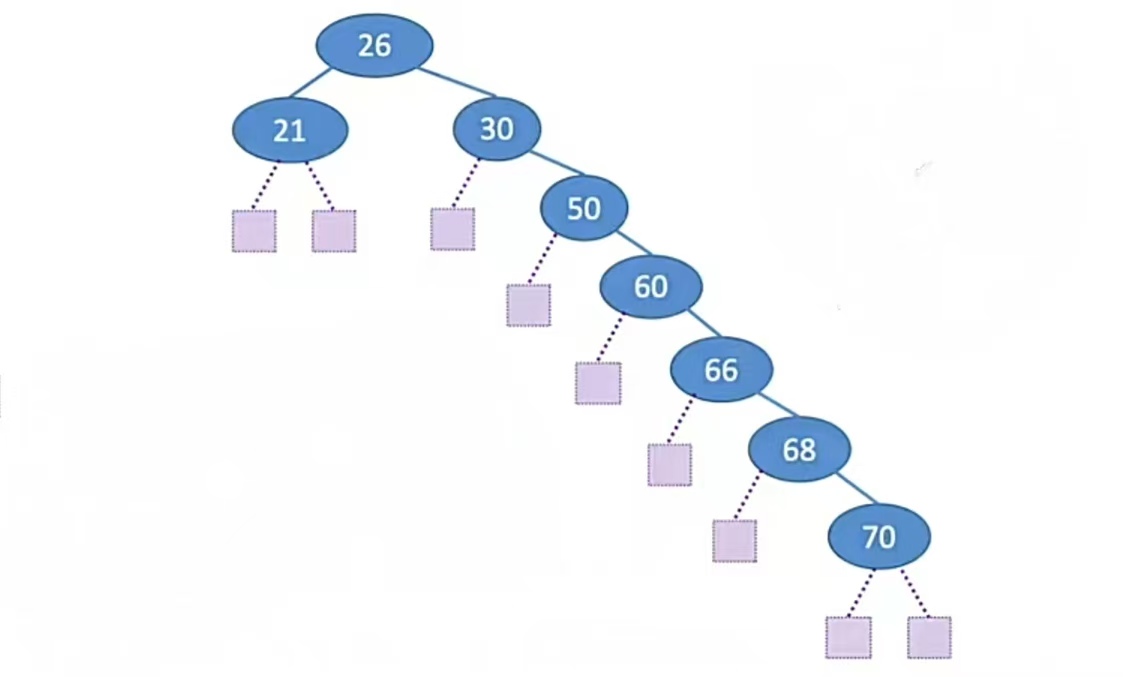
查找成功的平均查找长度ASL:
ASL=(1 * 1 + 2 * 2 +3 * 1 +4 * 1 +5 * 1 +6 * 1 +7 * 1 )/ 8 = 3.75
这个ASL就比上面那个要多,因为它高度比较深嘛,还是高度比较浅的比较好查。
查找失败的平均查找长度ASL:
ASL = (2 * 3 + 3 + 4 + 5 + 6 + 7 * 2 )/ 9 = 4.22
这个失败情况也比上面那个对比次数多。
ASL的数量级反映了查找算法时间复杂度
评价一个查找算法的效率时,通常考虑查找成功/查找失败两种情况的ASL
不止有成功还有失败哈
二、顺序查找
顺序查找就是字面意思,意思是一个一个挨个找就vans了。
顺序查找,又叫“线性查找”,通常用于线性表(也可以用于链表)
算法思想,从前往后挨个找,反过来也是一样的
代码更加直观:
typedef struct{ //查找表的数据结构(顺序表)int *elem; //动态数组基址int tableLen; //表的长度
}SSTable;//顺序查找
int search_seq(SSTable ST, int key){int i;for(i = 0; i<ST.tableLen && ST.elem[i] != key; i++){//查找成功,则返回元素下标;查找失败,则返回-1return i==ST.tableLen ? -1 : i;}
}
比如下面这个顺序表:
| 33 | 10 | 13 | 29 | 16 | 19 | 32 | 7 | 43 | 41 | 37 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | …(下标) |
如果要在其中查找“66”,那么就在这个数组内一个一个比对(这个数组的tableLen是11),发现没有和66相等的,也就是指针i为11,此时查找失败,返回-1;如果要在其中查找“43”,发现当 i 等于 8 时刚好找到,所以返回下标8。
1.实现
我们顺序查找的实现,还可以用另一种方法,也就是下标和第几个数对应。但是要这样的话,0下标的位置就空出来了,所以我们可以在位置0处存放“哨兵”,也就是我们需要找的那个数的值。
也就是说,我们的顺序表就变成这样:
66 | 33 | 10 | 13 | 29 | 16 | 19 | 32 | 7 | 43 | 41 | 37 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | …(下标) |
tableLen还是11
数据从下标1开始存
但是我们这回不是从前往后找了,我们从后往前找,看代码比较清晰:
typedef struct{ //查找表的数据结构(顺序表)int *elem; //动态数组基址int tableLen; //表的长度
}SSTable;//顺序查找
int search_seq(SSTable ST, int key){ST.elem[0] = key; //"哨兵"int i;for(i = ST.tableLen; ST.elem[i] != key; i--){//从后往前找return i; //查找成功,则返回元素下标;查找失败,则返回0}
}
顺序表里没有的话那就从后往前直到遍历到最前面的0下标,哨兵一定是和自己相等的,所以返回0就是没找到;如果找到了那就返回找到的下标,不是0就是找到了。
那么我们这么做和上面的方法有什么区别呢?其实这样更好,因为上面的我们还要看数组是不是越界,越界就是没找到,这个就不用,因为至少也是有个哨兵是等于它自己的。
添加“哨兵”的优点:无需判断是否越界,效率更高
讲完了算法就要分析它的效率,我们先来看查找成功的ASL
显然就是找1次找到,找2次找到……找n次找到,所以ASL成功=(1+2+……n)/ n = (n+1)/2
我们再来看查找失败的ASL
查找失败显然就是遍历完发现没有,然后到哨兵,所以要对比 n+1 次,所以 ASL失败 = n+1
时间复杂度是O(n)
2.算法优化
如果是一个有序表,那我们在表中没有我们要找元素的情况下,就不用再傻乎乎地全部对比完才知道了。比如表中按照从小到大排序,那么我们对比着没找到但发现下一个比它大,就说明后面的也一定找不到了,也就是查找失败了。
打比方我们要在下面这个有序表(查找表中的元素有序存放<递增/递减>):
| 7 | 13 | 19 | 29 | 37 | 43 |
|---|
我们要在这个表中查找 “21”,当我们从前往后对比到“29”的时候,发现 29>21,就说明查找失败了。
我们可以用一个查找判定树来分析它的ASL,如下图所示:
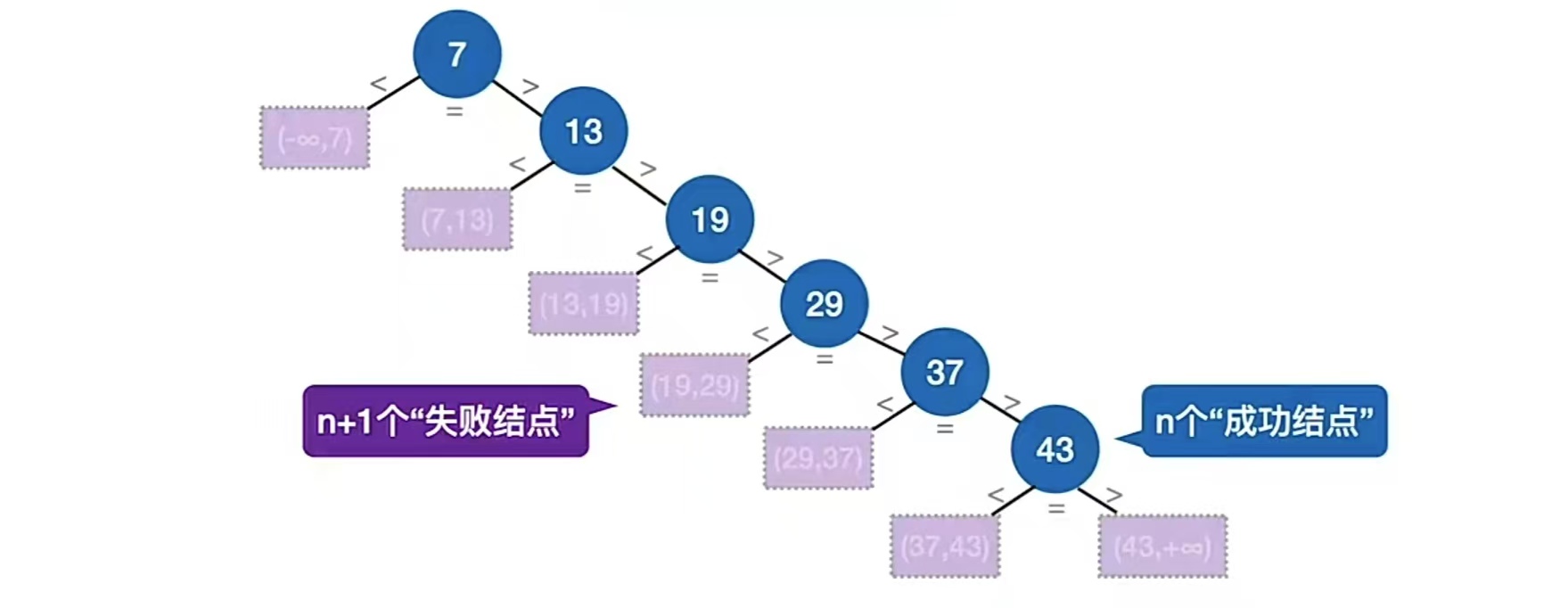
要想知道查找失败时候的ASL,那就得看上面这个图的长方形的叶子结点,每一个叶子结点对应的都是一种查找失败的情况,比7小啦,比13小啦,比43小啦,比43大啦什么的,所以总共有 n+1 种查找失败的情况(n个结点有n+1个空叶子结点,还记得为什么吗?因为我们在线索二叉树里讲过,每一个结点都有左右两个孩子结点,有2n个孩子结点。所有结点都占一个子结点<除了根节点>,所以只占了n-1个,故剩下的就是没被占的n+1个空叶子结点了。)
第一个叶子结点对比一次,第二个对比两次……最后有两个对比n次的,所以:
ASL失败=(1+2+3+……+n+n)/ (n+1)= n/2 + n/(n+1)
一个成功结点的查找长度 = 自身所在层数
一个失败结点的查找长度 = 其父节点所在层数
默认情况下,各种失败情况或成功情况都等概率发生
一共有n个“成功结点”,n+1个“失败结点”。失败结点查找长度为啥是它父节点所在层数?因为它既然失败那肯定是它的父对比发现要么小了要么大了,所以就对比到它父节点,所以对比次数是它父节点所在层数。
当然还有另一种优化的情况,就是在查找概率不相等的时候,把被查概率大的放在靠前的位置可以让我们的ASL更小。
三、折半查找
1.实现
折半折半,顾名思义,就是先对比中间的,看是大了还是小了,然后再在左边/右边分一半,看大了还是小了,一半一半缩小这样。当然,这是基于有序序列的情况。
折半查找,又称“二分查找”,仅适用于
有序的顺序表。
比如下面这个顺序表:(从小到大)
| 7 | 10 | 13 | 16 | 19 | 29 | 32 | 33 | 37 | 41 | 43 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | …(下标) |
tableLen = 11
那既然是折半,肯定要知道折一半之后的位置在哪。所以我们用一个 low指针 ,一个 high指针 ,还有一个 mid指针 来辅助, 初始状态下
low = 0(第一个元素),high = tableLen-1(最后一个元素),mid = (low+high)/2
其实这样看的话让mid = (low+high)/2,如果是奇数个还好,比如如果只有3个,low为0,high为2,mid直接就为1,但如果是偶数个,那这个中轴线你有没有发现其实就是往左偏的,也就是左边就比右边少一个(因为(low+high)/2也就相当于向下取整,舍掉余数嘛,如果让它向上取整那就是右边少一个了)。
举两个栗子:
①我们要查找“33”
初始状态下 low = 0(第一个元素),high = tableLen-1也就是10,那么我们mid( (low+high)/2=5)就是指向 下标5 在的这个元素,也就是“19”,我们发现要找的“33”比“19”大,所以在mid右半边查找,让 low = mid + 1 (6),mid = (low+high)/2(6+10=16, 16/2=8),再接着对比;
所以现在 low 是 6,mid 是 8,下标为8的元素是“37”,我们发现要找的“33”比“37”小,所以在mid左半边找,让 high = mid - 1 (7),mid = (low+high)/2(6+7=13, 13/2=6),再接着对比;
也就是说,现在 high 是 7,mid 是 6(指向和low一样),下标为6的元素是“32”,我们发现要找的“33”比“32”大,所以在mid右半边查找,让 low = mid + 1 (7),mid = (low+high)/2(7+7=14, 14/2=7),再接着对比;
此时!!!皇天不负苦心人,现在 low 是 7,mid 是 7,下标为7的元素是“33”,我们发现要找的“33”和“33”一样,33 == mid,所以
查找成功!
②我们要查找“12”
初始状态下 low = 0(第一个元素),high = tableLen-1也就是10,那么我们mid( (low+high)/2=5)就是指向 下标5 在的这个元素,也就是“19”,我们发现要找的“12”比“19”小,所以在mid左半边查找,让 high = mid - 1 (4),mid = (low+high)/2(0+4=4, 4/2=2),再接着对比;
所以现在 low 是 0,mid 是 2,下标为2的元素是“13”,我们发现要找的“12”比“13”小,所以在mid左半边找,让 high = mid - 1 (1),mid = (low+high)/2(0+1=1, 1/2=0),再接着对比;
也就是说,现在 high 是 1,mid 是 0(指向和low一样),下标为0的元素是“7”,我们发现要找的“12”比“7”大,所以在mid右半边查找,让 low = mid + 1 (1),mid = (low+high)/2(1+1=2, 2/2=1),再接着对比;
此时,现在 low 是 1,mid 是 1,high 也是 1 ,下标为1的元素是“10”,我们发现要找的“12”比“10”大,所以在mid右半边查找,让 low = mid + 1 (2),mid = (low+high)/2(2+1=3, 3/2=1),此时!!!你有没有发现,low>high,这是不应该的,所以
查找失败,可以确定这个表里没有“12”。
这俩栗子差不多了。
上述过程用代码其实很简单,就几句:
typedef struct{ //查找表的数据结构(顺序表)int *elem; //动态数组基址int tableLen; //表的长度
}SSTable;//折半查找
int binary_search(SSTable L,int key){int low = 0, high = L.tableLen - 1, mid;while(low <= high){mid = (low + high) / 2; //取中间位置if(L.elem[mid] == key){return mid; //查找成功则返回所在位置}else if(L.elem[mid] > key){high = mid - 1; //从前半部分继续查找}else{low = mid + 1; //从后半部分继续查找}}return -1; //查找失败,返回-1
}
还记得我们开头说的,只用于顺序表吗?为啥不用于链表,因为顺序表拥有随机访问的特性,链表没有(链表找中间啥的比较麻烦)。
2.查找判定树
什么是查找判定树?
听起来很高级其实没啥,就是把每次的mid找出来当做根节点。首先mid在中间,mid左边就是左子树元素,mid右边就是右子树元素;mid左边的元素再让左边元素的mid当根节点,再分左右,mid右边的元素再让右边元素的mid当根节点,再分左右……这样就可以构造一棵查找判定树了。
比如上面那个有序表的查找判定树就是这样的:
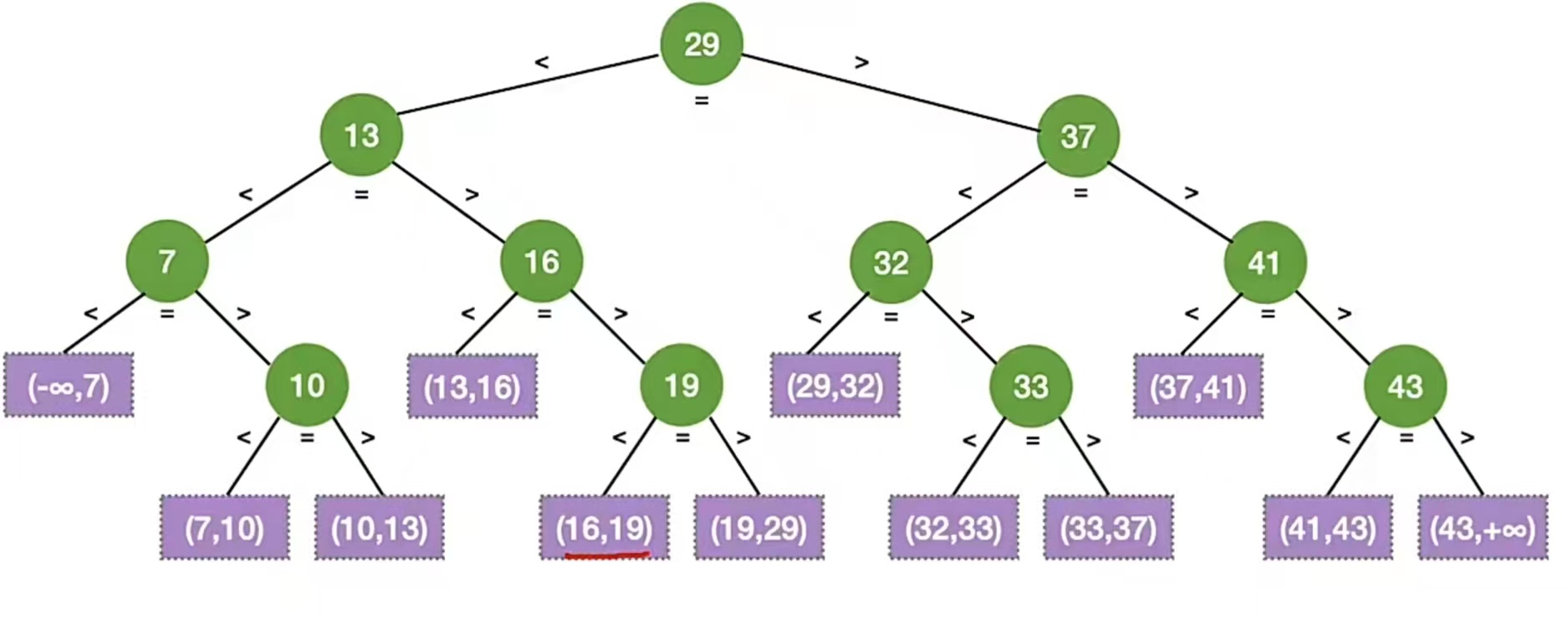
ASL成功=(1 * 1 + 2 * 2 + 3 * 4 + 4 * 4 )/11 = 3
ASL失败=(3 * 4 + 4 * 8 )/12 = 11/3
怎么构造一棵查找判定树?
我们在构造查找判定树的时候:
- 如果当前low和high之间
有奇数个元素,则mid分割后,左右两部分元素个数相同; - 如果当前low和high之间
有偶数个元素,则mid分割后,左半部分比有半部分少一个元素;
所以折半查找的查找判定树中,若 mid = ⌊(low+high)/2⌋,则对于任何一个结点,必有右子树结点数-左子树结点数=0或1
折半查找的判定树一定是
平衡二叉树
因为符合平衡二叉树性质嘛。
那么如果 mid = ⌊(low+high)/2⌋,则含1个元素的查找判定树,含2各元素的查找判定树……含16个元素的查找判定树是什么样的呢(我们不考虑失败结点)?其实按照上面的方法构造就vans了,就是这样:
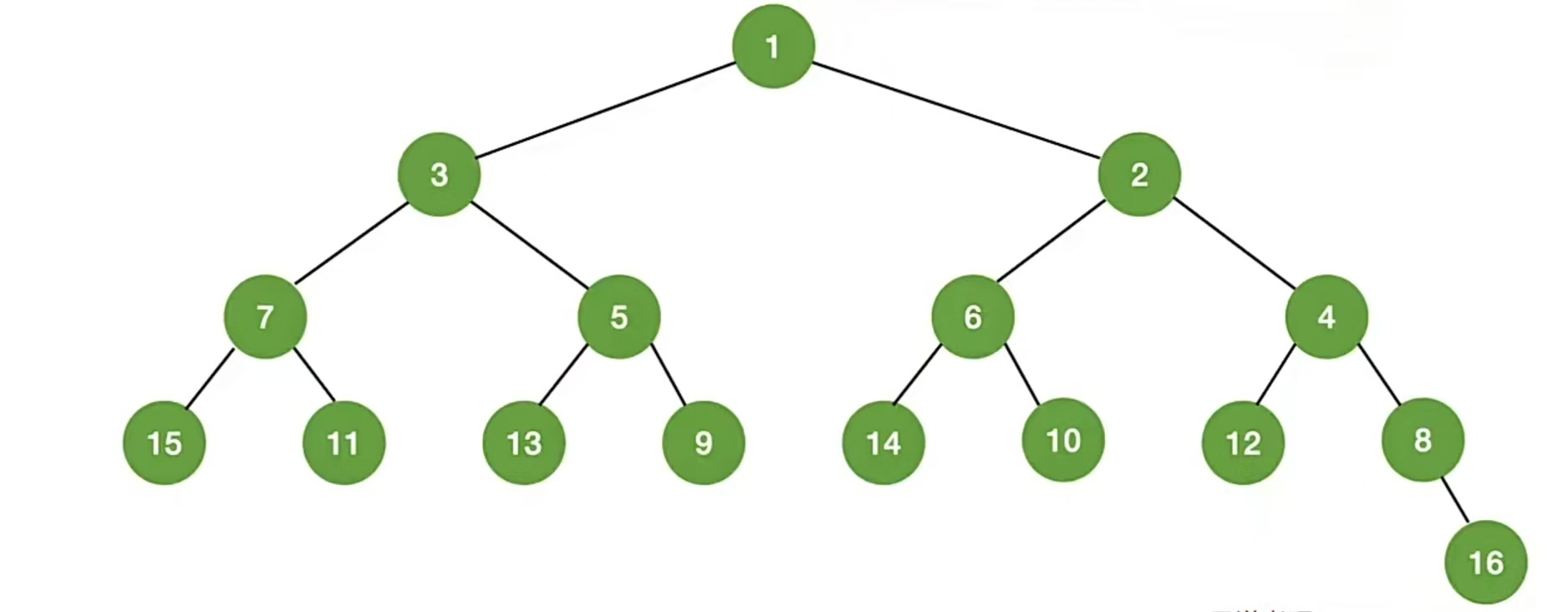
要注意的就是右子树结点数-左子树结点数=0或1,严格遵循这个我们构造的就没毛病了~
折半查找的判定树中,
只有最下面一层是不满的。因此,元素个数为 n 时,树高 h=⌈log2(n+1)⌉(和完全二叉树计算方法一样的)
还记得我们上面的那个查找判定树吗:
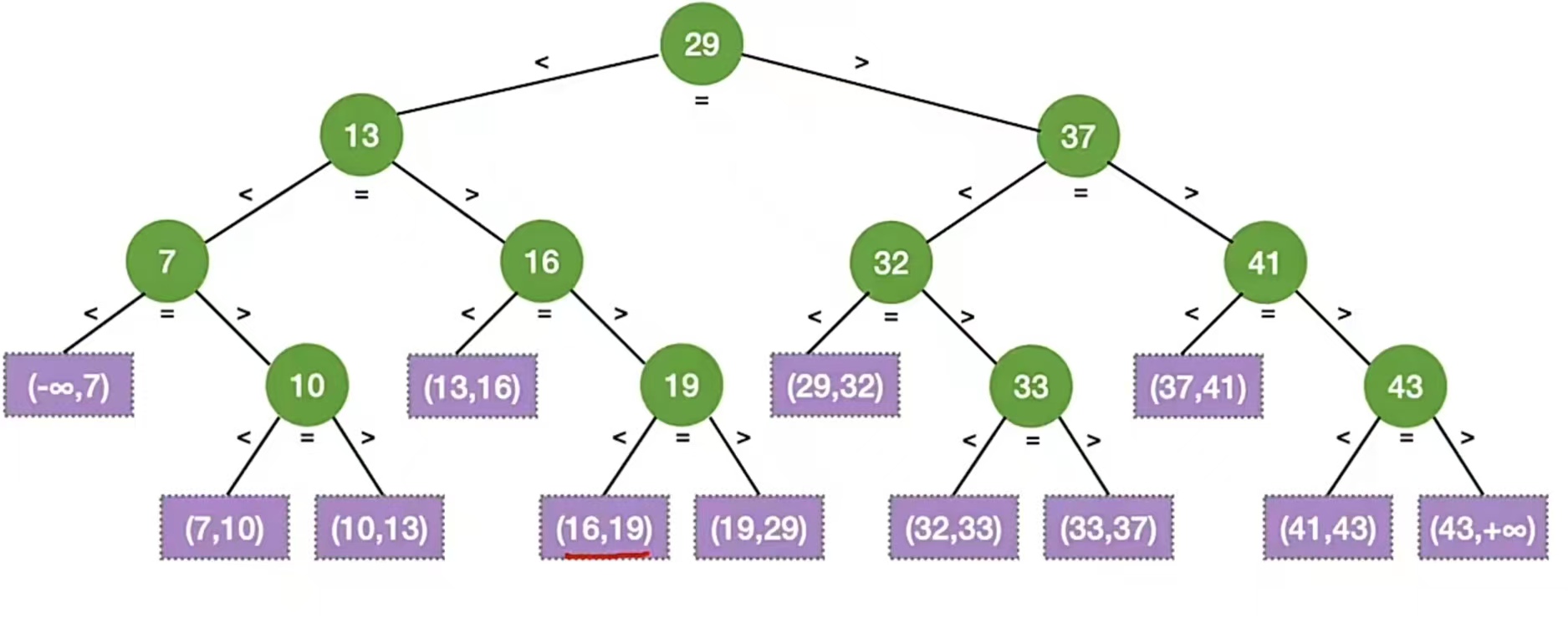
判定树结点关键字:左<中<右,满足二叉排序树的定义;失败结点:n+1 个(等于成功结点的空链域数量)
树高 h = ⌈log2(n+1)⌉(该树高不包含失败结点)
查找成功的ASL≤h,查找失败的ASL≤h
折半查找的时间复杂度为O(log2n)
但是!!!不要以为,折半查找的时间复杂度是O(log2n),顺序查找的时间复杂度为O(n),折半查找的速度就一定比顺序查找更快了,这显然不能说那么死,比如你要找的那个数在第一个,我顺序查找直接第一个对比就对比上了,你折半查找还要从中间一个一个过去,所以这要看情况。
小拓展:如果mid = ⌈(low+high)/2⌉,那么判定树是什么样?其实就左右反过来:
- 如果当前low和high之间
有奇数个元素,则mid分割后,左右两部分元素个数相同; - 如果当前low和high之间
有偶数个元素,则mid分割后,左半部分比有半部分多一个元素;
如果偶数个那就左比右多了;对于任何一个结点,也变成了左子树结点数-右子树结点数=0或1了。
四、分块查找
1.算法思想
分块查找,人如其名,就是分成一块一块的,先找在哪个块,然后再在块内查找。如下图:
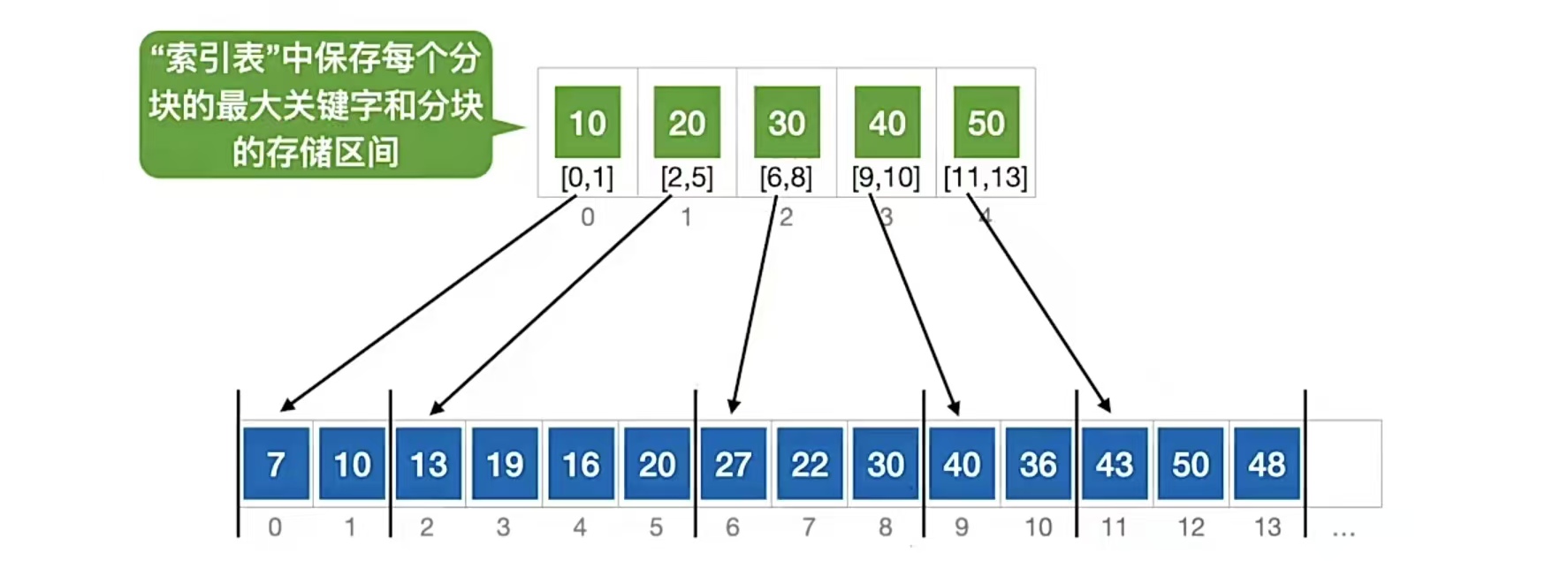
特点:
块内无序,块间有序
找在哪个块的时候可以按照顺序查找,也可以按照折半查找(因为块间有序嘛);找块内元素的时候,只能按照顺序查找(因为块内无序)。
存放每一个块的叫“索引表”,所谓索引表,里面放的就是每一个块的最大关键字;但是我们分块肯定得知道这个快从哪到哪,所以还要存放分块的存储区间,也就是从哪到哪的数组下标。
所以分块查找的结构就显而易见,块,和索引:
//索引表
typedef struct{int maxValue;int low,high;
}Index;//顺序表存储实际元素
int List[100];
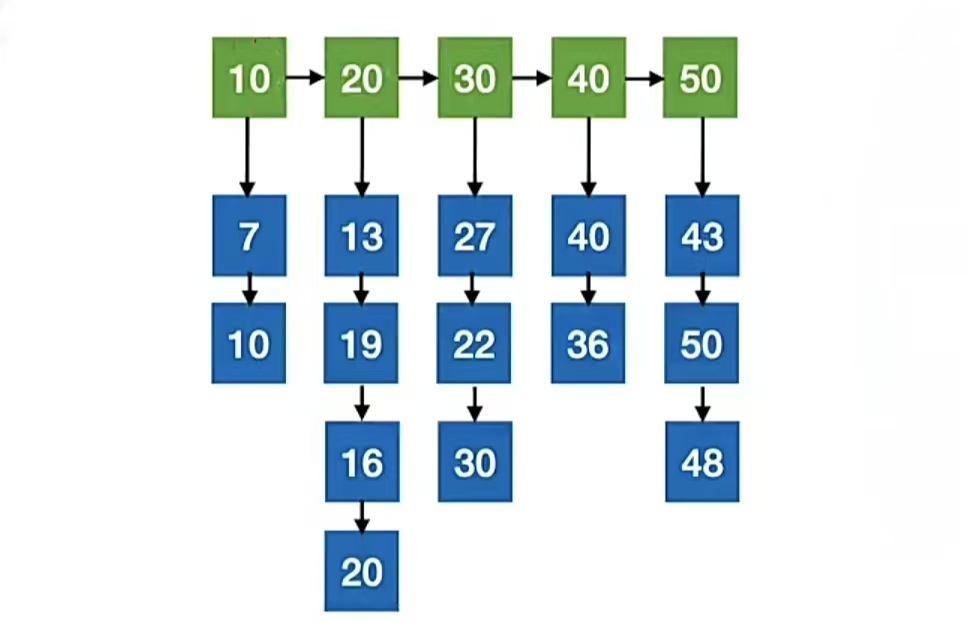
分块查找举个栗子,比如想查找“22”,那么先找块,一个一个找发现“30”比“22”大,所以在“30”指向的这个块中找;“30”指向的块的数组下标是6到8,所以在数组下标为6,7,8里顺序查找,找到“22”了,查找成功。
再比如想查找“29”,还是先找块,一个一个找发现“30”比“22”大,所以在“30”指向的这个块中找;“30”指向的块的数组下标是6到8,所以在数组下标为6,7,8里顺序查找,在这个块中没找到“29”,超出分块范围,查找失败。
分块查找,又称索引顺序查找,算法过程如下:
- 在索引表中确定待查记录所属的分块(可顺序,可折半)
- 在块内顺序查找
比如我们用折半查找来查找索引表,我们要查找“30”这个元素,那么我们low=0,high=4,mid=2,一下就找到了“30”,然后就可以直接去“30”指向的这个块中找;“30”指向的块的数组下标是6到8,所以在数组下标为6,7,8里顺序查找,找到“30”了,查找成功
如果我们要查找“19”,那么初始low=0,high=4,mid=2,发现19<30,high=mid-1=1,mid=(low+high)/2=(0+1)/2=0,和low指向一样,发现19>10,low=mid+1=1,mid=(low+high)/2=(1+1)/2=1,此时low,high,mid全指向一样;19<20,high=mid-1=0,mid=(low+high)/2=(1+0)/2=0,此时low>high
若索引表中不包含目标关键字,则折半查找索引表最终停在low>high,要
在low所指分块中查找
我们在“20”这个块中找;“20”指向的块的数组下标是2到5,所以在数组下标为2,3,4,5里顺序查找,找到“19”了,查找成功
为什么要在low所指分块中查找呢?因为最终low左边一定小于目标关键字,high右边一定大于目标关键字,而分块存储的索引表中保存的是各个分块的最大关键字,所以要在low所指分块中查找。这官方说的看不懂一点是吧,别急
什么意思呢?你看在我们的low>high之前,是不是得有个low=high,这个时候我们的low要大于high了,要么是现在的这个位置的值小于关键字,要么是现在这个位置的值大于关键字是不,如果小于关键字的话,那就得让low=mid+1,所以才会导致low>high,又因为high所指的小于关键字,所以要在low所指的分块中查找;如果大于关键字的话,那就得让high=mid-1,所以才会导致low>high,又因为low所指的本来就大于关键字,分块的块中存放的是那个块最大的,所以要在low所指的分块中查找。(因为我们存放的分块的块是块中最大的,所以就算在索引表中找不到,那我们最终目的一定是找到比关键字大的那个中最小的那个,这个关键字要是有的话一定是在这个里面,当然这都是我自己的理解,仅供参考。)
图在上面有点远了,拉下来方便看:

再举个栗子,如果我们要查找“54”,继续折半查找……(此处过程省略),最后我们会发现,high=4,low=5(越界了),此时我们也不用继续找什么了,因为low超出索引表查找范围,查找失败
这和上面的也一样,上面说最终停在low>high,要在low所指分块中查找,low指向的都越界了,所以一定是找不到了。
2.查找效率分析(ASL)
讲完了算法思想,现在我们开始分析它的查找效率
我们看上面那个图,一共有14个元素,它们各自被查找的概率都为1/14
若索引表采用顺序查找,则7需要对比2次(一次找块的找到“10”对比1次,一次在块内找的找到“7”对比1次)、10需要对比3次(一次找块的找到“10”对比1次,一次在块内找的找到“10”对比2次)……
若索引表采用折半查找,则30需要对比4次(一次找块的找到“30”对比1次,一次在块内找的找到“30”对比3次)、10需要对比3次(一次找块的找到“10”对比2次<第一次是mid=2,和“30”对比,发下10<30,high=mid-1=1,mid=(low+high)/2=(0+1)/2=0,再和“10”对比一次>,一次在块内找的找到“10”对比2次)……
平均查找长度就是顺序表中每个元素的查找需要对比次数相加求平均。
假设,长度为n的查找表被均匀地分为b块,每块s个元素,如下图所示:
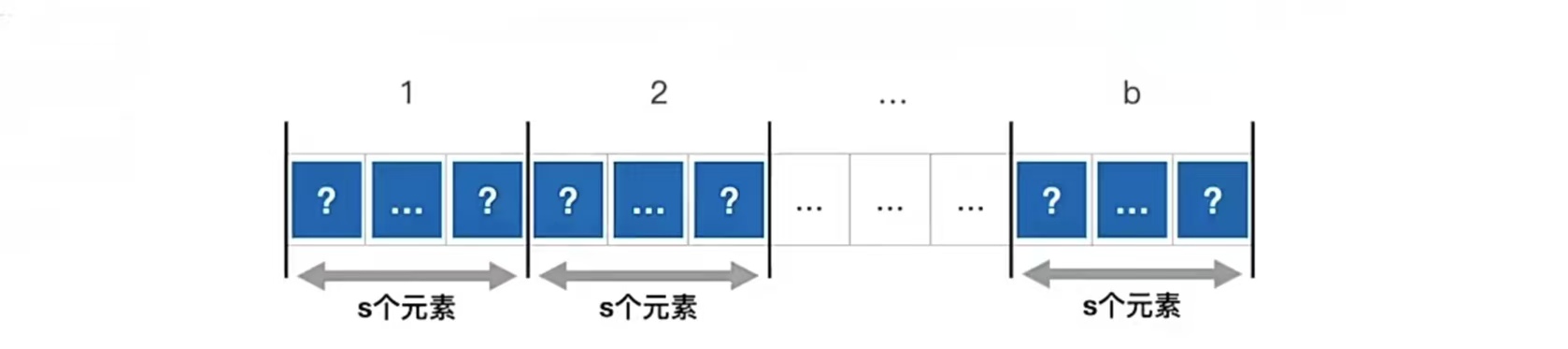
设索引查找和快内查找的平均查找长度分别为 LI, Ls,则分块查找的平均查找长度为ASL = LI + Ls
用顺序查找索引表,则 LI = (1+2+……+b)/ b = (b+1)/2, Ls = (1+2+……+s)/ s = (s+1)/2,则 ASL = (b+1)/2 + (s+1)/2 = (s2 + 2s + n)/2s
当
s=√n时,ASL最小 = √n+1
因为一共有n个元素,被分为b块,每块s个,所以有n=bs,b=n/s,故(b+1)/2 + (s+1)/2 = ( n/s +1)/2 + (s+1)/2 = (s2 + 2s + n)/2s = 1/2 * s + 1 + n/2s ,求导得 ASL` = 1/2 - n/(2s2),当s=√n时导数为0,此时ASL最小 = √n+1。
也就是说,当我们的顺序表被分为 √n 块,每块有√n 个元素时,查找效率最高。比如如果n = 10000,那么应该分100块,每块100个元素,此时ASL最小 = 101,这比顺序查找好很多,顺序查找的话ASL就是5000,效率很低。
用折半查找索引表,则 LI = ⌈log2(b+1)⌉, Ls = (1+2+……+s)/ s = (s+1)/2,则 ASL = ⌈log2(b+1)⌉ + (s+1)/2。
查找失败的情况更加复杂,一般不考。
但是我们的查找表是顺序查找表,所以对于增删操作,就会非常不方便,增删一位后面的就都要移动。所以如果对于增删有很大要求,那么就可以将查找表设为动态查找表,也就是用链式存储(如下图所示):
所以我们得机灵点,随机应变。
总结
顺序查找没什么,折半查找要注意low和high是怎么变化的,不要搞错搞漏了;还有就是要注意分块查找的时候,对索引表进行折半查找时,如果索引表中不包含目标关键字,则折半查找最终停在low>high,要在low所指的分块中查找。
相关文章:
-顺序查找和折半查找)
数据结构第七章(一)-顺序查找和折半查找
数据结构第七章(一) 顺序查找和折半查找一、查找1.平均查找长度(ASL) 二、顺序查找1.实现2.算法优化 三、折半查找1.实现2.查找判定树 四、分块查找1.算法思想2.查找效率分析(ASL) 总结 顺序查找和折半查找…...

springboot项目之websocket的坑:spring整合websocket后进行单元测试后报错的解决方案
前排提醒:还是博主菜,见识短浅,没遇到过这个问题。。。 起因 前段时间学习websocket和sse,写demo用了spring框架。后来又写了新的spring单元测试类demo去测试,结果启动后报错,报错信息提示websocket的相关…...

在单片机编程中充分使用抽象工厂模式,确保对象创建的限制,多使用抽象接口避免多变具体实现类
背景 在软件架构设计上追求稳定,就必须多使用稳定的抽象接口,少依赖多变的实现;具体编码时可以充分使用抽象工厂模式 举例进行详细讲解和说明抽象工厂模式在单片机开发中的应用 抽象工厂模式是一种创建型设计模式,它提供了一种方式,可以将一组相关的对象创建封装到一个…...

喷泉码技术在现代物联网中的应用的总结和参考文献
总结 物联网与 5G 技术高速发展,数据传输对可靠性和实时性提出严苛要求。前向纠错码是增强通信鲁棒性的关键,但平衡冗余资源开销与编解码效率的矛盾是核心难题。LT 码和 Raptor 码是无率码典型。理论上它们能达渐进最优性能,然而实际系统受数据包规模、计算资源等限制,其工…...

vuex与vuex-persistedstate 插件固化数据
一,vuex与vuex-persistedstate 插件固化数据 的小案例 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><title>Vuex基础案例</title></head><body><div id"app"&…...

如何在WordPress网站中设置双重验证,提升安全性
随着互联网的不断进步,网站的安全问题越来越受到重视。尤其对于WordPress这样常用的建站平台,安全性显得尤为重要。尽管WordPress自带一定的安全性,但仅依靠用户名和密码的登录方式仍然存在风险。因此,启用“双重验证”便成为了提…...

2025系统架构师---基于规则的系统架构风格
引言 在业务规则频繁变更、决策逻辑高度动态化的现代企业环境中,基于规则的系统架构风格(Rule-Based System Architecture Style)通过将核心业务逻辑抽象为可配置规则、规则引擎与决策服务的分离,实现了业务敏捷…...

Python排序中lambda函数详解
在 Python 中,lambda 函数是一种匿名函数,通常用于需要一个函数但又不想为其定义一个正式名称的情况。在排序操作中,lambda 函数用于指定排序的依据。 lambda 函数的基本语法 lambda 函数的基本语法如下: lambda arguments: ex…...

web 基础与 http 协议
目录 一 Web 基础 1. 域名和 DNS 1.1 域名的概念 1.2 DNS 2. 网页与HTML 2.1 HTML 概述 2.2 HTML 基本标签 2.3 网站和主页 3. 静态网页与动态网页 3.1 静态网页 3.2 动态网页 二 HTTP 协议 1. HTTP 协议概述 2. HTTP 方法 3. HTTP 状态码 4. HTTP 请求流程分析…...

记一次奇妙的Oracle注入绕WAF之旅
0x01 一个登陆框 上班时遇到了一个登陆框 看着这个复古的界面,于是上手除了admin123456之外顺手点了个 于是弹出了一条有意思的报错 这就有意思了,毕竟已经很久没在登陆框遇到sql注入了,当我想当然的认为万能密码可以秒时,事情出…...

python裁剪小说封面标题
一张矩形图片 比如50*100 大小 中心点的坐标是是(0,0) 左上角是(-25,50) 右上角是(25,50) 左下角是(-25,-50) 右下角是(25,-50) 我希望你能用python,帮我对本地指定图片切割大小,计算出该图片的中心坐标,然后按照我输入的长宽具体值,比…...

高性价比手机如何挑选?
这四个关键点,助你找到心仪机~ 一、性能强者:游戏娱乐畅快到底 处理器相当于手机的 “大脑”,处理速度快、能力强,运行大型游戏毫无压力。 搭配上大容量运存,多任务切换也能秒速完成,再也不怕游戏卡顿啦。…...

Java面试场景深度解析
Java面试场景深度解析 在互联网大厂Java求职者的面试中,经常会被问到关于Java项目中的各种技术场景题。本文通过一个故事场景来展示这些问题的实际解决方案。 第一轮提问 面试官:马架构,欢迎来到我们公司的面试现场。请问您对Java内存模型…...

【DeepSeek认证】最好的MODBUS调试工具
根据搜索结果,MThings 和 Modbus Poll 是当前被广泛推荐且功能强大的MODBUS调试工具。以下是两者的详细对比及推荐理由: 1. MThings 核心优势: 主从一体化:支持同时模拟MODBUS主站和从站,无需切换工具即可完成双向调…...

欧莱雅集团:利用 Google Maps Platform Environment API 提供个性化护肤推荐
在欧莱雅集团,美丽绝不仅仅停留在表面。如今,这一点比以往任何时候都更加真实,因为公司将其深厚的科学专业知识与尖端技术相结合,以重塑美丽的未来。其成功的关键在于承诺不为科技而使用科技。其所有创新都满足了消费者的明确需求…...

2025三掌柜赠书活动第十五期:高并发系统:设计原理与实践
目录 前言 什么是高并发? 高并发系统的挑战 设计原理 1、分布式架构 2、缓存与异步处理 3、数据库优化 4、弹性扩展 实践方法 1、性能监控与分析 2、压力测试 3、故障排查与容错机制 关于《高并发系统:设计原理与实践》 编辑推荐 内容简介…...

【Spark入门】Spark架构解析:组件与运行机制深度剖析
1 Spark架构全景图 Apache Spark作为当今最流行的大数据处理框架之一,其卓越性能的背后是一套精心设计的分布式架构。理解Spark的架构组成和运行机制,对于性能调优和故障排查至关重要。 1.1 核心组件架构 组件交互流程: Driver初始化…...

电子电器架构 -- 汽车零部件DV试验与PV试验的定义及关键差异
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 钝感力的“钝”,不是木讷、迟钝,而是直面困境的韧劲和耐力,是面对外界噪音的通透淡然。 生活中有两种人,一种人格外在意别人的眼光;另一种人无论…...

交换机配置DHCP
交换机配置DHCP 背景先关闭路由器的DHCPconsole口连接到交换机配置交换机 背景 路由器的dhcp分配IP地址变慢,怎么处理 先关闭路由器的DHCP 查看路由器中DHCP地址池范围; 关闭路由器的DHCP console口连接到交换机 协议Serial端口COMX波特率9600流控无 配置交换机…...

【人工智能】边缘智能的突破:Ollama模型压缩技术与DeepSeek部署实践
《Python OpenCV从菜鸟到高手》带你进入图像处理与计算机视觉的大门! 解锁Python编程的无限可能:《奇妙的Python》带你漫游代码世界 随着边缘计算的兴起,将大型语言模型(LLM)部署到资源受限的边缘设备成为研究热点。Ollama凭借其高效的模型压缩技术和轻量级推理框架,为…...

基于STM32、HAL库的DS2401P安全验证及加密芯片驱动程序设计
一、简介: DS2401P是Maxim Integrated(现为Analog Devices)生产的一款1-Wire硅序列号芯片,具有以下特点: 64位唯一ROM编码(包括8位家族码、48位序列号和8位CRC校验码) 单总线接口,…...

日志收集之 logback使用
一 简介 1.1 Logback 是一个用于 Java 应用程序的强大日志框架,广泛应用于企业级应用中。它是由 SLF4J 的创始人开发的,旨在成为 Log4j 的替代品。Logback 提供更高级、更灵活的功能,同时还支持与 SLF4J 的无缝集成。 2.2 Logback分为下面几…...
:Linux下的基本指令)
Linux学习笔记(一):Linux下的基本指令
文章目录 Linux下的基本指令1. ls指令2. pwd指令3. cd指令4. touch指令5. mkdir指令(牢记)6. rmdir指令 && rm 指令(牢记)7. man指令(牢记)8. echo指令9. cp指令(牢记)10. m…...
)
Unity AI-使用Ollama本地大语言模型运行框架运行本地Deepseek等模型实现聊天对话(二)
一、使用介绍 官方网页:Ollama官方网址 中文文档参考:Ollama中文文档 相关教程:Ollama教程 使用版本:Unity 2022.3.53f1c1、Ollama 0.6.2 示例模型:llama3.2 二、运行示例 三、使用步骤 1、创建Canvas面板 具体…...

SDC命令详解:使用get_clocks命令进行查询
相关阅读 SDC命令详解https://blog.csdn.net/weixin_45791458/category_12931432.html?spm1001.2014.3001.5482 get_clocks命令用于创建一个时钟对象集合,关于设计对象和集合的更详细介绍,可以参考下面的博客。需要注意的是,在有些工具中还…...

git 修改用户名和邮箱
在 Git 中修改用户名和邮箱地址是常见的任务,这可以确保你的提交记录使用正确的身份信息。你可以通过简单的命令来完成这一操作。 全局配置 修改全局用户名 要修改全局的用户名,请执行以下命令: git config --global user.name "New…...

pg数据库删除模式
不能直接使用 DROP SCHEMA "app_sys" 删除, 这样会报错 cannot drop schema app sys 20250416 because other objects depend on it DETAlL: extension uuid-ossp depends on schema app sys 20250416sequence app sys 20250416.app sys id seq depend…...

【C++】Googletest应用
Googletest 1 配置 使用cmake配置: 具体文件后面上传补充 ./test.out --gtest_filterXXXTest.xxx 2 gdb 为了跟踪流程,可以使用gdb; gdb ./xxx.out gdb --args ./gtest --gtest_filterxxx.xxx设置运行参数 set args --gtest_filterxxx.…...

QgraphicsView异步线程加载地图瓦片
本节主要记录一下qt开发过程中离线地图瓦片的加载方式,瓦片加载选择graphicsView控件,同时为了不影响主线程事件和其他操作,这里采用了异步线程的操作,将地图瓦片加载的步骤放到了异步子线程之中。注:本记录仅为本人笔…...

机器学习day2
使用KNN算法实现机器学习 给我一个苹果的图片 我能预测出这个是一个苹果 代码: # 导入需要的库 # 读图 import os import cv2 # 绘图 import matplotlib.pyplot as plt import seaborn as sns # 数组 import numpy as np from skimage.feature import hog from sk…...

jquery解决谷歌浏览器自动保存加密密码是乱码
添加一个隐形的input框,提交隐藏input框里的数据,展示框展现的还是明文密码,并且不提交展示框的值 <formid"loginForm"class"form-signin newForm-signin"action"${ctx}/login"method"post"onsub…...
)
Python 如何操作数据库,让你使用 DeepSeek 开发数据库应用更加快 (Orm Bee)
Python 如何操作数据库,让你使用 DeepSeek 开发数据库应用更加快 操作数据库最好用 ORM 工具,可以提高开发效率. ORM 就是实体与数据库表的映射,让我们可以用面向对象的方式来操作数据库. 简单易用,直接上代码. 使用Orm Bee操作…...

如何解决 Linux 文件系统挂载失败的问题
以下是解决Linux文件系统挂载失败问题的系统性排查与解决方案: 一、设备基础检查 确认设备识别状态 执行 lsblk 或 fdisk -l 查看磁盘设备列表,验证目标设备(如 /dev/sdb1)是否被系统识别。 若设备未显示,需排查&a…...

JVM——引入
什么是JVM?它与JDK、JRE的关系? JVM、JRE 和 JDK 是 Java 平台的三个核心组件,各自承担着不同的职责,它们之间的关系密不可分。理解它们的区别和联系有助于更好地开发、部署和运行 Java 应用程序。对于 Java 开发者来说ÿ…...

Golang|工厂模式
工厂模式是一种创建型设计模式,它的核心思想是:把对象的创建过程封装起来,不直接在代码中 new 一个对象,而是通过一个“工厂”来生成对象。这样做的好处是: 降低了代码之间的耦合(依赖具体类减少࿰…...
的延迟约束优化)
Transformer数学推导——Q29 推导语音识别中流式注意力(Streaming Attention)的延迟约束优化
该问题归类到Transformer架构问题集——注意力机制——跨模态与多模态。请参考LLM数学推导——Transformer架构问题集。 在语音识别任务中,实时性是核心需求 —— 想象你使用语音助手时,每说完一个词就希望即时看到文字反馈,而不是等整句话说…...

dx11 龙书学习 第四章 dx11 准备工作
4.1 准备工作 Direct3D的初始化过程要求我们熟悉一些基本的Direct3D类型和基本绘图概念;本章第一节会向读者介绍些必要的基础知识。然后我们会详细讲解Direct3D初始化过程中的每一个必要步骤,并顺便介绍一下实时绘图应用程序必须使用的精确计时和时间测…...

运维打铁:域名详解及常见问题解决
文章目录 前言一、域名基础概念1. 什么是域名2. 域名结构3. 域名解析 二、域名工作原理1. DNS 服务器层次结构2. 域名解析过程 三、常见域名问题及解决办法1. 域名无法解析2. 域名解析延迟3. 域名解析结果不一致 四、总结 前言 在当今数字化的时代,互联网已经成为我…...

【大模型ChatGPT+R-Meta】AI赋能R-Meta分析核心技术:从热点挖掘到高级模型、助力高效科研与论文发表“
Meta分析是针对某一科研问题,根据明确的搜索策略、选择筛选文献标准、采用严格的评价方法,对来源不同的研究成果进行收集、合并及定量统计分析的方法,现已广泛应用于农林生态,资源环境等方面,成为Science、Nature论文的…...
:如何将一台电脑上的Elasticsearch服务迁移到另一台电脑上)
ElasticSearch深入解析(五):如何将一台电脑上的Elasticsearch服务迁移到另一台电脑上
文章目录 0.安装数据迁移工具1.导出数据2.导出mapping3.导出查询模板4.拷贝插件5.拷贝配置6.导入到目标电脑上 0.安装数据迁移工具 Elasticsearch dump是一个用于将Elasticsearch索引数据导出为JSON格式的工具。你可以使用Elasticsearch dump通过命令行或编程接口来导出数据。…...

QT中的多线程
Qt中的多线程和Linux中的线程本质是相同的,Qt中针对系统提供的线程API进行了重新封装 QThread类 Qt中的多线程一般通过QThread类实现,要想创建线程就要创建这个类的实例 QThread代表一个在应用程序中可以独立控制的线程,也可以和进程中的其…...

Win11安装Ubuntu20.04简记
写在前面 之前装的22.04,不稳定,把22.04卸载了,重新安装20.04系统。这里主要把卸载和安装的过程中参考到的博客在这记录一下。 卸载ubuntu系统参考的博文 卸载参考博文1 卸载参考博文2 Ubuntu20.04安装参考博文 安装参考博文1 安装参考博…...

电子电器架构 ---电气/电子架构将在塑造未来出行方面发挥啥作用?
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 钝感力的“钝”,不是木讷、迟钝,而是直面困境的韧劲和耐力,是面对外界噪音的通透淡然。 生活中有两种人,一种人格外在意别人的眼光;另一种人无论…...

pdf.js移动端预览PDF文件时,支持双指缩放
在viewer.html中添加手势缩放代码 <script>// alert("Hello World");let agent navigator.userAgent.toLowerCase();// if (!agent.includes("iphone")) {let pinchZoomEnabled false;function enablePinchZoom(pdfViewer) {let startX 0, start…...

机器人--激光雷达
教程 教程 激光雷达 激光 激光(Laser),是一种人造的、高度纯净的单色光。 雷达 激光器旋转机构雷达。 雷达根据激光探头发出激光束的数量,一般可以分为单线激光雷达(2D激光雷达)和多线激光雷(3D激光雷达)。 作用 测距原理 激…...

最新ios开发证书/发布证书/免费证书/企业证书制作教程
本文介绍了如何制作或者苹果开发证书p12文件,含开发证书,推送证书,发布证书,企业证书,免费证书,您在iphone和ipad开发构建 IOS App 应用和苹果ios app签名需要用到。如果嫌麻烦,可以使用懒人工具…...

【Keil5-开发指南】
Keil5-编程指南 ■ Keil5 介绍■ J-Flash 使用■ Keil5-Debug调试工具 Jlink---STLink---DAP仿真器■ Keil5 使用 AStyle插件格式化代码■ Keil5-编译4个阶段■ Keil5-Boot和APP配置■ Keil5-报错■ 芯片手册区别 ■ Keil5 介绍 Keil5 介绍 ■ J-Flash 使用 J-Flash 使用 ■…...

蓝桥杯 18. 机器人繁殖
机器人繁殖 原题目链接 题目描述 X 星系的机器人可以自动复制自己。它们用 1 年的时间可以复制出 2 个自己,然后就失去复制能力。 每年 X 星系都会选出 1 个新出生的机器人发往太空。也就是说,如果 X 星系原有机器人 5 个,1 年后总数是&a…...

从微服务到AI服务:Nacos 3.0如何重构下一代动态治理体系?
在现代微服务架构的浪潮中,Nacos早已成为开发者手中的“瑞士军刀”。作为阿里巴巴开源的核心中间件,它通过动态服务发现、统一配置管理和服务治理能力,为云原生应用提供了坚实的基石。从初创公司到全球500强企业,Nacos凭借其开箱即…...
Sentinel---高可用流量管理框架/服务容错组件)
60、微服务保姆教程(三)Sentinel---高可用流量管理框架/服务容错组件
Sentinel—高可用流量管理框架/服务容错组件 一.为什么要用Sentinel? 1.微服务架构中当某服务挂掉的时候常见的原因有哪些? 1.异常没处理 比如DB连接失败,文件读取失败等 2.突然的流量激增 比如:用户经常会在京东、淘宝、天猫、拼多多等平台上参与商品的秒杀、限时抢…...
