当前位置：首页 > news >正文

【数据结构】·励志大厂版（复习+刷题）：二叉树

news 来源：原创 2025/6/16 12:21:49

前引：哈喽小伙伴们！经过几个月的间隔，还是逃脱不了再次复习的命运！！！本篇文章没有冗杂的闲话，全是干货教学，带你横扫二叉树的几种遍历，怎么前序、、中序、后续？如何识别？二叉树其实难得就是它的递归，代码量其实并不多，插入与遍历打印都是递归，但是本篇文章完全就是buuff加身，看完还不会二叉树的欢迎在评论区留言，小编接受检讨！~~正文开始

知识点速览

树的名词解释

二叉树的四种遍历

二叉树性质：

满二叉树：

完全二叉树：

练习题（1）

练习题（2）

练习题（3）

练习总结

二叉树实现

定义结构体

初始化

新增节点

前序遍历

中序遍历

后序遍历

二叉树OJ（1）

二叉树OJ（2）

二叉树OJ（3）

二叉树OJ（4）

知识点速览

在学二叉树之前我们需要作为补充了解树的几个名词概念

树的名词解释

节点的度：一个节点含有子节点的个数。例如A的度：为6

叶节点或终端节点：度为0的节点。例如：B、C、H、P、Q、N都为叶节点

分支节点或非终端节点：度不为0的节点。例如：D、A、G、J都为分支节点

双亲节点或父节点：若一个节点有度（即有子节点），该节点为父节点。例如：A、D、E为父节点

孩子节点或子节点：也就是拥有度的这些节点的下一层节点。例如：B、C、D都为子节点

兄弟节点：拥有相同父节点的子节点。例如：I、J是兄弟节点，K、L、M是兄弟节点

树的度：孩子节点最多的度。例如：这棵树中孩子节点最多的是A节点，那么这颗树的度为6

节点的层次：从根节点开始从1开始算。例如：J的层次为3，Q的层次为4

树的高度或者深度：树中节点的最大层次。例如：这棵树节点层次最大的是P与Q，树最大层次为4

节点的祖先：从根节点到该分支的所有节点。例如：A是所有节点的祖先。G不是L的祖先

子孙：以某节点为根的子树中的任意节点。例如：所有节点是A的子孙。Q不是D的子孙

森林：由 m （m>0）棵互不相交的多棵树的集合称为森林

二叉树的四种遍历

这四种遍历其实并不难，下面小编带大家深刻理解这四种遍历！

首先前、中、后三种遍历中的的这三个关键字“前”“中”“后”都是根据根节点而言的，左子树永远在右子树前面，（大家注意观察根节点与遍历方式的位置！）它的遍历都是将一个子树对应位置遍历完之后再遍历又一个子树，理解：每次不断分成不同大小的树，然后递归到末尾，再原路返回。小编以中序遍历为列，仔细讲解一下！最好的理解方式就是动手画到不出错为止！

前序遍历：根节点、左子树、右子树

遍历顺序：A->B->D->NULL->NULL->E->NULL->NULL->C->NULL->F->NULL->NILL

中序遍历：左子树、根节点、右子树

以A为根节点，先访问左子树，也就是这部分

再以B为根节点，再访问左子树，也就是这部分

再以D为根节点，访问其左子树，已经是这部分

此时已经到底了无法再分，访问“NULL”，然后访问根节点“D”，再访问D的右子树 “NULL”

以此类推，直到不能分为止，这里是利用了递归到NULL就返回的原理。

遍历顺序：NULL->D->NULL->B->NULL->E->NULL->A->NULL->C->NULL->F->NULL

后序遍历：左子树、右子树、根节点

遍历顺序：NULL->NULL->D->NULL->NULL->E->B->NULL->NULL->NULL->F->C->A

层序遍历：一层一层访问

遍历顺序：A->B->C->D->E->NULL->F->NULL->NULL->NULL->NULL->NULL->NULL

二叉树性质：

满二叉树：

概念：每个父节点除最后一层的叶子节点外都有两个子节（满二叉树是一种特殊的完全二叉树）

性质（1）： 假设根节点层数为0，树层数为K，那么它的节点个数N为 2^K-1，高度为 logN

推论：第一层有1个节点（2^0），第二层有2个节点（2^1），第三层有4个节点（2^2），以此类推，得到节点数 N = 2^0 + 2^1 + 2^2 + 2^3 + ...... = 2^K -1 . 此时 K = log（N+1）

性质（2）：假设根节点层数为0，二叉树第 K 层的节点数最多为 2^K 个

性质（3）：任意一棵二叉树，假设度为 0 的节点数为 n0 ，度为 2 的节点数为 n2 ,满足以下关系

满足 n0 = n2+1（只记结论）

例如：假设现在有这样一棵树，度为0的节点数有5个，度为2的节点数有4个，满足 5=4+1

完全二叉树：

概念：只有最后一层不满，且最后一层从左到右是连续的

性质：节点总数 N 满足 N < 2^K-1 ，高度 K =log（N+1）

推论：我们无法确定完全二叉树具体的节点个数，只能通过满二叉树进行推理，其它树亦如此

练习题（1）

套用公式：度为0的节点数（叶子节点）= 度为2的节点数 + 1 ，得到最终答案 200

练习题（2）

这是一棵完全二叉树，它的节点组成是度为0的、度为1的、度为2的总和，也就是：

x0 + x1 + x2 =2n ，同时套用公式 x0 = x2 + 1，两个结合得到：2 * x0 + x1 - 1 = 2n

我们观察图，发现完全二叉树度为1的节点只有一个，因此 x1 = 1，那么算出来得到 x0 = n

练习题（3）

我们假设高度为 h ，最后一层缺了 x 个，同时知道满二叉树是特殊的完全二叉树

那么满足： 2^h-1 - x = 531. 同时 x 的范围应该在【0，2 ^ h-1】，x 的范围如下图所示：

直接一个都不缺，为0个

最多缺一个，x为2 ^ h-1个

结合这两个关系式，去套，最后得出只有当高度为10时满足（注意这里的层数从0开始）

练习总结

除了直接套用公式的题，如果出现节点总数求某个变量的值，似乎都要去通过建立方程表示节点总数，表示方式一般有两种：（1）不同度的节点数之和（2）通过节点总数满二叉树计算公式去计算

二叉树实现

定义结构体

咱们按照二叉树的结构，定义一个左子节点、右子节点、一个数据域就行了，这是最简单的定义

//重定义类型
typedef int Datatype;typedef struct Tree
{//左孩子节点struct Tree* left;//右孩子节点struct Tree* right;//数据域Datatype data;
}Tree;

初始化

初始化我们开辟一个根节点返回就行了，以后将其作为参数再去连接左右节点

//初始化树
Tree* Perliminary(Datatype data)
{//开辟根节点Tree* newnode = (Tree*)malloc(sizeof(Tree));//判断有效性if (newnode == NULL){printf("节点开辟失败\n");return NULL;}//初始化指针newnode->data = data;newnode->left = NULL;newnode->right = NULL;return newnode;
}

新增节点

首先我们初始化了一个根节点，新增的节点值与根节点的值进行比较

如果小于根节点的值，递归左子树；如果大于根节点的值，递归右子树；

随着递归的不断调用，它的根节点会不断改变，如果为空，就返回新增的节点

最后回到最初的根节点

//新增节点
Tree* Capacity(Tree* TreeNode, Datatype data)
{//如果是空节点就插入if (TreeNode == NULL){return Perliminary(data);}//如果是非空节点就继续递归//较小就插入到左子节点if (data < TreeNode->data){TreeNode->left = Capacity(TreeNode->left, data);}elseTreeNode->right = Capacity(TreeNode->right, data);//回到原初的根节点return TreeNode;
}

前序遍历

首先递归到子树的极端，遇到空就开始返回，再调整打印顺序

//前序遍历
Tree* Preorder(Tree* TreeNode)
{if (TreeNode == NULL){return;}//根节点printf("%d ", TreeNode->data);//左子树Preorder(TreeNode->left);//右子树Preorder(TreeNode->right);
}

中序遍历

//中序遍历
Tree* Mid(Tree* TreeNode)
{//如果遇到空返回if (TreeNode == NULL){return;}//左子树Mid(TreeNode->left);//根节点printf("%d ", TreeNode->data);//右子树Mid(TreeNode->right);
}

后序遍历

//后序遍历
Tree* Behind(Tree* TreeNode)
{//递归到深处，如果是空就开始返回if (TreeNode == NULL){return;}//左子树Behind(TreeNode->left);//右子树Behind(TreeNode->right);//根printf("%d ", TreeNode->data);
}

二叉树OJ（1）

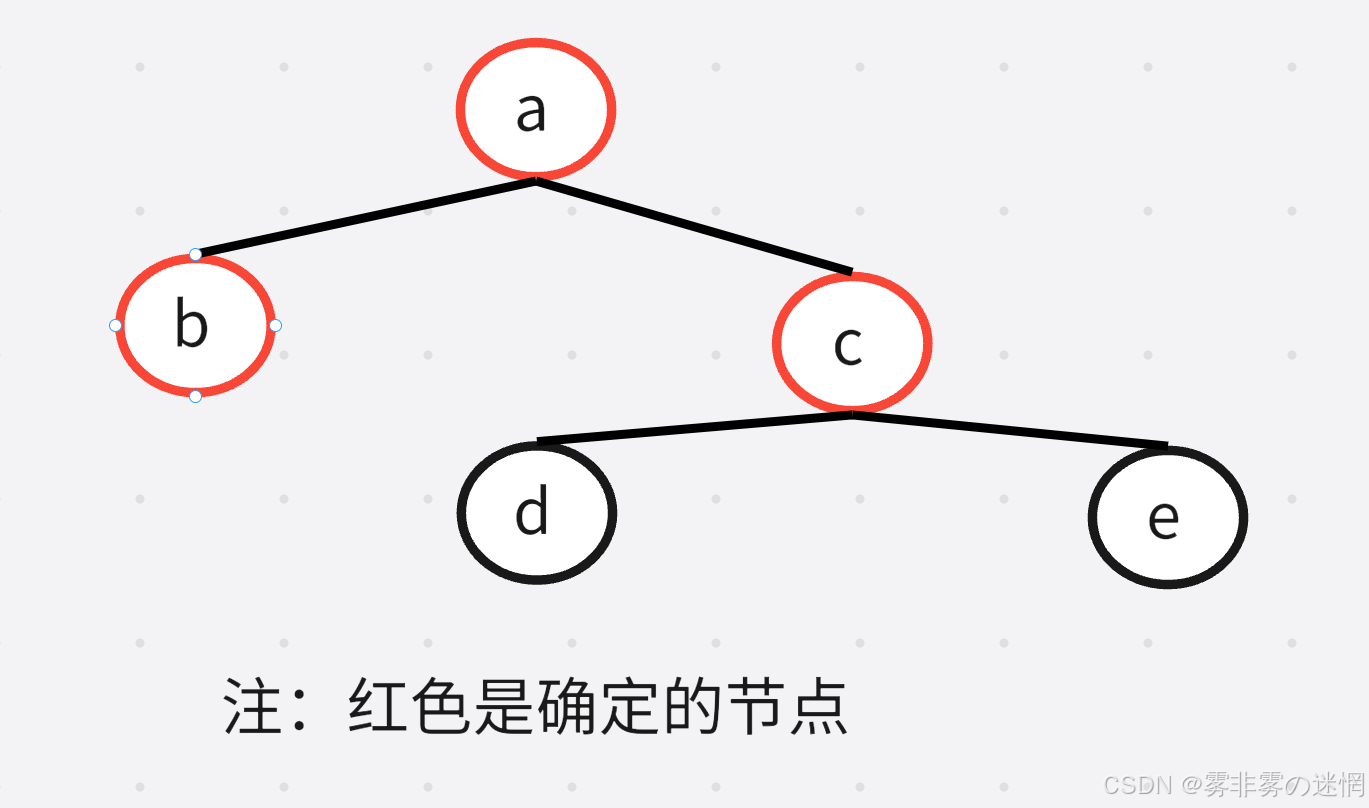
假设现在有这样一棵树

它的中序遍历结果为：D->B->E->A->F->C 后序遍历结果为：D->E->B->F->C->A

按照中序顺序，我们去推得到 b 应该在最左边；按照后序顺序，我们得到 a 应该是根节点

所以 a 是在根节点，再根据中序顺序，得到 a 的左边是 b ，同时 c 是 a 的右子树，这样就能推出

二叉树OJ（2）

题目链接：https://leetcode.cn/problems/binary-tree-preorder-traversal

题目是要我们将前序遍历的节点结果返回

思维讲解：

流程：用一个空间将每次遍历的值存储起来，然后返回

（1）首先我们开辟数组，数组的空间大小最好是由节点个数决定，因此先遍历二叉树计算节点

return root==NULL? 0 : treesize(root->left) + treesize(root->right) + 1;

（2）然后开辟对应大小的数组空间

   //计算节点个数int size=treesize(root);//开辟空间int* arr=(int*)malloc(sizeof(int)*size);

（3）接下来就是递归遍历储存节点，但是要考虑一个问题，如果在这个函数里面去递归，那么每次调用都要去开辟空间，所以我们选择再开一个来进行递归遍历，参数是根节点、空间指针、计数

注意：计数的 i 应该取地址，因为递归会开辟多个函数，不然每次 i 都只是一次拷贝而已

  //存进空间int i=0;preorder_Traversal(root,arr,&i);

（4）然后将之前的前序遍历的打印换成储存即可

 //前序遍历if(root==NULL){return;}arr[*i]=root->val;++(*i);preorder_Traversal(root->left,arr,i);preorder_Traversal(root->right,arr,i);

（5）最后：这是整型指针空间，返回的只是一个元素，所以按照题目要求，还有设置元素个数

 *returnSize = size;return arr;

二叉树OJ（3）

题目链接：https://leetcode.cn/problems/binary-tree-postorder-traversal

此题和上面这题几乎一模一样，就作为思维训练巩固给大家了！记得独立完成哦！

二叉树OJ（4）

题目链接：https://leetcode.cn/problems/maximum-depth-of-binary-tree

思维讲解：此题是求二叉树的最大深度，二叉树最大深度就是最大层数

（1）假设有一棵树如上图，它的深度是3。这里采用分治思想，先求左子树的深度为3，再求右子树的深度为2，再对比找最大值，然后返回最大值+1（因为一个节点层次为1）

（2）下面我们来实现，先递归左子树，再递归右子树，那么它是如何计算子树深度的呢？

假设递归到左子树的末尾，q 的左子树右子树都为空，返回0，此时0>0为假，返回0+1

那么q拿到的就是1

假设递归到 c ，c的左右子树都不为空，继续递归，此时d的左右子树都为空返回,0>0为假d拿到1

同理，e拿到1；1>1为假，c拿到的就是1+1。其它节点类推即可

小编期待与你的下次相遇！

知识点速览

树的名词解释

二叉树的四种遍历

二叉树性质：

满二叉树：

完全二叉树：

练习题（1）

练习题（2）

练习题（3）

练习总结

二叉树实现

定义结构体

初始化

新增节点

前序遍历

中序遍历

后序遍历

二叉树OJ（1）

二叉树OJ（2）

二叉树OJ（3）

二叉树OJ（4）

相关文章：