当前位置：首页 > news >正文

神经网络与深度学习第四章-前馈神经网络

news 来源：原创 2025/6/17 10:40:24

前馈神经网络

在本章中，我们主要关注采用误差反向传播来进行学习的神经网络。

4.1 神经元

神经元是构成神经网络的基本单元。主要是模拟生物神经元的结构和特性，接收一组输入信号并产生输出。
现代神经元中的激活函数通常要求是连续可导的函数。
图片是书上的（邱锡鹏）

净输入代表了输入信号对神经元的总和刺激强度，是激活函数的输入值。净输入可以：①决定神经是否激活；②反映输入信号的整合效果。

在这里插入图片描述
激活函数。为了增强网络的表示能力和学习能力，激活函数需要具备以下几点性质：
（1）连续且可导（允许在少数点上不可导）的非线性函数。可导的激活函数可以直接利用数值优化的方法（比如梯度下降法）来学习网络参数。
（2）激活函数及其导函数尽可能简单，可以提高网络计算效率。
（3）激活函数的导函数的值域要在一个合适的区间内，否则会影响训练的效率和稳定性。
在这里插入图片描述

4.1.1 Sigmoid型函数

Sigmoid型函数是指一类S型曲线函数，是两端饱和函数。常用的该类型函数是Logistic函数和Tanh函数。

对于函数 f(x) ,若x -> 负无穷 时，其导函数 f'(x)->0,则称其为左饱和；若x -> 正无穷 时，其导函数 f'(x)->0,则称其为右饱和；当同时满足左右饱和时，称为两端饱和。

在这里插入图片描述
Logistic函数类似于一个“挤压”函数，把一个实数域的输入“挤压”导（0，1）。
当输入值在0附近时，Sigmoid型函数近似于线性函数；
当输入值靠近两端时，对输入进行抑制。输入越小，越接近于0；输入越大，越接近于1.
在这里插入图片描述
和感知器使用的阶跃激活函数相比，Logistic函数是连续可导的，数学性质更好。

所以装备了Logistic激活函数的神经元具有以下性质：
①其输出直接看作改良版分布，使得神经网络可以更好统计和学习模型进行结合；
②其可以看作一个软性门，用来控制其他神经网络输出信息的数量。
在这里插入图片描述

对比两个函数的形状，Tanh函数的输出是零中心化的，但是Logistic函数的输出恒大于0，非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移，进一步使得梯度下降的收敛速度变慢。

零中心化：函数输出值的均值为0（即对称于原点）。Tanh函数的输出范围是（-1，1）。均值为0；

4.1.1.1 Hard-Logistic函数和Hard-Tanh函数

Logistic函数和Tanh函数计算开销大。因为这两个函数在0附近近似线性，两端饱和。所以，这两个函数可以通过分段函数来近似。
在这里插入图片描述

4.1.2 ReLU函数

ReLU（修正线性单元），是目前神经网络中经常使用的激活函数。实际上是一个斜坡函数。
定义为：
在这里插入图片描述
优点：
①计算高效：采用ReLU的神经元是需要进行加、乘、比较的操作；
②该函数具有生物学合理性，有单侧抑制，宽兴奋边界。
Sigmoid型激活哈桑农户会导致一个非稀疏的神经网络，但是ReLU却具有很好的稀疏性，大约50%的神经元会处于激活状态。
③ReLu函数是左饱和函数，当x > 0 时导数为1，在一定程度上缓解了神经网络的梯度消失问题，加速下降的收敛速度。
缺点：
①ReLU函数的输出是非零中心化的，给后一层的神经网络引入偏置偏移，影响下降的效率。
②ReLU神经元在训练时容易死亡。在训练时，若参数在一次不恰当的更新后，第一个隐藏层中的某个ReLu神经元在所有的训练数据上都不能被激活，会使得该神经元自身参数的梯度永远时0，在以后的训练中也永远不能被激活。这种现象是死亡ReLU问题，也可能发生在其他隐藏层。

4.1.2.1 带泄露的ReLU

带泄露的ReLU 在输入x < 0 时，保持一个很小的梯度。这样当神经元非激活时也能有一个非零的梯度可以更新参数，避免永远不能被激活。
传统的ReLU问题：当输入为负时，梯度为0，导致神经元可能永久死亡。LeakyReLU可以解决这个问题。
加粗样式
在这里插入图片描述

4.1.2.2 带参数的ReLU

带参数的ReLU引入一个可学习的参数。不同神经元可有不同参数。
在这里插入图片描述

其中α是x <= 0 时函数的斜率。因此，PReLU时非饱和函数，若α = 0，则PReLU会退化为ReLu。若α是一个很小的常数，则PReLU可以看作是带泄露的ReLU。
在这里插入图片描述

4.1.2.3 ELU函数

ELU（指数线性单元），是一个近似的零中心化的非线性函数。
在这里插入图片描述

4.1.2.4 Softplus函数

Softplus函数可以看作是ReLU的平滑版本。
在这里插入图片描述
Softplus函数其导数刚好是Logistic函数。没有稀疏激活性。
下面是ReLU、Leaky ReLU、ELU、Softplus 的形状对比

下面是ReLU、Leaky ReLU、ELU、Softplus 的梯度对比

4.1.3 Swish函数

Swish函数是一种自门控激活函数。
在这里插入图片描述
当σ(βx)接近于1时，门处于“开”状态，激活函数的输出近似于x本身。当σ(βx)接近于0时，门的状态为“关”，激活函数的输出近似于0；

当β = 0时，Swish函数变成线性函数。当β = 1时，Swish函数在x > 0时近似线性，在x < 0 时近似饱和，同时具有一定的非单调性。当β -> 正无穷时，σ(βx) 趋向于离散的0-1函数，Swish函数近似于ReLU函数。因此，Swish函数可以看作线性函数和ReLU函数之间的非线性插值函数，其程度由参数β控制。

4.1.4 GELU函数

GELU（高斯误差线性单元）是一种通过门控机制来调整其输出值的激活函数，和Swish函数类似。
其核心思想是将输入 x 与高斯分布的累积分布函数（CDF）结合。公式为：
在这里插入图片描述

特点：
①通过输入值 x 在高斯分布中的概率来“门控”输出，实现非线性变换。
②高斯分布的CDF是S型函数，因此GELU具有平滑的非线性特性。

由于高斯分布的累积分布函数为S型函数，所以，GELU函数可以用Tanh函数或Logistic函数近似。
在这里插入图片描述
3. 与Swish函数的关系

Swish函数定义为 Swish(x)=xσ(βx)，其中 β 是可学习参数。
当GELU用Sigmoid近似且系数 β=1.702 时，两者形式一致。因此，GELU是Swish的一种特殊情形。

4.与其他激活函数的对比

ReLU：GELU在负值区域非零，允许少量负值信息通过，避免“死神经元”。
Swish：GELU的理论基础更明确（基于高斯分布），而Swish更通用（参数可调）。

在这里插入图片描述

4.1.5 Maxout单元

Maxout 单元是一种分段线性激活函数
其核心特点是：

输入为向量：不同于传统激活函数（如 ReLU、Sigmoid）接收标量输入，Maxout 的输入是上一层神经元的全部原始输出向量
x=[x 1,x 2,…,x D]。
多组线性变换：通过 K 组独立的权重向量 w k 和偏置 b k，生成 K 个候选线性输出 z k。
取最大值输出：最终输出是这 K 个候选值中的最大值，即 maxout(x)=max(z 1 ,z 2,…,z K )。
在这里插入图片描述

4.2 网络结构

人工神经网络主要由大量得神经元以及它们之间得有向连接构成。因此考虑三方面：
①神经元得激活规则：
主要是指神经元输入到输出之间的映射关系，一般为非线性连接。
②网络的拓扑结构：
不同神经元之间的连接关系
③学习算法：
通过训练数据来学习神经网络的参数。
目前常用的网络结构有三种：

4.2.1 前馈网络

前馈网络中各个神经元按接受信息的先后分为不同的组。每一组都可以看成是一个神经层。每一层中的神经元接收前一层神经元的输出，并输出到下一层神经元。
整个网络中的信息是朝一个方向传播。并且前馈网络是无反馈连接：数据从输入层逐层传递到输出层，没有环路或反向传播路径（区别于循环神经网络RNN）。
2. 典型结构
①全连接前馈网络（Fully Connected Feedforward Network）：
每一层的神经元与下一层的所有神经元相连。
例如：多层感知机（MLP）。
②卷积神经网络（CNN）：
通过局部连接（卷积核）和权值共享减少参数，适合处理网格数据（如图像）。
在这里插入图片描述

4.2.2 记忆网络

1.核心定义
记忆网络（也称反馈网络）是一类具有记忆功能的神经网络，其特点是：

①动态状态：神经元可接收自身或其他神经元的历史信息，状态随时间变化。
②循环结构：信息传播可以是单向循环（如RNN）或双向交互（如玻尔兹曼机），结构上表现为有向循环图或无向图。
③外部记忆扩展：通过引入外部存储单元（如神经图灵机），显式增强网络的记忆容量。

2.典型模型

模型名称	特点
①循环神经网络（RNN）	通过隐藏状态传递历史信息，适合处理时序数据（如文本、语音）。
②Hopfield网络	能量模型，通过无向连接实现联想记忆，用于优化和模式恢复。
③玻尔兹曼机（BM）	概率生成模型，含隐藏层和可见层，通过随机采样学习分布。
④受限玻尔兹曼机（RBM）	概率生成模型，含隐藏层和可见层，通过随机采样学习分布。
⑤神经图灵机（NTM）	引入外部记忆矩阵和读写头，模拟计算机的存储机制。

4.2.3 图网络

1.核心定义
图网络是专门处理图结构数据的神经网络，其特点包括：
①输入形式：数据以图（Graph）形式表示，包含节点（Nodes）、边（Edges）和全局属性。
②泛化能力：是前馈网络和记忆网络的泛化，可处理非欧几里得数据（如社交网络、分子结构）。
③信息传递机制：节点通过聚合邻居信息更新自身状态（消息传递）。
2.典型模型

模型名称	核心机制
①图卷积网络（GCN）	通过邻接矩阵归一化聚合邻居信息
②图注意力网络（GAT）	引入注意力机制，动态学习邻居节点的重要性权重
③消息传递神经网络（MPNN）	通用框架，分“消息传递”和“状态更新”两步

在这里插入图片描述
神经网络是一种连接主义模型，也就是PDP(Parallel Distributed Processing)模型（PDP（并行分布式处理）模型是连接主义道德一种实现形式）。
它具有以下关键特征：

信息表示的分布式特性
分布式存储：信息不是局部存储在单个单元中，而是分散在整个网络的连接权重模式中

叠加存储：同一组神经元可以同时存储多个记忆或模式

内容寻址：可以通过部分信息恢复完整模式(联想记忆)

并行处理机制
大规模并行性：所有处理单元同时进行计算

集体计算：结果由大量简单单元的协同活动决定

非线性交互：单元间通过非线性函数相互作用

连接权重的重要性
知识存储在连接中：系统的"知识"体现在单元间的连接权重上

可塑性：连接权重可通过学习调整(如Hebbian学习规则)

适应性：系统能通过调整权重适应新任务

处理单元的特性
简单处理单元：每个单元只执行简单计算(如加权求和+激活函数)

非符号性：单元活动不直接对应符号或概念

数值性：信息表示为连续的激活值而非离散符号
与符号主义的对比

特性	PDP/连接主义模型	符号主义模型
信息表示	分布式(连接权重模式)	局部(离散符号)
处理方式	并行	串行
知识存储	隐式(难以解释)	显式(可解释)
学习方式	参数自动调整	规则手工编码
容错性	强	弱

4.3 前馈神经网络（全连接神经网络，多层感知器）

各神经元分别属于不同层，层内无连接
相邻两层间的神经元全部两两连接
整个网络中无反馈，信号从输入层向输出层单向传播，可用有向无环图表示。

注意： ①神经网络的层数一般不包括输入层，只计算隐藏层和输出层。
②神经网络的层数、第l层神经元的个数、第l层神经元的激活函数这些都是超参数。

注意： ①第一个公式地本质是仿射变换。
对于向量空间中的点 x ∈ ℝⁿ，仿射变换可表示为：T(x) = Wx + b

仿射变换是线性变换的扩展，由线性变换和平移变换组合而成

前馈计算：
**加粗样式**

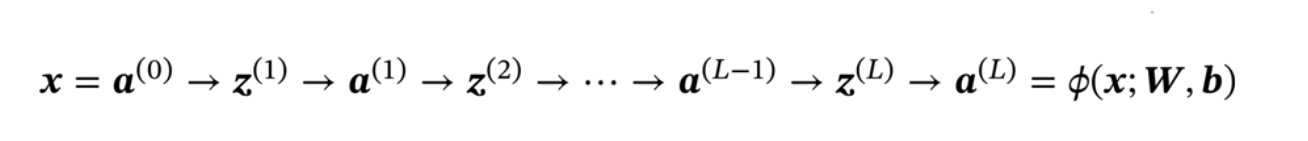
4.3.1 通用近似定理

（理论不做过多解释）
结论：
**通用近似定理说明了：**神经网络的计算能力可以去近似一个给定的连续函数

4.3.2 应用到机器学习

在这里插入图片描述

4.3.4 参数学习

1.交叉熵损失函数：ℒ(y, ŷ) = -yᵀlog(ŷ)

y：one-hot编码的真实标签（如[0,1,0]表示第二类）
ŷ：模型预测的概率分布（如[0.1,0.7,0.2]）
物理意义：当预测概率ŷ与真实标签y差距越大，损失值越高

2.结构化风险函数：ℛ(W,b) = (1/N)∑ℒ(y⁽ⁿ⁾,ŷ⁽ⁿ⁾) + (1/2)λ‖W‖²_F（学习准则）

第一项：所有样本的平均交叉熵损失
第二项：L2正则化（权重衰减），控制模型复杂度
λ：调节正则化强度的超参数（λ越大惩罚越重）

3.网络参数通过梯度下降法进行学习，每次迭代中，第 l 层的参数更新方式：

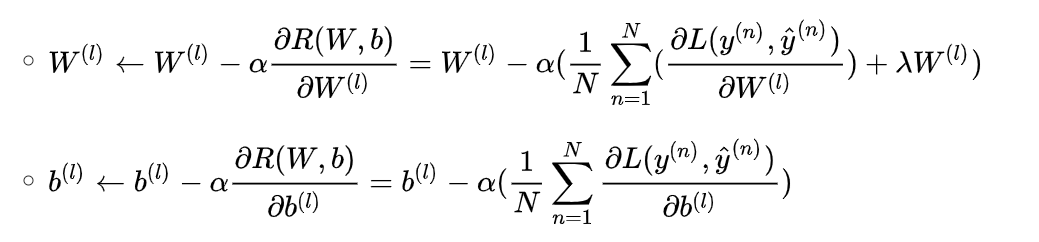
α是学习率。使用反向传播算法来高效地计算梯度。
一种更通用的计算梯度算法是：自动微分

4.4 反向传播算法

在这里插入图片描述

分母布局是列向量，分子布局是行向量。

用随机梯度下降法进行参数学习，需要计算损失函数关于每个参数的梯度
在这里插入图片描述
上面的公式将利用链式法则进行展开。
链式法则：

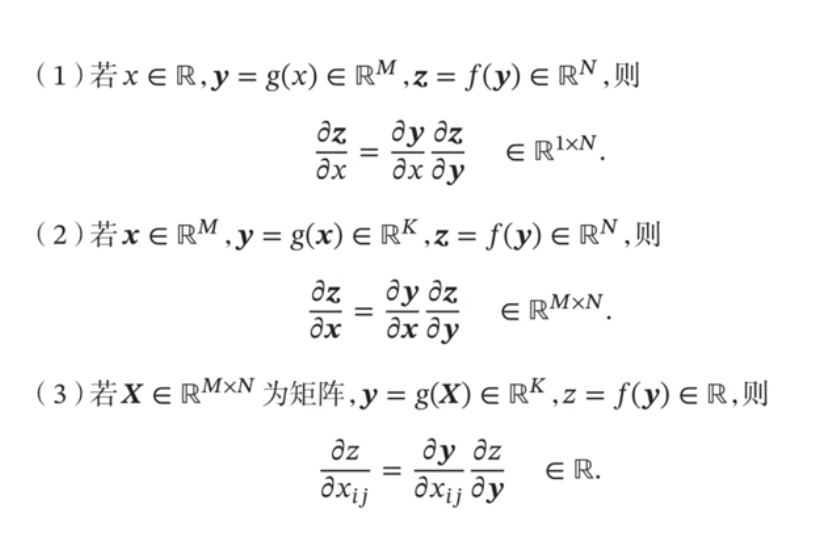
情况1：向量对标量的链式求导
情况2：向量对向量的链式求导
情况3：标量对矩阵的求导
根据上面偏导数的公式，得到求3个偏导数式子即可。

在这个式子中，z是列向量，w(ij)是标量，所以求导结果是一个行向量。只有z(i)对w(ij)的求导不为0，是因为
第二个偏导数：（反向传播）

**fl(.)**是按位函数

第三个偏导数：
在这里插入图片描述
使用误差反向传播算法的前馈神经网络训练过程有以下步骤：
①前馈计算每一层的净输入和激活值，直到最后一层；
②反向传播计算每一层的误差项。（就是求第2个偏导数）；
③最后计算每一层参数的偏导数，并更新参数（就是求第1个和第3个偏导数，之后再按照4.3.3 参数学习里面的第3部分进行参数更新）。

按照上面的式子，代入到损失函数关于每个参数的梯度的式子中，得到：
在这里插入图片描述

4.5 计算图和自动微分

（其实还有数值微分和符号微分，这里不再写，大家可以自行了解）
1.自动微分是一种可以对一个（程序）函数进行计算导数的方法

处理的对象是一个函数或一段程序
是目前大多数深度学习框架的首选
基本原理：所有的数值计算可以分解为一些基本操作，包括 + 、-、*、/ 和一些初等函数 exp、log、sin、cos等，并构成一个计算图，然后用链式法则来自动计算一个复合函数的梯度
无需事先编译，在程序运行阶段边计算边记录计算图，计算图上的局部梯度都直接代入数值进行计算，然后用前向模式或反向模式计算最终的梯度。

2.自动微分分为：

前向模式：按计算图中计算方向的相同方向来递归地计算梯度
反向模式：按计算图中计算方向的相反方向来递归地计算梯度
反向模式和反向传播的计算梯度的方式相同。

在这里插入图片描述

3.为什么神经网络选择反向模式？
- 输出为标量：损失函数 R 的输出维度 M = 1，反向模式仅需 1次计算。
- 参数规模大：输入维度 N（参数量）极大，前向模式需要 N 次计算，效率极低。
- 链式法则优化：反向传播利用动态规划思想，避免重复计算中间变量的梯度。
（上面的两张图就是解释这个问题的）
如果函数和参数之间有多条路径，可以将这多条路径上的导数再进行相加，得到最终的梯度。
4.反向传播算法（自动微分的反向模式）
前馈神经网络的训练过程可以分为以下3步：
①前向计算每一层的状态和激活值，直到最后一层；
②反向计算每一层的参数和偏导数；
③更新参数。（其实跟4.4 反向传播算法里面介绍的是一样的，只不过是用这里提到的前向计算和反向计算再表述一遍）
5.计算图按构建方式可分为：
①静态计算图：在编译时构建计算图，构建好后在程序运行时不能改变
特性：构建时可以进行优化，并行能力强，但灵活性比较差
实例：Tensorflow
②动态计算图：在程序运行时动态构建
特性：不容易优化，难以并行计算，但灵活性比较高
实例：Pytorch、Tensorflow 2.0

6.Keras使用展示
展示如何使用Keras（一个高级神经网络API）在30秒内快速构建并训练一个简单的全连接神经网络。

from keras.models import Sequential  
from keras.layers import Dense, Activation  
from keras.optimizers import SGD
#1.导入必要的模块.Sequential: 线性堆叠模型，用于构建层与层之间简单连接的神经网络；Dense: 全连接层；Activation: 激活函数层；SGD: 随机梯度下降优化器
model = Sequential()
#2.创建一个空的顺序模型，后续可以逐层添加网络结构
model.add(Dense(output_dim=64, input_dim=100))  
model.add(Activation("relu"))  
model.add(Dense(output_dim=40))  
model.add(Activation("softmax"))
#3.构建了一个两层的全连接神经网络：
#第一层:输入维度: 100 (input_dim=100)；输出维度: 64 (output_dim=64)；使用ReLU激活函数
#第二层:输出维度: 40 (自动继承上一层的64作为输入)；使用Softmax激活函数（适用于多分类问题）
model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
#4.编译模型
#配置模型的学习过程：loss: 使用分类交叉熵损失函数（适用于多分类问题）；optimizer: 使用随机梯度下降(SGD)优化器 ；metrics: 在训练过程中监控准确率(accuracy)
model.fit(X_train, Y_train, nb_epoch=5, batch_size=32)
#5.训练模型
#X_train: 训练数据特征 ；Y_train: 训练数据标签 ；nb_epoch=5: 训练5个完整周期（整个数据集迭代5次）；batch_size=32: 每次梯度更新使用32个样本
loss = model.evaluate(X_test, Y_test, batch_size=32)
#6.评估模型

4.6 优化问题

神经网络的参数学习比线性模型要更加困难，主要原因有两点：
①非凸优化问题
②梯度消失问题

4.6.1 非凸优化问题

神经网络的优化问题是一个非凸优化问题
以下面最简单的两层
在这里插入图片描述
（可视化这里的代码优点问题，跑出来的图不太对…）

上述可视化结果分析

平方误差损失曲面特征：
①存在多个局部极小点
②损失曲面较为"平缓"
③梯度变化相对均匀
交叉熵损失曲面特征：
①同样存在多个局部极小点
②在y接近0的区域梯度变化剧烈
③整体形状更为"陡峭"

4.6.2 梯度消失问题/梯度弥散问题

在这里插入图片描述
**减轻梯度消失问题的方法：**使用导数比较大的激活函数，eg. ReLU

4.7 总结

在这里插入图片描述

前馈神经网络

4.1 神经元

4.1.1 Sigmoid型函数

4.1.1.1 Hard-Logistic函数和Hard-Tanh函数

4.1.2 ReLU函数

4.1.2.1 带泄露的ReLU

4.1.2.2 带参数的ReLU

4.1.2.3 ELU函数

4.1.2.4 Softplus函数

4.1.3 Swish函数

4.1.4 GELU函数

4.1.5 Maxout单元

4.2 网络结构

4.2.1 前馈网络

4.2.2 记忆网络

4.2.3 图网络

4.3 前馈神经网络（全连接神经网络，多层感知器）

4.3.1 通用近似定理

4.3.2 应用到机器学习

4.3.4 参数学习

4.4 反向传播算法

4.5 计算图和自动微分

4.6 优化问题

4.6.1 非凸优化问题

4.6.2 梯度消失问题/梯度弥散问题

4.7 总结

相关文章：