当前位置：首页 > news >正文

图像处理——边缘检测

news 来源：原创 2025/6/19 2:05:19

1 概述

边缘检测是图像处理和计算机视觉中的一项基本技术，用于识别图像中亮度变化剧烈的像素点，这些像素点通常对应于物体的边界。它通过检测图像中亮度或颜色变化显著的区域，提取出物体的轮廓，常用于计算机视觉、图像处理和模式识别等领域。

边缘检测的原理是通过计算图像中每个像素点与其周围像素点的亮度或颜色差异来确定该像素点是否为边缘。通常使用卷积操作来实现边缘检测，通过计算像素点与其周围像素点的差异来判断该像素点是否为边缘。

判断边缘的方法很多，基本上分为两类：

基于搜索的方法: 基于搜索的边缘检测方法首先计算边缘强度，通常用一阶导数表示，例如梯度模;然后，用计算估计边缘的局部方向，通常采用梯度的方向，并利用此方向找到局部梯度模的最大值。
基于零交叉的方法: 基于零交叉的方法找到由图像得到的二阶导数的零交叉点来定位边缘.通常用拉普拉斯算子或非线性微分方程的零交叉点。

而具体到实际场景中，具体的步骤为：

平滑图像: 减少噪声，噪声可能会被误认为是边缘。常用的平滑滤波器包括高斯滤波器。
计算导数: 计算图像中每个像素点的导数。根据导数的大小和方向，可以确定边缘的方向和强度。
非极大值抑制: 细化边缘，只保留梯度方向上的局部最大值。
阈值处理: 使用阈值来区分边缘像素和非边缘像素。

2 不同的边缘检测算法类型

2.1 一阶算子

一阶算子是一种基于图像梯度的边缘检测方法，它通过计算图像灰度值的一阶导数来检测边缘，即利用像素灰度值的变化率来找到边缘位置。一阶算子通过梯度的大小和方向来确定边缘的位置和方向。其中：

梯度：图像梯度表示灰度值在空间中的变化率，是一阶导数的体现。
梯度大小：梯度大小表示边缘的强度，是梯度的模。梯度值大的区域通常对应图像中的边缘。
梯度方向：梯度方向表示边缘的方向，是梯度的方向。

图像的一阶梯度计算比较简单：
$\begin{aligned} G_x(x, y) &= I(x+1, y) - I(x, y) \\ G_y(x, y) &= I(x, y+1) - I(x, y) \end{aligned}$
其中， $I (x, y)$ 表示图像的灰度值， $G_x(x, y)$ 和 $G_y(x, y)$ 分别表示图像在 $x$ 和 $y$ 方向上的梯度。梯度的方向为：
$\theta(x, y) = \arctan{\frac{G_y(x, y)}{G_x(x, y)}}$
梯度的大小为：
$\sqrt{G_x(x, y)^2 + G_y(x, y)^2}$

常见的一阶算子包括Sobel算子、Prewitt算子、Roberts算子等。

优点：
- 计算简单，速度快。
- 能够有效检测边缘位置。
- Sobel 算子等加入平滑操作，抗噪声能力较强。
缺点：
- 对噪声较为敏感（尤其是 Prewitt 和 Roberts 算子）。
- 边缘定位精度不高，容易丢失细节。

2.2 二阶算子

二阶算子是一种基于图像灰度值的二阶导数的边缘检测方法，它通过计算图像灰度值的二阶导数来检测边缘，即利用像素灰度值的变化率的变化率来找到边缘位置。二阶算子通过拉普拉斯算子来计算图像的二阶导数，然后通过阈值处理来确定边缘的位置和方向。二阶算子的计算公式为：
$\nabla^2 I(x, y) = \frac{\partial^2 I(x, y)}{\partial x^2} + \frac{\partial^2 I(x, y)}{\partial y^2}$
其中， $I (x, y)$ 表示图像的灰度值， $L (x, y)$ 表示图像的拉普拉斯算子。拉普拉斯算子是一个二阶导数算子，它可以检测图像中的边缘。

优点：
- 能够有效检测边缘位置。
- 对噪声较为敏感。
- 能够检测出图像中的细节。
缺点：
- 计算复杂，速度慢。
- 对噪声较为敏感。

常见的边缘检测算法包括Sobel算子、Prewitt算子、Canny算子等。

3 传统算法

3.1 Sobel算子

Sobel 算子通过计算图像在水平和垂直方向上的梯度来寻找图像中的边缘。梯度代表了图像中亮度变化的强度和方向，边缘通常对应于梯度较大的地方。Sobel 算子使用两个 3x3 的卷积核，分别用于计算水平方向 (Gx) 和垂直方向 (Gy) 的梯度。这两个卷积核如下：

水平方向 (Gx):

[-1 0 1-2 0 2-1 0 1]

垂直方向 (Gy):

[-1 -2 -10  0  01  2  1]

Sobel算子的特点:

简单易实现: Sobel 算子的计算过程相对简单，容易在各种图像处理平台上实现。
考虑了像素距离的影响: Sobel 算子在计算梯度时，对中心像素周围的像素赋予了不同的权重，更靠近中心像素的权重更高，这使得 Sobel 算子对噪声具有一定的抑制作用。
对噪声敏感: 虽然 Sobel 算子具有一定的抗噪能力，但仍然对噪声比较敏感。在处理噪声较大的图像时，通常需要先进行平滑处理，例如使用高斯滤波器。
能够检测水平和垂直方向的边缘: Sobel 算子能够同时检测图像中水平和垂直方向的边缘。
计算量相对较小: 相对于其他一些更复杂的边缘检测算法，Sobel 算子的计算量较小，适合对实时性要求较高的应用。

import cv2
import numpy as np# 读取图像 (以灰度模式)
img = cv2.imread('source.jpg', cv2.IMREAD_GRAYSCALE)
img = cv2.resize(img, (720, 480))
cv2.imwrite('source.jpg', img)
# 使用 Sobel 算子计算梯度
sobelx = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=3) # 水平方向
sobely = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=3) # 垂直方向# 计算梯度幅值
sobel = np.sqrt(sobelx**2 + sobely**2)
sobel = np.uint8(sobel) # 转换为 8 位无符号整数# 显示结果
cv2.imshow('Original', img)
cv2.imshow('Sobel', sobel)
cv2.imwrite('sobel.jpg', sobel)
cv2.waitKey(0)
cv2.destroyAllWindows()

3.2 Roberts 算子

Roberts 算子是一种非常简单且古老的边缘检测算子。它的核心思想是利用局部差分来近似图像的梯度，从而检测图像中的边缘。Roberts 算子使用两个 2x2 的卷积核，分别计算图像在对角线方向上的梯度。这两个卷积核如下：

Gx:
[1  0;0 -1]
Gy:
[0  1;-1 0]

卷积: 将图像分别与 Gx 和 Gy 卷积核进行卷积运算。卷积运算的目的是计算图像中每个 2x2 区域在对角线方向上的梯度值。
梯度幅值: 计算每个像素点的梯度幅值 (Magnitude)。梯度幅值表示该像素点处亮度变化的强度。

Roberts算子的特点:

计算简单: Roberts 算子的计算过程非常简单，只需要几个加减运算即可。
对噪声非常敏感: 由于 Roberts 算子只使用了 2x2 的卷积核，它对噪声非常敏感。图像中的任何微小噪声都可能导致梯度值的剧烈变化，从而被误认为是边缘。
定位精度较高: 由于 Roberts 算子使用了较小的卷积核，因此其边缘定位精度相对较高。
无法检测水平和垂直方向的边缘: Roberts 算子只能检测对角线方向的边缘，无法检测水平和垂直方向的边缘。
不常用: 由于其对噪声过于敏感，且无法检测所有方向的边缘，因此在实际应用中，Roberts 算子并不常用。通常会选择更鲁棒的边缘检测算子，例如 Sobel 算子或 Canny 算法。

import numpy as np
import cv2def roberts(img):"""使用 Roberts 算子进行边缘检测。Args:img: 输入图像 (灰度图像).Returns:边缘检测后的图像."""# Roberts 算子卷积核kernelx = np.array([[1, 0], [0, -1]])kernely = np.array([[0, 1], [-1, 0]])# 获取图像尺寸height, width = img.shape# 创建输出图像roberts_img = np.zeros((height, width), dtype=np.uint8)# 遍历图像像素for x in range(height - 1):for y in range(width - 1):# 提取 2x2 区域block = img[x:x+2, y:y+2]# 计算梯度gx = np.sum(block * kernelx)gy = np.sum(block * kernely)# 计算梯度幅值magnitude = np.sqrt(gx**2 + gy**2)# 将梯度幅值赋值给输出图像roberts_img[x, y] = magnitudereturn roberts_img# 读取图像 (以灰度模式)
img = cv2.imread('imgs/source.jpg', cv2.IMREAD_GRAYSCALE)# 应用 Roberts 算子
roberts_img = roberts(img)# 显示结果
cv2.imshow('Original', img)
cv2.imshow('Roberts', roberts_img)
cv2.destroyAllWindows()
cv2.imwrite('imgs/roberts.jpg', roberts_img)

Roberts 算子只适用于以下情况：

图像噪声非常小: 如果图像噪声非常小，可以使用 Roberts 算子进行简单的边缘检测。
对计算速度要求极高: 如果对计算速度要求极高，且可以容忍一定的误差，可以使用 Roberts 算子。
需要检测对角线方向的边缘: 如果只需要检测对角线方向的边缘，可以使用 Roberts 算子。

3.3 Prewitt 算子

Prewitt 算子是一种用于图像边缘检测的离散微分算子。它和 Sobel 算子类似，都是通过计算图像在水平和垂直方向上的梯度来检测边缘。但是，Prewitt 算子使用的卷积核与 Sobel 算子略有不同。Prewitt 算子使用两个 3x3 的卷积核，分别用于计算水平方向 (Gx) 和垂直方向 (Gy) 的梯度。这两个卷积核如下：

Gx:
[-1 0 1;-1 0 1;-1 0 1]
Gy:
[-1 -1 -1;0  0  0;1  1  1]

Prewitt算子特点:

简单易实现: Prewitt 算子的计算过程相对简单，容易在各种图像处理平台上实现。
对噪声敏感: Prewitt 算子对噪声比较敏感。在处理噪声较大的图像时，通常需要先进行平滑处理，例如使用高斯滤波器。
能够检测水平和垂直方向的边缘: Prewitt 算子能够同时检测图像中水平和垂直方向的边缘。
计算量相对较小: 相对于其他一些更复杂的边缘检测算法，Prewitt 算子的计算量较小，适合对实时性要求较高的应用。
权重相同: Prewitt 算子在计算梯度时，对中心像素周围的上下或左右像素赋予了相同的权重。这与 Sobel 算子不同，Sobel 算子对更靠近中心像素的像素赋予了更高的权重。
与 Sobel 算子的比较:Prewitt 算子和 Sobel 算子都是常用的梯度算子，它们的主要区别在于卷积核的权重分配不同。
Sobel 算子: 对中心像素周围的像素赋予了不同的权重，更靠近中心像素的权重更高。这种权重分配使得 Sobel 算子对噪声的抑制能力更强。
Prewitt 算子: 对中心像素周围的像素赋予了相同的权重。
一般来说，Sobel 算子的效果比 Prewitt 算子略好，因为 Sobel 算子考虑了像素距离的影响，对噪声的抑制能力更强。

import cv2
import numpy as npdef prewitt(img):"""使用 Prewitt 算子进行边缘检测。Args:img: 输入图像 (灰度图像).Returns:边缘检测后的图像."""# Prewitt 算子卷积核kernelx = np.array([[-1, 0, 1], [-1, 0, 1], [-1, 0, 1]])kernely = np.array([[-1, -1, -1], [0, 0, 0], [1, 1, 1]])# 使用 filter2D 函数进行卷积prewittx = cv2.filter2D(img, cv2.CV_64F, kernelx)prewitty = cv2.filter2D(img, cv2.CV_64F, kernely)# 计算梯度幅值prewitt = np.sqrt(prewittx**2 + prewitty**2)prewitt = np.uint8(prewitt)return prewitt# 读取图像 (以灰度模式)
img = cv2.imread('imgs/source.jpg', cv2.IMREAD_GRAYSCALE)# 应用 Prewitt 算子
prewitt_img = prewitt(img)# 显示结果
cv2.imshow('Original', img)
cv2.imshow('Prewitt', prewitt_img)
cv2.destroyAllWindows()
cv2.imwrite('imgs/prewitt.jpg', prewitt_img)

Prewitt 算子适用于以下情况：

需要快速进行边缘检测: Prewitt 算子的计算量较小，适合对实时性要求较高的应用。
图像噪声较小: 如果图像噪声较小，可以使用 Prewitt 算子进行边缘检测。
对边缘检测精度要求不高: 如果对边缘检测精度要求不高，可以使用 Prewitt 算子。

3.4 拉普拉斯算子

普拉斯算子计算的是图像的二阶导数，这使得它对图像中的细节更加敏感。拉普拉斯算子计算的是图像的标量场的散度（divergence）的梯度（gradient）。在二维图像中，拉普拉斯算子可以表示为：
$\nabla^{2} f = \partial^{2} f / \partial x^{2} + \partial^{2} f / \partial y^{2}$
其中, $\nabla^{2}$ 是拉普拉斯算子的符号。 $f (x, y)$ 是图像在 $(x, y)$ 处的像素值。 $\partial^{2} f / \partial x^{2}$ 是 $f (x, y)$ 对 $x$ 的二阶偏导数。 $\partial^{2} f / \partial y^{2}$ 是 $f (x, y)$ 对 $y$ 的二阶偏导数。在离散图像中，拉普拉斯算子可以使用卷积核来近似。常用的拉普拉斯算子卷积核如下：

标准形式:

[0  1  0;1 -4  1;0  1  0]

对角线形式:

[1  1  1;1 -8  1;1  1  1]

拉普拉斯算子的特点:

各向同性: 拉普拉斯算子是各向同性算子，即对图像旋转不敏感。无论图像如何旋转，拉普拉斯算子都能检测到相同的边缘。
对噪声敏感: 拉普拉斯算子对噪声非常敏感。由于拉普拉斯算子计算的是二阶导数，噪声会被放大，导致检测到大量的假边缘。
容易检测到双边缘: 拉普拉斯算子容易检测到双边缘。这是因为在边缘两侧，拉普拉斯值会发生剧烈的变化，从而产生两个零交叉点。
无法检测边缘方向: 拉普拉斯算子只能检测边缘的位置，无法检测边缘的方向。
常用于与其他方法结合使用: 由于拉普拉斯算子对噪声敏感，且容易检测到双边缘，因此在实际应用中，通常会与其他方法结合使用，例如先进行高斯滤波。

import cv2
import numpy as np# 读取图像 (以灰度模式)
img = cv2.imread('imgs/source.jpg', cv2.IMREAD_GRAYSCALE)# 应用拉普拉斯算子
laplacian = cv2.Laplacian(img, cv2.CV_64F)# 将结果转换为 8 位无符号整数 (取绝对值)
laplacian = np.uint8(np.abs(laplacian))# 显示结果
cv2.imshow('Original', img)
cv2.imshow('Laplacian', laplacian)
cv2.destroyAllWindows()
cv2.imwrite('imgs/lap.jpg', laplacian)

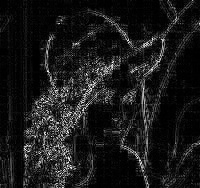
拉普拉斯算子适用于以下情况：

需要检测各向同性的边缘: 如果需要检测各向同性的边缘，可以使用拉普拉斯算子。
需要增强图像的细节: 拉普拉斯算子可以增强图像的细节，使其更加清晰。
与其他方法结合使用: 拉普拉斯算子通常会与其他方法结合使用，例如先进行高斯滤波，然后再使用拉普拉斯算子进行边缘检测。

3.5 LoG (Laplacian of Gaussian) 算子

由于拉普拉斯算子对噪声敏感，因此通常会先使用高斯滤波器对图像进行平滑处理，然后再使用拉普拉斯算子进行边缘检测。这种方法称为 LoG (Laplacian of Gaussian) 算子。

import cv2
import numpy as np# 读取图像 (以灰度模式)
img = cv2.imread('imgs/source.jpg', cv2.IMREAD_GRAYSCALE)# 高斯滤波
gaussian = cv2.GaussianBlur(img, (5, 5), 0)# 应用拉普拉斯算子
laplacian = cv2.Laplacian(gaussian, cv2.CV_64F)# 将结果转换为 8 位无符号整数 (取绝对值)
laplacian = np.uint8(np.abs(laplacian))# 显示结果
cv2.imshow('Original', img)
cv2.imshow('LoG', laplacian)
cv2.destroyAllWindows()
cv2.imwrite('imgs/log.jpg', laplacian)

3.6 DoG (Difference of Gaussians) 算子

DoG (Difference of Gaussians) 算子的核心思想是用两个不同方差（标准差）的高斯模糊图像的差分来逼近 LoG (Laplacian of Gaussian) 算子。由于 DoG 算子在计算上比 LoG 算子更有效率，因此在许多应用中被广泛使用。DoG 算子的数学表达式如下：
$Do G (x, y, σ 1, σ 2) = G (x, y, σ 1) - G (x, y, σ 2)$

其中， $Do G (x, y, σ 1, σ 2)$ 是DoG算子在 $(x, y) $处的输出值。$ G(x, y, σ)$是高斯模糊函数，定义为：
$G (x, y, σ) = (1/ (2 π σ^{2})) * e x p (- (x^{2} + y^{2}) / (2 σ^{2}))$

$σ 1$ 和 $σ 2$ 是两个不同方差（标准差）的高斯模糊函数的参数。通常， $σ 2$ > $σ 1$ 。DoG 算子可以用来近似 LoG 算子。理论证明，当 $σ 2 = kσ 1$ ，且 k 接近于 1 时，DoG 算子可以很好地逼近 LoG 算子：
$Do G \approx (k - 1) σ^{2} \nabla^{2} G$
其中， $\nabla^{2} G$ 是 LoG 算子。计算过程:

高斯模糊: 使用两个不同方差（σ1 和 σ2）的高斯滤波器对图像进行模糊处理，得到两个模糊图像。
差分: 将两个模糊图像相减，得到 DoG 图像。
零交叉点检测 (可选): 可以通过检测 DoG 图像中的零交叉点来确定边缘的位置。

DoG算子的特点:

计算效率高: DoG 算子的计算效率比 LoG 算子更高。这是因为 DoG 算子只需要进行两次高斯模糊和一次减法运算，而 LoG 算子需要计算二阶导数。
尺度空间分析: DoG 算子可以用于尺度空间分析。通过改变高斯滤波器的方差，可以检测到不同尺度的特征。
边缘检测: DoG 算子可以用于边缘检测。 DoG 图像中的零交叉点对应于图像中的边缘。

import cv2
import numpy as npdef dog(img, sigma1, sigma2):"""使用 DoG 算子进行图像增强和边缘检测。Args:img: 输入图像 (灰度图像).sigma1: 第一个高斯滤波器的标准差.sigma2: 第二个高斯滤波器的标准差.Returns:DoG 图像."""# 高斯模糊gaussian1 = cv2.GaussianBlur(img, (0, 0), sigma1)gaussian2 = cv2.GaussianBlur(img, (0, 0), sigma2)# 差分dog_img = gaussian1 - gaussian2return dog_img# 读取图像 (以灰度模式)
img = cv2.imread('imgs/source.jpg', cv2.IMREAD_GRAYSCALE)# 应用 DoG 算子
dog_img = dog(img, 1, 2)# 显示结果
cv2.imshow('Original', img)
cv2.imshow('DoG', dog_img)
cv2.imwrite('imgs/dog.jpg', dog_img)
cv2.destroyAllWindows()

DoG 算子适用于以下情况：

需要快速进行边缘检测: DoG 算子的计算效率高，适合对实时性要求较高的应用。
需要进行尺度空间分析: DoG 算子可以用于尺度空间分析，检测不同尺度的特征。
需要近似 LoG 算子: DoG 算子可以很好地逼近 LoG 算子。

3.7 Canny算子

Canny 算子是一种被广泛认为是最优的边缘检测算法之一。它由 John Canny 在 1986 年开发，旨在提供清晰、准确的边缘检测结果。 Canny 算子不仅能检测到图像中真实的边缘，还能最大限度地减少噪声的影响，并提供精确的边缘定位。
Canny 边缘检测算法是一个多步骤的过程，主要包括以下几个步骤：

高斯滤波 (Gaussian Filter):
- 目的: 降低图像噪声的影响。噪声会影响边缘检测的准确性，因此首先需要对图像进行平滑处理。
- 方法: 使用高斯滤波器对图像进行卷积。高斯滤波器是一种线性平滑滤波器，它可以有效地抑制高频噪声。
- 参数: 高斯滤波器的标准差 (σ) 是一个重要的参数，它决定了滤波器的平滑程度。较大的 σ 值会导致更强的平滑效果，但也可能模糊图像中的细节。
计算梯度幅值和方向 (Gradient Calculation):
- 目的: 检测图像中的边缘。边缘通常对应于图像中亮度变化剧烈的地方，即梯度较大的地方。
- 方法: 使用 Sobel 算子或其他梯度算子计算图像在水平和垂直方向上的梯度 (Gx 和 Gy)。然后，计算梯度幅值 (G) 和方向 (θ)：
  - 梯度幅值: G = sqrt(Gx^2 + Gy^2)
  - 梯度方向: θ = arctan(Gy / Gx)
  - 梯度方向量化: 将梯度方向量化为四个方向之一：0°, 45°, 90°, 135°。这是为了方便后续的非极大值抑制。
非极大值抑制 (Non-Maximum Suppression - NMS):
- 目的: 细化边缘，消除梯度方向上的非最大值，只保留最强的边缘像素。
- 方法: 遍历图像中的每个像素，如果该像素的梯度幅值在其梯度方向上不是局部最大值，则将其梯度幅值设置为 0。
- 步骤:
  - 对于每个像素，比较其梯度幅值与其梯度方向上的两个相邻像素的梯度幅值。
  - 如果该像素的梯度幅值不是局部最大值，则将其梯度幅值设置为 0。
双阈值处理 (Double Threshold):
- 目的: 将像素分为三类：强边缘像素、弱边缘像素和非边缘像素。
- 方法: 使用两个阈值：高阈值 (highThreshold) 和低阈值 (lowThreshold)。
  - 如果像素的梯度幅值大于高阈值，则将其标记为强边缘像素。
  - 如果像素的梯度幅值小于低阈值，则将其标记为非边缘像素。
  - 如果像素的梯度幅值介于高阈值和低阈值之间，则将其标记为弱边缘像素。
边缘连接 (Edge Tracking by Hysteresis):
- 目的: 连接弱边缘像素，形成完整的边缘。
- 方法: 遍历图像中的每个弱边缘像素。如果该弱边缘像素的周围 8 个像素中存在强边缘像素，则将其标记为边缘像素。否则，将其标记为非边缘像素。
- 滞后阈值处理: 这种边缘连接方法称为滞后阈值处理，它可以有效地连接边缘，并减少噪声的影响。

Canny 算子的特点包括：

优秀的边缘检测效果: Canny 算子能够检测到清晰、准确的边缘。
抗噪能力强: Canny 算子首先使用高斯滤波器降低噪声，然后使用非极大值抑制和双阈值处理进一步抑制噪声。
精确的边缘定位: Canny 算子使用非极大值抑制细化边缘，从而提供精确的边缘定位。
可调节的参数: Canny 算子有多个可调节的参数，例如高斯滤波器的标准差、高阈值和低阈值。可以根据具体的应用场景调整这些参数，以获得最佳的边缘检测效果。
计算复杂度较高: Canny 算子的计算复杂度相对较高，但由于其优秀的边缘检测效果，仍然被广泛应用于各种图像处理和计算机视觉应用中。

import cv2
import numpy as np# 读取图像 (以灰度模式)
img = cv2.imread('imgs/source.jpg', cv2.IMREAD_GRAYSCALE)# 应用 Canny 算子
edges = cv2.Canny(img, 100, 200)# 显示结果
cv2.imshow('Original', img)
cv2.imshow('Canny', edges)
cv2.destroyAllWindows()
cv2.imwrite('imgs/canny.jpg', edges)

Canny 算子适用于各种需要高质量边缘检测的场景，例如：

图像分割: 通过检测图像中的边缘，可以将图像分割成不同的区域。
目标检测: 边缘可以作为图像的特征，用于目标检测。
图像识别: 边缘可以作为图像的特征，用于图像识别。
医学图像分析: Canny 算子可以用于医学图像的边缘检测，例如肿瘤的边缘检测。
自动驾驶: Canny 算子可以用于自动驾驶系统中，检测道路和车辆的边缘。

3.8 罗盘算子

罗盘算子 (Compass Operator)通过使用一组预定义的卷积核来检测特定方向上的边缘。与 Sobel 或 Prewitt 等算子不同，罗盘算子不是简单地计算水平和垂直梯度，而是计算多个方向上的梯度响应，从而能够更精确地检测具有特定方向的边缘。罗盘算子的核心思想是使用一组卷积核，每个卷积核对应一个特定的方向（例如，北、东北、东、东南等）。将图像与每个卷积核进行卷积，得到该方向上的梯度响应。然后，选择具有最大梯度响应的方向作为该像素点的边缘方向。

常见的罗盘算子:

Kirsch 算子: 使用 8 个卷积核，分别对应 8 个方向（0°, 45°, 90°, 135°, 180°, 225°, 270°, 315°）。
Robinson 算子: 类似于 Kirsch 算子，也使用 8 个卷积核，但卷积核的系数略有不同。

Kirsch 算子使用 8 个 3x3 的卷积核，每个卷积核对应一个方向。这些卷积核如下：

N (北):
[-3 -3  5;-3  0  5;-3 -3  5]NE (东北):
[-3  5  5;-3  0  5;-3 -3 -3]E (东):
[ 5  5  5;-3  0 -3;-3 -3 -3]SE (东南):
[ 5  5 -3;5  0 -3;-3 -3 -3]S (南):
[ 5 -3 -3;5  0 -3;5 -3 -3]SW (西南):
[-3 -3 -3;5  0 -3;5  5 -3]W (西):
[-3 -3 -3;-3  0  5;-3  5  5]NW (西北):
[-3 -3 -3;-3  0 -3;5  5  5]

计算过程:

卷积: 将图像与每个卷积核进行卷积运算，得到 8 个方向上的梯度响应。
最大响应: 对于每个像素点，选择 8 个梯度响应中的最大值作为该像素点的梯度幅值。
边缘方向: 记录具有最大梯度响应的卷积核对应的方向作为该像素点的边缘方向。

罗盘算子的特点:

能够检测特定方向的边缘: 罗盘算子能够检测具有特定方向的边缘，这使得它在某些应用中比其他边缘检测算子更有效。
对噪声敏感: 类似于其他梯度算子，罗盘算子也对噪声比较敏感。
计算量较大: 由于需要进行多次卷积运算，罗盘算子的计算量相对较大。

import cv2
import numpy as npdef kirsch(img):"""使用 Kirsch 算子进行边缘检测。Args:img: 输入图像 (灰度图像).Returns:边缘检测后的图像和边缘方向图像."""# Kirsch 算子卷积核kernels = [np.array([[-3, -3, 5], [-3, 0, 5], [-3, -3, 5]]),  # Nnp.array([[-3, 5, 5], [-3, 0, 5], [-3, -3, -3]]),  # NEnp.array([[5, 5, 5], [-3, 0, -3], [-3, -3, -3]]),  # Enp.array([[5, 5, -3], [5, 0, -3], [-3, -3, -3]]),  # SEnp.array([[5, -3, -3], [5, 0, -3], [5, -3, -3]]),  # Snp.array([[-3, -3, -3], [5, 0, -3], [5, 5, -3]]),  # SWnp.array([[-3, -3, -3], [-3, 0, 5], [-3, 5, 5]]),  # Wnp.array([[-3, -3, -3], [-3, 0, -3], [5, 5, 5]])   # NW]# 获取图像尺寸height, width = img.shape# 创建输出图像magnitude = np.zeros((height, width), dtype=np.uint8)direction = np.zeros((height, width), dtype=np.uint8)# 遍历图像像素for x in range(1, height - 1):for y in range(1, width - 1):# 提取 3x3 区域block = img[x-1:x+2, y-1:y+2]# 计算每个方向上的梯度响应responses = [np.sum(block * kernel) for kernel in kernels]# 找到最大响应和对应的方向max_response = np.max(responses)max_index = np.argmax(responses)# 赋值给输出图像magnitude[x, y] = max_responsedirection[x, y] = max_index * 45  # 将索引转换为角度return magnitude, direction# 读取图像 (以灰度模式)
img = cv2.imread('imgs/source.jpg', cv2.IMREAD_GRAYSCALE)# 应用 Kirsch 算子
magnitude, direction = kirsch(img)# 显示结果
cv2.imshow('Original', img)
cv2.imshow('Kirsch Magnitude', magnitude)
cv2.imshow('Kirsch Direction', direction)
cv2.imwrite('imgs/kirsch_magnitude.jpg', magnitude)
cv2.destroyAllWindows()

罗盘算子适用于以下情况：

需要检测特定方向的边缘: 例如，在检测建筑物或道路的边缘时，可以使用罗盘算子来检测特定方向的直线。
需要获取边缘方向信息: 罗盘算子可以提供边缘的方向信息，这对于某些应用非常有用。

4 深度学习边缘检测

除了传统的边缘检测算子，深度学习也可以用于边缘检测。深度学习方法通常使用卷积神经网络 (CNN) 来学习图像中的边缘特征。这些 CNN 可以通过大量的训练数据来学习图像中的边缘特征。然后，这些 CNN 可以用于边缘检测。相较于传统的基于梯度或手工设计的算子，深度学习方法能够学习更复杂的图像特征，从而实现更准确、更鲁棒的边缘检测。

深度学习边缘检测的步骤:

数据准备: 收集大量的图像数据，并将其标记为边缘或非边缘。
模型训练: 使用 CNN 来训练模型。通常，CNN 由多个卷积层、池化层和全连接层组成。这些层可以学习图像中的边缘特征。
边缘检测: 使用训练好的模型来检测图像中的边缘。

深度学习边缘检测的优点:

能够学习更复杂的图像特征: 深度学习方法可以学习更复杂的图像特征，从而实现更准确的边缘检测。
能够处理复杂的图像: 深度学习方法可以处理复杂的图像，例如具有复杂背景的图像。

深度学习边缘检测的缺点:

计算量较大: 深度学习方法需要大量的计算资源，尤其是在处理大规模图像时。
训练数据量较大: 深度学习方法需要大量的训练数据，这需要大量的时间和计算资源。

深度学习边缘检测算法比较多，常见的有U-Net，Faster R-CNN，YOLO等。这里只简单较少其中的HED。HED 的核心思想是利用深度卷积神经网络学习图像的多尺度特征表示，并在网络的多个层次上进行边缘预测。通过将这些不同尺度的预测结果融合起来，HED 能够有效地利用图像的上下文信息，从而提高边缘检测的准确性。HED 的网络结构基于 VGG16 网络，并进行了一些修改，使其更适合边缘检测任务。主要的修改包括：在 VGG16 网络的每个卷积块 (convolutional block) 之后添加一个侧边输出 (side output)。每个侧边输出都连接到一个卷积层，用于预测该尺度下的边缘图。将所有侧边输出的预测结果融合起来，得到最终的边缘图。
HED 使用加权交叉熵损失函数 (weighted cross-entropy loss) 来训练网络。加权交叉熵损失函数可以有效地解决类别不平衡问题，即边缘像素数量远小于非边缘像素数量。损失函数定义如下：
$Loss = Σ (β * y_i * log(p_i) + (1 - β) * (1 - y_i) * log(1 - p_i))$
其中：

$y_i$ 是像素 i 的真实标签 (0 或 1)。
$p_i$ 是网络预测的像素 i 为边缘的概率。
$β$ 是一个权重，用于平衡边缘像素和非边缘像素的损失。通常，β 设置为边缘像素数量与非边缘像素数量的比值。
HED 的总损失函数是所有侧边输出层损失函数和融合层损失函数的加权和：
$Total Loss = Σ w_m * Loss_m + w_fuse * Loss_fuse$
其中：
$Loss_m$ 是第 m 个侧边输出层的损失函数。
$Loss_fuse$ 是融合层的损失函数。
$w_m$ 和 $w_fuse$ 是权重，用于平衡不同层次的损失。

5 参考文献

边缘检测
HED
Github-HED
基于深度学习的图像边缘和轮廓提取方法介绍