当前位置：首页 > news >正文

VTK编程指南＜五＞：VTK中的坐标系统、空间变换及VTK矩阵详解

news 来源：原创 2025/7/13 0:00:26

1、坐标系统

计算机图形学里常用的坐标系统主要有 4 种，分别是 Model 坐标系统、World 坐标系统、View坐标系统和 Display坐标系统(这些名词在不同的书里的中文表述均有所差别，所以直接使用英文名词表示)，此外还有两种表示坐标点的方式：以屏幕像素值为单位和归一化坐标值(各坐标轴取值范围为[-1,1])。它们之间的关系如图所示。

Model 坐标系统是定义模型时所采用的坐标系统，通常是局部的笛卡儿坐标系。

World坐标系统是放置Actor 的三维空间坐标系，Actor(vtkActor 类)其中的一个功能就是负责将模型从 Model 坐标系统变换到 World 坐标系统。每一个模型可以定义自己的 Model坐标系统，但World 坐标系只有一个，每一个Actor 必须通过放缩、旋转、平移等操作将 Model坐标系统转换到World 坐标系。World 坐标系同时也是灯光和相机所在的坐标系统。
在这里插入图片描述
View 坐标系统表示的是相机所看见的坐标系统。X、Y、Z 轴取值为[-1,1]，X、Y 值表示像平面上的位置，Z 值表示到相机的距离。相机负责将 World 坐标系变换到 View 坐标系。

Display 坐标系统与 View 坐标系统类似，但是各坐标轴的取值不是[-1,1]，而是使用屏幕像素值。屏幕上显示的不同窗口的大小会影响 View 坐标系的坐标值[-1，1]到 Display 坐标系的映射。可以把不同的渲染场景放在同一个窗口进行显示，例如，在一个窗口里，分为左右两个渲染场景，这左右的渲染场景(vtkRenderer)就是不同的视口(Viewport)。

示例 Viewport实现将一个窗口分为 4个视口,用vtkRenderer::SetViewport()来设置视口的范围(取值为[0,1])：

renderer1->SetViewport(0.0,0.0,0.5,0.5);
renderer2->SetViewport(0.5,0.0,1.0,0.5);
renderer3->SetViewport(0.0,0.5,0.5,1.0);
renderer4->SetViewport(0.5,0.5,1.0,1.0);

在VTK里，Model坐标系统用得比较少，其他三种坐标系统经常使用。它们之间的变换则是由类 vtkCoordinate 进行管理的。根据坐标值的单位、取值范围等不同，可以将坐标系统细分为如下几类。

DISPLAY——X、Y轴的坐标取值为渲染窗口的像素值。坐标原点位于渲染窗口的左下角，这个对于VTK里的所有二维坐标系统都是一样的，且VTK里的坐标系统都是采用右手坐标系。
NORMALIZED DISPLAY——X、Y 轴坐标取值范围为[0,1]，跟 DISPLAY一样，也是定义在渲染窗口里的。
VIEWPORT——X、Y的坐标值定义在视口或者渲染器(Renderer)里。
NORMALIZED VIEWPORT——X、Y 坐标值定义在视口或渲染器里，取值范围为[0,1]。
VIEW ——X、Y、Z 坐标值定义在相机所在的坐标系统里，取值范围为[-1，1]，Z值表示深度信息。
WORLD——X、Y、Z坐标值定义在世界坐标系统。
USERDEFINED——用户自定义坐标系统。

vtkCoordinate 可以用来表示坐标系统，其内部提供了函数接口来定义坐标系统:

SetCoordinateSystemToDisplay )
SetCoordinateSystemToNormalizedDisplay ()
SetCoordinateSystemToViewport ()
SetCoordinateSystemToNormalizedViewport )
SetCoordinateSystemToView O
SetCoordinateSystemToWorld ()

另外，该类还实现这些坐标系统之间的转换，例如下述代码实现了归一化窗口坐标与窗口坐标之间的转换:

vtkSmartPointer<vtkCoordinate>coordinate =
vtkSmartPointer<vtkCoordinate>::New);
coordinate->SetCoordinateSystemToNormalizedDisplay();
coordinate->SetValue(.5,.5,0);int*val;
val =coordinate_>GetComputedDisplay Value(renderer);

这里先调用了SetCoordinateSystemToNormalizedDisplay()设置坐标系统为归一化窗口坐标，并设置坐标值为(0.5,0.5,0)，即屏幕的中心;然后通过函数 GetComputedDisplayValue()实现窗口坐标的转换。该类中坐标系统转换函数如下：

GetComputedWorldValue)
GetComputedViewportValue()
GetComputedDisplayValue)
GetComputedLocalDisplayValue()
GetComputedDoubleViewportValue()
GetComputedDoubleDisplayValue)
GetComputedUserDefinedValue()

2、空间变换

在三维空间里定义的三维模型，最后显示时都是投影到二维平面，比如在屏幕上显示。三维到二维的投影包括透视投影(Perspective Projection)和正交投影(Orthogonal Projection)。正交投影也叫平行投影。
在这里插入图片描述

VTK 里与空间变换相关的类有 vtkTransform2D，vtkTransform，vtkPerspectiveTransform，vtkGeneralTransform，vtkTransformFilter，vtkMatrix4 X 4 等。例如下面代码实现了vtkActor对象的空间变换：

vtkSmartPointer<vtkTransform>transform =
vtkSmartPointer<vtkTransform>::New);
transform->PostMultiply0;
transform->RotateZ(40);
transform->Translate(10,0,0);
cylinderActor->SetUserTransform(transform);

先定义了vtkTransform 对象，并设置使用右乘计算变换矩阵。RotateZ()设置绕 Z 轴旋转40°，并使用Translate()设置平移大小为(10,0,0)，最后通过 vtkActor::SetUserTransform()方法设置用户定义的变换矩阵，实现模型的空间变换。

3、矩阵

3.1、齐次坐标

常见的点一般是Pt（X,Y,Z），相当于一个1×3矩阵，而矩阵相乘的话一般是第一个矩阵的列数要等于第二个矩阵的行数。此处需要引入齐次坐标的概念：从广义上讲，齐次坐标就是用n+1维向量表示n 维向量，即将n维空间的点用 n+1维坐标表示。例如，一般笛卡尔坐标系中的二维点向量[x y]可用齐次坐标表示为[Hx Hx H]，其中最后一维坐标是一个标量，称为比例因子。利用齐次坐标可以将平移、旋转、比例、投影等几何变换统一到矩阵的乘法上来，为图形变换提供方便。

该矩阵在右手坐标系中定义，其中左上角部分产生比例、对称、错切和旋转变换，右上角部分产生平移变换;左下角部分产生透视变换;右下角部分产生全比例变换。
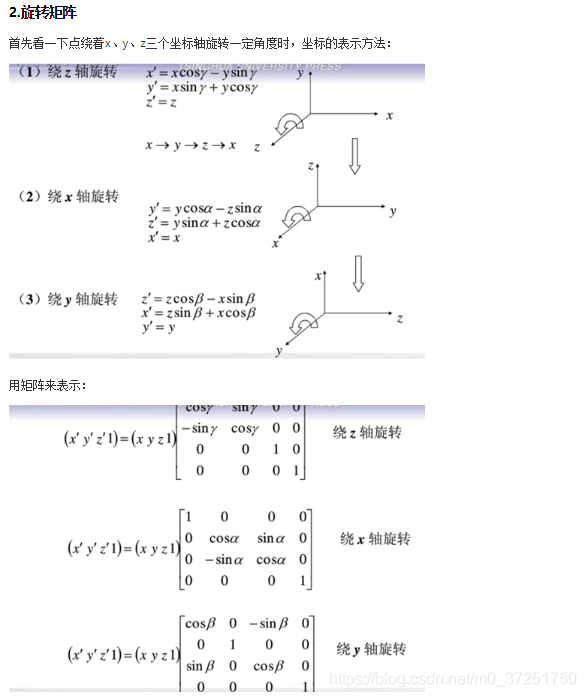
在这里插入图片描述

3.2、矩阵旋转

在这里插入图片描述
有兴趣可以将上述三个旋转矩阵按照不同的顺序进行相乘，得到的结果也是不一样的，例如：
1）先旋转x轴再旋转y轴再旋转z轴；
2）先旋转y轴再旋转x轴再旋转z轴；
3）先旋转z轴再旋转y轴再旋转x轴；

3.3、vtkMatrix4x4类

3.3.1 vtkMatrix4x4初始化

matrix1:
-0.013 -0.986 0.165 -133
-0.017 0.166 0.986 -35
-1 0.01 -0.02 40
0 0 0 1

	vtkMatrix4x4* matrix1 = vtkMatrix4x4::New();matrix1->Identity();matrix1->SetElement(0, 0, -0.013);matrix1->SetElement(0, 1, -0.986);matrix1->SetElement(0, 2, 0.165);matrix1->SetElement(0, 3, -133);matrix1->SetElement(1, 0, -0.017);matrix1->SetElement(1, 1, 0.166);matrix1->SetElement(1, 2, 0.986);matrix1->SetElement(1, 3, -35);matrix1->SetElement(2, 0, -1.0);matrix1->SetElement(2, 1, 0.01);matrix1->SetElement(2, 2, -0.02);matrix1->SetElement(2, 3, 40);

3.3.2 vtkMatrix4x4相乘

下面两个矩阵的结果是不一样的，也就是常说的矩阵乘法左乘和右乘不一样。

	vtkMatrix4x4::Multiply4x4(matrix1, matrix2, matrix3);vtkMatrix4x4::Multiply4x4(matrix2, matrix1, matrix4);

下面是完整的结果和代码：

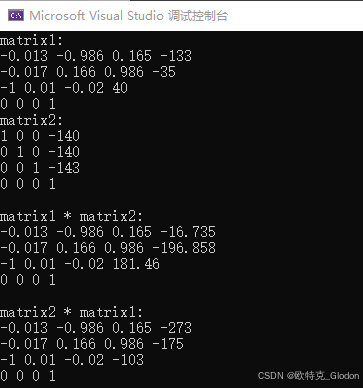
在这里插入图片描述

#include <iostream>
#include <vtkMatrix4x4.h>int main()
{vtkMatrix4x4* matrix1 = vtkMatrix4x4::New();matrix1->Identity();matrix1->SetElement(0, 0, -0.013);matrix1->SetElement(0, 1, -0.986);matrix1->SetElement(0, 2, 0.165);matrix1->SetElement(0, 3, -133);matrix1->SetElement(1, 0, -0.017);matrix1->SetElement(1, 1, 0.166);matrix1->SetElement(1, 2, 0.986);matrix1->SetElement(1, 3, -35);matrix1->SetElement(2, 0, -1.0);matrix1->SetElement(2, 1, 0.01);matrix1->SetElement(2, 2, -0.02);matrix1->SetElement(2, 3, 40);vtkMatrix4x4* matrix2 = vtkMatrix4x4::New();matrix2->Identity();matrix2->SetElement(0, 3, -140);matrix2->SetElement(1, 3, -140);matrix2->SetElement(2, 3, -143);vtkMatrix4x4* matrix3 = vtkMatrix4x4::New();matrix3->Identity();vtkMatrix4x4* matrix4 = vtkMatrix4x4::New();matrix4->Identity();vtkMatrix4x4::Multiply4x4(matrix1, matrix2, matrix3);vtkMatrix4x4::Multiply4x4(matrix2, matrix1, matrix4);// 打印结果矩阵以验证std::cout << "matrix1: " << std::endl;for (int i = 0; i < 4; ++i){for (int j = 0; j < 4; ++j){std::cout << matrix1->GetElement(i, j) << " ";}std::cout << std::endl;}std::cout << "matrix2: " << std::endl;for (int i = 0; i < 4; ++i){for (int j = 0; j < 4; ++j){std::cout << matrix2->GetElement(i, j) << " ";}std::cout << std::endl;}std::cout << std::endl;std::cout << "matrix1 * matrix2: " << std::endl;for (int i = 0; i < 4; ++i) {for (int j = 0; j < 4; ++j) {std::cout << matrix3->GetElement(i, j) << " ";}std::cout << std::endl;}std::cout << std::endl;std::cout << "matrix2 * matrix1: " << std::endl;for (int i = 0; i < 4; ++i){for (int j = 0; j < 4; ++j){std::cout << matrix4->GetElement(i, j) << " ";}std::cout << std::endl;}// 释放内存matrix1->Delete();matrix2->Delete();matrix3->Delete();matrix4->Delete();return 1;
}