【霍夫变换】图像处理(OpenCV)-part11
20 霍夫变换
20.1 理解霍夫变换
霍夫变换的基本思想是将图像空间中的几何元素(如直线、圆等)通过参数方程转换到参数空间中,形成一个参数空间的累加器数组。图像空间中的每个点在参数空间中对应一个曲线或曲面,而几何形状在图像空间中的对应关系则表现为参数空间中的曲线或曲面的交点。通过在参数空间中寻找累加器数组的局部极大值,可以确定这些几何形状的参数,从而实现对图像中相应形状的检测。
霍夫变换是图像处理的一种技术,主要用于检测图像中的直线、圆等几何形状。基本思想就是将图像空间中的点映射到参数空间中,通过在参数空间中寻找累计最大值实现对特定形状的检测。

20.2 霍夫直线变换
对于一条直线(不垂直于x轴的直线),都可以用y=k x+q来表示,此时,x和y是横纵坐标,k和q是一个固定参数。当我们换一种方式来看待这个式子,我们就可以得到:
q = -kx + y
此时,以k和q为横纵坐标,x和y为固定参数,也就是说k和q成了自变量和因变量,变换如下图所示:

从上图可以看出,在直角坐标系下的一个直线,在变换后的空间中仅仅表示为一点,对于变换后的空间,我们称其为霍夫空间,也就是参数空间。也就是说,直角坐标系下的一条直线对应了霍夫空间中的一个点。类似的,霍夫空间中的一条直线也对应了直角坐标系中的一个点,如下图所示:

那么对于一个二值化后的图形来说,其中的每一个目标像素点(这里假设目标像素点为白色像素点)都对应了霍夫空间的一条直线,当霍夫空间中有两条直线相交时,就代表了直角坐标系中某两个点所构成的直线。而当霍夫空间中有很多条线相交于一点时,说明直角坐标系中有很多点能构成一条直线,也就意味着这些点共线,因此我们就可以通过检测霍夫空间中有最多直线相交的交点来找到直角坐标系中的直线。
基本对应关系
直线与点:在直角坐标系中,直线 y=ax+b,参数空间用 a(斜率)和 b(截距)表示直线,所以直角坐标系的一条直线对应参数空间的一个点 (a,b)。
点与直线:在直角坐标系中,一个点 (x0,y0),代入直线方程得 y0=ax0+b,变形为 b=y0−ax0,这在参数空间是一条直线。参数空间的这条直线代表所有可能经过直角坐标系点 (x0,y0) 的直线的参数组合。
直角坐标系与霍夫空间的联系
两直线相交:直角坐标系中的两个点 (x1,y1) 和 (x2,y2),它们在参数空间分别对应直线 b=y1−ax1 和 b=y2−ax2。联立解方程,可得交点 (a′,b′)。此交点即所求直线的参数,对应直角坐标系中两点连成的直线方程 y=a′x+b′。
多线相交于一点:若有多个点共线,这些点在直角坐标系的直线方程为 y=a0x+b0。在参数空间,每个共线点对应的直线都经过 (a0,b0),多条直线交于一点,说明直角坐标系的多个点共线,参数空间交点即共线直线参数。
参数坐标系中,相交在一点的直线越多,说明在直角坐标系中,有越多的点构成直线
总结
参数空间中,相交在一点的直线越多,说明在直角坐标系中,有越多的点构成直线。
累加器值表示有多少个点共线。
通过寻找参数空间中累加器值的局部极大值,可以检测出直角坐标系中的直线。
然而对于x=1这种直线(垂直于x轴)来说,y已经不存在了,斜率无穷大,无法映射到霍夫空间中去,那么就没办法使用上面的方法进行检测了,为了解决这个问题,我们就将直角坐标系转化为极坐标系,然后通过极坐标系与霍夫空间进行相互转化。
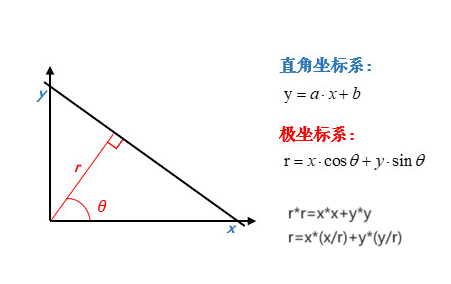
在极坐标系下是一样的,极坐标中的点对于霍夫空间中的线,霍夫空间中的点对应极坐标中的直线。并且此时的霍夫空间不再是以k为横轴、b为纵轴,而是以为θ横轴、ρ(上图中的r)为纵轴。上面的公式中,x、y是直线上某点的横纵坐标(直角坐标系下的横纵坐标),和是极坐标下的坐标,因此我们只要知道某点的x和y的坐标,就可以得到一个关于θ-ρ的表达式,如下图所示:

根据上图,霍夫空间在极坐标系下,一点可以产生一条三角函数曲线,而多条这样的曲线可能会相交于同一点。因此,我们可以通过设定一个阈值,来检测霍夫空间中的三角函数曲线相交的次数。如果一个交点的三角函数曲线相交次数超过阈值,那么这个交点所代表的直线就可能是我们寻找的目标直线。
使用API
lines=cv2.HoughLines(image, rho, theta, threshold)
image:输入图像,通常为二值图像,其中白点表示边缘点,黑点为背景。
rho:r的精度,以像素为单位,表示霍夫空间中每一步的距离增量, 值越大,考虑越多的线。
theta:角度θ的精度,通常以弧度为单位,表示霍夫空间中每一步的角度增量。值越小,考虑越多的线。
threshold:累加数阈值,只有累积投票数超过这个阈值的候选直线才会被返回。返回值:
cv2.HoughLines函数返回一个二维数组,每一行代表一条直线在霍夫空间中的参数(rho, theta)。
import cv2 as cv
import numpy as np
img = cv.imread("images/huofu.png")
#灰度转换
img_gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
#边缘检测
img_edge = cv.Canny(img_gray, 30, 70)
#霍夫直线变换
lines = cv.HoughLines(img_edge, 0.8, np.pi/180, 90)
for line in lines:rho,theta = line[0]sin_theta = np.sin(theta)cos_theta = np.cos(theta)x1,x2 = 0,img_edge.shape[1]y1,y2 = int((rho -x1 * cos_theta)/sin_theta),int((rho -x2 * cos_theta)/sin_theta)cv.line(img, (x1,y1), (x2,y2), (100,100,255), 1)
cv.imshow("img", img)
cv.waitKey()
cv.destroyAllWindows()
20.3 统计概率霍夫直线变换
前面的方法又称为标准霍夫变换,它会计算图像中的每一个点,计算量比较大,另外它得到的是整一条线(r和θ),并不知道原图中直线的端点。所以提出了统计概率霍夫直线变换(Probabilistic Hough Transform),是一种改进的霍夫变换,它在获取到直线之后,会检测原图中在该直线上的点,并获取到两侧的端点坐标,然后通过两个点的坐标来计算该直线的长度,通过直线长度与最短长度阈值的比较来决定该直线要不要被保留。
使用API
lines=cv2.HoughLinesP(image, rho, theta, threshold, lines=None, minLineLength=0, maxLineGap=0)
image:输入图像,通常为二值图像,其中白点表示边缘点,黑点为背景。
rho:极径分辨率,以像素为单位,表示极坐标系中的距离分辨率。
theta:极角分辨率,以弧度为单位,表示极坐标系中角度的分辨率。
threshold:阈值,用于过滤掉弱检测结果,只有累计投票数超过这个阈值的直线才会被返回。
lines(可选):一个可初始化的输出数组,用于存储检测到的直线参数。
minLineLength(可选):最短长度阈值,比这个长度短的线会被排除。
maxLineGap(可选):同一直线两点之间的最大距离。当霍夫变换检测到一系列接近直角的线段时,这些线段可能是同一直线的不同部分。maxLineGap参数指定了在考虑这些线段属于同一直线时,它们之间最大可接受的像素间隔。返回值lines:
cv2.HoughLinesP函数返回一个二维数组,每个元素是一个包含4个元素的数组,分别表示每条直线的起始点和结束点在图像中的坐标(x1, y1, x2, y2)。
def func2():# 读取图像img = cv.imread("images/huofu.png")if img is None:print("无法加载图像,请检查文件路径是否正确。")return# 灰度转换img_gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)# 边缘检测img_edge = cv.Canny(img_gray, 30, 70)# 霍夫直线变换lines = cv.HoughLinesP(img_edge, 1, np.pi/180, 100, minLineLength=100, maxLineGap=10)# 遍历所有检测到的直线for line in lines:x1, y1, x2, y2 = line[0]cv.line(img, (x1, y1), (x2, y2), (100, 200, 200), 2)# 显示结果cv.imshow("img", img)cv.waitKey()cv.destroyAllWindows()func2()
20.4 霍夫圆变换
霍夫圆变换跟直线变换类似,它可以从图像中找出潜在的圆形结构,并返回它们的中心坐标和半径。只不过线是用(r,θ)表示,圆是用(x_center,y_center,r)来表示,从二维变成了三维,数据量变大了很多;所以一般使用霍夫梯度法减少计算量。
使用API
circles=cv2.HoughCircles(image, method, dp, minDist, param1, param2)
image:输入图像,通常是灰度图像。
method:使用的霍夫变换方法:霍夫梯度法,可以是cv2.HOUGH_GRADIENT,这是唯一在OpenCV中用于圆检测的方法。
dp:累加器分辨率与输入图像分辨率之间的降采样比率,用于加速运算但不影响准确性。设置为1表示霍夫梯度法中累加器图像的分辨率与原图一致
minDist:检测到的圆心之间的最小允许距离,以像素为单位。在霍夫变换检测圆的过程中,可能会检测到许多潜在的圆心。minDist参数就是为了过滤掉过于接近的圆检测结果,避免检测结果过于密集。当你设置一个较小的minDist值时,算法会尝试找出尽可能多的圆,即使是彼此靠得很近的圆也可能都被检测出来。相反,当你设置一个较大的minDist值时,算法会倾向于只检测那些彼此间存在一定距离的独立的圆。
param1和param2:这两个参数是在使用cv2.HOUGH_GRADIENT方法时的特定参数,分别为:
param1(可选):阈值1,决定边缘强度的阈值。
param2:阈值2,控制圆心识别的精确度。较大的该值会使得检测更严格的圆。param2通常被称为圆心累积概率的阈值。在使用霍夫梯度方法时,param2设置的是累加器阈值,它决定了哪些候选圆点集合被认为是有效的圆。较高的param2值意味着对圆的检测更严格,只有在累加器中积累了足够高的响应值才认为是真实的圆;较低的param2值则会降低检测的门槛,可能会检测到更多潜在的圆,但也可能包含更多的误检结果。返回值:
cv2.HoughCircles返回一个二维numpy数组,包含了所有满足条件的圆的参数。
def func3():# 读取图像img = cv.imread("images/huofu.png")if img is None:print("无法加载图像,请检查文件路径是否正确。")return# 灰度转换img_gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)# 边缘检测img_edge= cv.Canny(img_gray, 30, 70)# 霍夫圆变换circles = cv.HoughCircles(img_edge, cv.HOUGH_GRADIENT, 1, 20, param1=50, param2=30, minRadius=0, maxRadius=0)if circles is not None:circles = np.uint16(np.around(circles))print(circles)for circle in circles[0, :]:x, y, r = circlecv.circle(img, (x, y), r, (100, 200, 255), 2)# 显示结果cv.imshow("img", img)cv.waitKey()cv.destroyAllWindows()func3()
相关文章:
-part11)
【霍夫变换】图像处理(OpenCV)-part11
20 霍夫变换 20.1 理解霍夫变换 霍夫变换的基本思想是将图像空间中的几何元素(如直线、圆等)通过参数方程转换到参数空间中,形成一个参数空间的累加器数组。图像空间中的每个点在参数空间中对应一个曲线或曲面,而几何形状在图像…...

Flink 源码编译
打包命令 打包整个项目 mvn clean package -DskipTests -Drat.skiptrue打包单个模块 mvn clean package -DskipTests -Drat.skiptrue -pl flink-dist如果该模块依赖其他模块,可能需要先将其他模块 install 到本地,如果依赖的模块的源代码有修改&#…...

React19源码阅读之commitRoot
commitRoot入口 在finishConcurrentRender函数,commitRootWhenReady函数,commitRoot函数。 commitRoot流程图 commitRoot函数 commitRoot 函数是 React 渲染流程中用于提交根节点的关键函数。它的主要作用是设置相关的优先级和状态,然后调…...

单 例 模 式
设计模式(Design Pattern)说白了就是一套方法论,是我们的前辈们不断试错总结出来的。一般意义上的设计模式有23种,分为创建型、结构型、行为型三大类。今天先拿最简单的单例模式开刀吧。 六大原则 在正式进入设计模式的学习之前&…...

如何在 Postman 中,自动获取 Token 并将其赋值到环境变量
在 Postman 中,你可以通过 预请求脚本(Pre-request Script) 和 测试脚本(Tests) 实现自动获取 Token 并将其赋值到环境变量,下面是完整的操作步骤: ✅ 一、创建获取 Token 的请求 通常这个请求…...

CentOS 7 基于 Nginx 的 HTML 部署全流程指南
一、Nginx 安装(两种主流方式) 1. YUM 安装(推荐新手) # 安装 EPEL 扩展源(部分系统需要) yum install epel-release -y# 安装 Nginx yum install nginx -y# 启动并设置开机自启 systemctl start nginx s…...

spring-ai使用Document存储至milvus的数据结构
1、 spring:application:name: spring-ai-alibaba-rag-milvus-exampleai:dashscope:api-key: sk-xxxxxxoooooovectorstore:milvus:client:host: xxx.ooo.mmm.nnnport: 19530username: rootpassword: MilvusdatabaseName: defaultcollectionName: vector_store#初始化 collecti…...
:Collection 管理分区、管理别名)
Milvus(6):Collection 管理分区、管理别名
1 管理分区 分区是一个 Collection 的子集。每个分区与其父集合共享相同的数据结构,但只包含集合中的一个数据子集。本页将帮助你了解如何管理分区。 1.1 分区概述 创建一个 Collection 时,Milvus 也会在该 Collection 中创建一个名为_default 的分区。…...

关于Safari浏览器在ios<16.3版本不支持正则表达式零宽断言的解决办法
异常原因 今天在升级Dify版本的时候发现低版本的ios手机出现了以下报错: SyntaxError: Invalid regular expression: invalid group specifier nameError: Invalid regular expression: invalid group specifier name Call Stack 46 eval [native code] (0:0) ./n…...

设计模式--建造者模式详解
建造者模式 建造者模式也属于创建型模式,它提供了一种创建对象的最佳方式 定义:将一个复杂对象的构建和它的表示分离,使得同样的构建过程可以创建不同的表示(假设有不同的建造者实现类,可以产生不同的产品)…...

玩转Docker | Docker部署LMS轻量级音乐工具
玩转Docker | Docker部署LMS轻量级音乐工具 前言一、LMS介绍LMS简介主要特点二、系统要求环境要求环境检查Docker版本检查检查操作系统版本三、部署LMS服务下载镜像创建容器创建容器检查容器状态检查服务端口安全设置四、访问LMS服务访问LMS首页注册账号五、基本使用上传音乐文…...

【前端】【业务场景】【面试】在前端项目中,当涉及大量数据渲染时,如何提高渲染性能并避免页面卡顿?
大量数据渲染性能优化:四层进阶法 循序渐进:先限量 → 再懒渲 → 后分批 → 终极后台协作 1 虚拟滚动:一次只保留“看得见”的节点 核心思路:固定容器高度,让滚动条滚动 假象 的总长度;可视窗口内…...

数据结构与算法实战:从理论到落地的深度探索
放在前面咯 数据结构与算法实战:从理论到落地的深度探索 数据结构与算法实战:从理论到落地的深度探索 在计算机科学的浩瀚宇宙中,数据结构与算法犹如璀璨星辰,指引着高效程序设计的方向。它们不仅是开发者解决复杂问题的核心利…...

大文件上传Demo及面试要点
大文件上传功能实现原理 - 面试解析 在面试中解释大文件上传功能的实现原理时,可以从以下几个方面进行说明: 1. 分片上传 (Chunked Upload) 实现原理 : 前端将大文件分割为固定大小(如5MB)的多个分片(Chunk)每个分片独立上传,…...

安宝特案例 | 物流仓储头部企业应用AR+作业流,规范日常安全点检,保障消防安全
安全点检管理的真实性缺失将会造成极大损失。 仓储物流行业有仓库面积大、货物堆放密集、包装材料易燃、整体货值高的特点,且造成火灾的隐患包括建筑结构隐患、消防设置失效、货物存放与操作隐患、电气系统问题、人为因素等,因此安全管理被放在重要位置…...

关于 xpath 查找 XML 元素的一点总结
测试环境 Win7 64 python 3.4.0 实践出真知 代码如下,更换不同的 xpath,和 response_to_check 进行测试 实验 1 xpath ".//xmlns:return//xmlns:copeWith" response_to_check \ <soap:Envelope xmlns"http://www.examp.com…...
)
JavaScript学习教程,从入门到精通,XMLHttpRequest 与 Ajax 请求详解(25)
XMLHttpRequest 与 Ajax 请求详解 一、XMLHttpRequest 概述 XMLHttpRequest (XHR) 是一个 JavaScript API,用于在浏览器和服务器之间传输数据,而无需刷新页面。它是实现 Ajax (Asynchronous JavaScript and XML) 技术的核心。 主要特点: …...

HTML、XHTML 和 XML区别
HTML、XHTML 和 XML 这三兄弟的区别 HTML: 老大哥,负责网页长啥样,性格比较随和,有点小错误也能容忍。XHTML: 二哥,看着像 HTML,但规矩严,是按 XML 的规矩来的 HTML,更规范。XML: 小弟…...

形象解释 HTTP 的四种常见请求方式及其中的区别联系
HTTP 的常见请求方式常见的有四种:GET、POST、PUT、DELETE,它们各自的功能不一样。 🍜 场景比喻:HTTP 请求像“去餐厅点菜” 请求方式行为餐厅比喻说明GET获取数据看菜单/问服务员:你们有什么菜?不带食材、…...

微信小程序根据图片生成背景颜色有效果图
效果图 取得是图片中间10个像素算出背景颜色 .wxml <canvas type"2d" id"imageCanvas" style"--w: {{w}}px;--h: {{h}}px;" /> <view style"background: {{backgroundColor}};"><image bind:tap"updateIndex&qu…...

实时步数统计系统 kafka + spark +redis
基于微服务架构设计并实现了一个实时步数统计系统,采用生产者-消费者模式,利用Kafka实现消息队列,Spark Streaming处理实时数据流,Redis提供高性能数据存储,实现了一个高并发、低延迟的数据处理系统,支持多…...

使用 Docker 安装 SQL Server 2022 并解决 Navicat 连接问题
在使用 Docker 安装 SQL Server 时,很多人可能遇到过无法通过 Navicat 等数据库客户端连接到容器的情况。尤其是尝试使用 mcr.microsoft.com/mssql/server:2022-latest 镜像时,可能会发现 Navicat一直转圈,无法连接到数据库。在这篇博客中&am…...

使用 Node、Express 和 MongoDB 构建一个项目工程
本文将详细介绍如何使用 Node.js Express MongoDB 构建一个完整的 RESTful API 后端项目,涵盖: 项目初始化 Express 服务器搭建 MongoDB 数据库连接 REST API 设计(CRUD 操作) 错误处理与中间件 源码结构与完整代码 部署建…...

基本元器件电阻、电容、电感的高频知识和大厂真题解析
本文首先举例分析各个方向的工程师如何定制化准备硬件岗位面试,各个击破; 然后根据实战经验总结硬件领域中电阻电容电感等的主要笔试、面试高频考题考点; 最后,列出最新最全的基本元器件笔试面试的真题和模拟题,供大家参考。 本专栏预计更新50期左右。当前第3期 一、硬件…...

Unity InputSystem触摸屏问题
最近把Unity打包后的windows软件放到windows触摸屏一体机上测试,发现部分屏幕触摸点击不了按钮,测试了其他应用程序都正常。 这个一体机是这样的,一个电脑机箱,外接一个可以触摸的显示屏,然后UGUI的按钮就间歇性点不了…...

分布式微服务架构,数据库连接池设计策略
在分布式微服务架构中,数据库连接池的设计远比单体应用复杂,涉及资源隔离、连接管理、性能调优和高可用等问题。下面是面向专业软件架构师的系统化分析与策略建议: 一、核心挑战 每个服务独立运行,连接池分散 每个微服务维护自己的…...

差分信号抗噪声原理:
差分信号抗噪声原理: 差分信号除了能很好地解决发送和接收参考点电位不同的问题外,差分信号的另一个重要优势就是在一定条件下其抗干扰能力比单端信号更强。对于单端信号传输,外界对它的干扰噪声直接叠加在信号上,接收端直接检测输…...

【数据分析】酵母实验多指标数据的 R 语言分析与可视化
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍加载必要的R包数据下载定义函数发育分析(development analysis)数据导入与预处理数据子集创建绘图模型分析两两比较生存分析(survival analysis)数据导入与预处理数据子集创建绘…...

AI | 最近比较火的几个生成式对话 AI
关注:CodingTechWork 引言 生成式对话 AI 正在迅速改变我们与机器交互的方式,从智能助手到内容创作,其应用范围广泛且深远。本文将深入探讨几款当前热门的生成式对话 AI 模型,包括 Kimi、DeepSeek、ChatGPT、文心一言、通义千问和…...

将视频生成视频二维码步骤
如何将视频链接生成二维码 生成与视频关联的二维码通常涉及以下几个方面:选择合适的库或工具、准备视频链接以及将其转换为二维码图像。以下是详细的说明: 使用JavaScript/Vue框架生成二维码 在前端开发中,可以使用 qrcode 或者 vue-qrcod…...

以安科瑞 EMS3.0 为依托,打造网荷储充一体化典范
在“双碳”目标与能源革命的浪潮中,安科瑞电气股份有限公司推出的EMS3.0微电网智慧能源平台,以“源-网-荷-储-充”全链路协同为核心,通过物联网、大数据与AI技术的深度融合,为企业提供了一套智能化、高效化、低碳化的能源管理解决…...
(C/C++))
堆和二叉树--数据结构初阶(3)(C/C++)
文章目录 前言理论部分堆的模拟实现:(这里举的大根堆)堆的创建二叉树的遍历二叉树的一些其他功能实现 作业部分 前言 这期的话讲解的是堆和二叉树的理论部分和习题部分 理论部分 二叉树的几个性质:1.对于任意一个二叉树,度为0的节点比度为2的节点多一个 2.对于完全…...
)
CLIP和SimCLR集成到图像-文本检索系统技术实现步骤和部署方案(代码版)
将 CLIP(多模态对比学习)和 SimCLR(单模态对比学习)集成到 图像-文本检索系统(如搜索引擎、电子商务平台)的技术实现步骤和部署方案,结合代码示例与工程化思路: ### 一、技术实现核心步骤 1. 环境搭建与依赖安装 # 安装 PyTorch(支持 GPU 加速) pip install torch…...

R/G-B/G色温坐标系下对横纵坐标取对数的优势
有些白平衡色温坐标系会分别对横纵坐标取对数运算。 这样做有什么优势呢? 我们知道对数函数对0-1之间的因变量值具有扩展作用。即自变量x变化比较小时,经过对数函数作用后可以把因变量扩展到较大范围内,即x变化较小时,y变化较大,增加了识别数据的识别性。 由于Raw数据中的…...

Java开发工具IntelliJ IDEA v2025.1——全面支持Java 24、整合AI
IntelliJ IDEA 是由 JetBrains 开发的智能 Java IDE,提供代码自动补全、重构工具、框架集成(Spring/JPA 等)、数据库工具和调试支持,通过深度代码分析与跨语言功能优化企业级开发流程,被广泛认可为专业 Java 开发者的高…...

IDEA启动报错Failed to create JVM. JVM path的解决办法
今天修改了 IntelliJ IDEA 2023.1 的配置文件 idea64.exe.vmoptions 后启动报错: if you already hava a JDK installed, define a JAVA_HOME variable in Computer > Systen Properties > System Settings > Environment Variables.Failed to create JV…...

R语言中的常用内置函数
常用的数值函数 常用的字符函数 与概率分布相关的函数 有用的统计函数 数据来源:《数据挖掘与数据分析:基于R语言》王阳 2024年1月出版...

docker容器监控自动恢复
关于实现对docker容器监控以及自动恢复,这里介绍两种实现方案。 方案1: 实现思路: 找到(根据正则表达式)所有待监控的docker容器,此处筛选逻辑根据docker运行状态找到已停止(Exit)类…...

【记录手贱bug日常】IDEA 配置vmoptions后打不开,重新安装,删注册表均无用
今天早上来公司,闲着没事优化优化自己的"锄头"idea,然后想着看看idea用的啥垃圾回收器,后来手动改成了-XX:UseG1GC,满心欢喜觉得没什么问题,直接删除缓存重启,结果不出意料的出问题了,…...
)
STM32F407使用ESP8266实现阿里云OTA(中)
文章目录 前言一、程序分析二、程序讲解1. main函数2. Get_Version()函数3. esp_Init()函数4. Check_Updata()函数结语前言 从上一章STM32F407使用ESP8266实现阿里云OTA(上)中我们已经对连接阿里云和从阿里云获取升级包的流程非常的熟悉了。所以本章我们进行STM32的程序开发…...

如何利用快照与备份快速恢复服务器的数据
在服务器上利用**快照(Snapshot)**和**备份(Backup)**快速恢复数据,可显著减少停机时间并确保业务连续性。以下是具体操作步骤和最佳实践: --- ### **1. 快照(Snapshot)恢复** **适…...

【Leetcode 每日一题】2799. 统计完全子数组的数目
问题背景 给你一个由 正 整数组成的数组 n u m s nums nums。 如果数组中的某个子数组满足下述条件,则称之为 完全子数组 : 子数组中 不同 元素的数目等于整个数组不同元素的数目。 返回数组中 完全子数组 的数目。 子数组 是数组中的一个连续非空序…...
)
主流操作系统对比分析(macOS、Linux、Windows、Unix)
主流操作系统对比分析(macOS、Linux、Windows、Unix) 一、系统基本介绍 系统核心特点典型代表macOS苹果公司开发,基于 Unix(BSD),闭源,专为苹果硬件优化,强调用户体验和设计美学。m…...

Qt使用 SQLite 数据库的基本方法
在 Qt 中,使用 SQLite 数据库的基本方法与 MySQL 类似,但 SQLite 是一个轻量级的嵌入式数据库,通常不需要外部数据库服务器。你可以直接在本地磁盘上操作 SQLite 数据库文件。 1. 安装 SQLite 驱动 通常,Qt 默认包含了对 SQLite…...

【刷题系列】LeetCode消失的数字、轮转数组
文章目录 1、消失的数字1.1 题目描述1.2 题目分析 2、轮转数字2.1 题目描述2.2 题目分析 1、消失的数字 原题链接:消失的数字 1.1 题目描述 数组nums包含从0到n的所有整数,但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗…...

Unreal Niagara制作SubUV贴图翻页动画
SubUV翻页动画是游戏中的常见功能,通过对每一小块UV进行移动可以模拟动画效果,接下来对下图进行SubUV动画的制作。 (金币测试图下载地址:https://download.csdn.net/download/grayrail/90684422) 最终效果如下: 1.…...

【C++】模版初阶:函数模板、类模板
文章目录 一、为什么要使用模板二、什么是函数模板1、函数模板(1)概念(2)格式(3)原理(4)函数模板的实例化(5)模板参数的匹配原则 2、类模板(1&…...
)
Kotlin基础知识全面解析(下)
文章目录 第六章:集合与函数式编程6.1 集合概述6.2 集合操作6.3 序列 第七章:协程与异步编程7.1 协程基础7.2 挂起函数7.3 异步与等待7.4 协程上下文与调度器 第八章:Kotlin标准库8.1 作用域函数let函数run函数with函数apply函数also函数 8.2…...

NVIDIA高级辅助驾驶安全报告解析
近期参加了NVIDIA高级辅助驾驶开发者实验室,读了NVIDIA的高级辅助驾驶安全报告白皮书,里面涉及了不少有意思的内容,大致分享下英伟达在高级辅助驾驶领域的安全性上的工作。 最令人印象深刻的是NVIDIA提出的"四大支柱"架构&#x…...

HarmonyOS:一多能力介绍:一次开发,多端部署
概述 如果一个应用需要在多个设备上提供同样的内容,则需要适配不同的屏幕尺寸和硬件,开发成本较高。HarmonyOS 系统面向多终端提供了“一次开发,多端部署”(后文中简称为“一多”)的能力,可以基于一种设计…...
