数据结构与算法学习笔记(Acwing提高课)----动态规划·数字三角形
数据结构与算法学习笔记----动态规划·数字三角形
@@ author: 明月清了个风
@@ first publish time: 2025.4.23ps⭐️终于开始提高课的题啦,借的人家的号看,以后给y总补票叭,提高课的题比之前的多很多啊哈哈哈哈,基本上每种题型都对应了难度逐步上升的几道题,和基础课的题相比加了一层应用,需要从题目中抽象出模型才能解题。
数字三角形的题为动态规划的经典模型,基础课中已经讲过了,在这里。提高课的是在此基础上的进一步延伸和应用,但原理其实没有变。
Acwing 1015. 摘花生
Hello Kitty想摘点花生送给她喜欢的米老鼠。
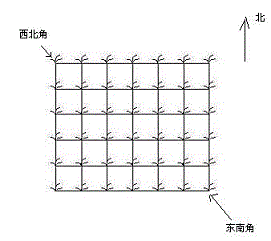
她来到一片有网格状道路的矩形花生地(如下图),从西北角进去,东南角出来。
地里每个道路的交叉点上都有种着一株花生苗,上面有若干颗花生,经过一株花生苗就能摘走该它上面所有的花生。
Hello Kitty只能向东或向南走,不能向西或向北走。
问Hello Kitty最多能够摘到多少颗花生。
输入格式
第一行是一个整数 T T T,代表一共有多少组数据。
接下来是 T T T组数据。
每组数据的第一行是两个整数,分别代表花生苗的行数 R R R和列数 C C C。
每组数据的接下来 R R R行数据,从北向南依次描述每行花生苗的情况。每行数据有 C C C个整数,按从西向东的顺序描述了该行每株花生苗上的花生数目 M M M。
输出格式
对每组输入数据,输出一行,内容为Hello Kitty能摘到得最多的花生颗数。
数据范围
1 ≤ T ≤ 100 1 \le T \le 100 1≤T≤100,
1 ≤ R , C ≤ 100 1 \le R,C \le 100 1≤R,C≤100,
0 ≤ M ≤ 1000 0 \le M \le 1000 0≤M≤1000
思路
对于动态规划而言,和基础课一样,考虑状态表示和状态转移。
对于状态表示,使用f[i][j],表示的集合是所有从(1, 1)走到(i, j)的路线,而要求的属性是这个集合中的最大值。
对于状态转移或者说状态计算,就是将上述集合进行划分,找出其子集递归求解。而状态划分的很重要的一种方法就是根据最后一步操作进行划分,也就是f[i][j]是怎么来的这一步。在这一题中,f[i][j]可以是从上面下来,也可以是从左边过来,因此可以划分为两个子集f[i][j - 1]和f[i - 1][j]。需要注意的是,对于集合的划分,最重要的两个原则是不重不漏,其中不漏是任何情况都需要满足的,因为每种方案都需要考虑,而不重在求最大值或最小值时可以不满足,因为重复的计算并不会提高集合中的最值。
在上面已经将集合f[i][j]划分为两个集合f[i - 1][j]和f[i][j - 1],那么求f[i][j]的最大值就是求这两个子集的最大值再加上最后一步的权值即可。
代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>using namespace std;const int N = 110;int T;
int n, m;
int a[N][N];
int f[N][N];int main()
{cin >> T;while(T --){cin >> n >> m;for(int i = 1; i <= n; i ++)for(int j = 1; j <= m; j ++)cin >> a[i][j];for(int i = 1; i <= n; i ++)for(int j = 1; j <= m; j ++)f[i][j] = max(f[i - 1][j], f[i][j - 1]) + a[i][j];cout << f[n][m] << endl;}return 0;
}
Acwing 1018. 最低通行费
一个商人穿过一个 N × N N \times N N×N的正方形的网格,去参加一个非常重要的商务活动。他要从网格的左上角进,右下角出。每穿越中间1个小方格,都要花费1个单位时间。商人必须在 2 N − 1 2N - 1 2N−1个单位时间穿越出去。而在经过中间的每个小方格时,都需要缴纳一定的费用。
这个商人期望在规定时间内用最少费用穿越出去。请问至少需要多少费用?
注意:不能对角穿越各个小方格(即,只能向上下左右四个方向移动且不能离开网格)。
输入格式
第一行是一个整数 T T T,表示正方形的宽度 N N N。
后面 N N N行,每行 N N N个不大于 100 100 100的整数,为网格上每个小方格的费用。
输出格式
输出一个整数,表示至少需要的费用。
数据范围
1 ≤ N ≤ 100 1 \le N \le 100 1≤N≤100
思路
其实还是和数字三角形一样的模型,只是多了个迷惑的地方,给了步骤限制为 2 N − 1 2N - 1 2N−1,但是可以发现只要不回头走就行。因此思路和代码都是和上面一样的。
需要注意的地方时,这一题求的集合的属性是最小值,因此需要对边界的地方进行特判和初始化。
代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>using namespace std;const int N = 110, inf = 1e9;int n;
int f[N][N];
int a[N][N];int main()
{cin >> n;for(int i = 1; i <= n; i ++)for(int j = 1; j <= n; j ++)cin >> a[i][j];for(int i = 1; i <= n; i ++)for(int j = 1; j <= n; j ++){if(i == 1 && j == 1) f[i][j] = a[i][j];else{f[i][j] = inf;if(i > 1) f[i][j] = min(f[i][j], f[i - 1][j] + a[i][j]);if(j > 1) f[i][j] = min(f[i][j], f[i][j - 1] + a[i][j]);}}cout << f[n][n] << endl;return 0;
}Acwing 1027. 方格取数
设有N*N的方格图( N ≤ 10 N \le 10 N≤10),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字0。
某人从图的左上角的 A A A点 ( 1 , 1 ) (1, 1) (1,1)出发,可以向下行走,也可以向右走,直到到达右下角的B点 ( N , N ) (N, N) (N,N)。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字0)。
此人从 A A A点到 B B B点共走两次,试找出2条这样的路径,使得取得的数之和为最大。
输入格式
第一行是一个整数 N N N,表示 N × N N \times N N×N的方格图。
接下来每行有三个整数,第一个为行号数,第二个为列号数,第三个为在该行、该列上所放的数。
一行以"0 ,0 ,0"表示结束。
输出格式
给出一个整数,表示两条路径上取得的最大的和。
数据范围
$ N \le 10$
思路
这一题的变化是要走两次。对于上面两题而言都只需要计算一个路径,而走两次最大的变化就是同一个数只能被拿走一次。
首先思考是两条路线一起走还是两条路线先后走,因为每个数只能拿一次,因此两条路线是完全独立的两条线,先走后走并不影响总和。可以直接对上面的状态表示进行推广,使用f[i1][j1][i2][j2]表示第一条路线走到了a[i1][j1],第二条路线走到了a[i2][j2]的集合。
然后就是如何不重复走到同一个格子,因为不能回头走,所以如果两条线走到了同一个格子,那么肯定有 i 1 + j 1 = i 2 + j 2 i_1 + j_1 = i_2 + j_2 i1+j1=i2+j2。
因此就有了下面的优化,上面这个状态表示是四维的,虽然数据范围很小,但是仍有优化空间,考虑到要对每个格子的坐标的和作比较,因此使用f[k][i1][i2]进行表示,其中k表示横纵坐标的和,那么就有j1 = k - i1和j2 = k - i2,当i1 == i2时,可能出现两条路线重合。
对于状态划分来说,和之前的题目一样,使用最后一步进行划分,只是这里会有两条路线。因此可以根据第一条路线向右或向下,第二条路线向右或向下分为四类:下下,下右,右下,右右。
以下下的组合为例说明状态计算方法:
- 对于下下的组合来说,两条路线都是向下走到了最新的一步,因此是分别从
a[i1][j1 - 1]和a[i2][j2 - 1]走到了最新位置,这两个地方的状态可以由 f [ k − 1 ] [ i 1 ] [ i 2 ] f[k - 1][i1][i2] f[k−1][i1][i2]表示,然后判断一下是否重合即可,重合的话那就只加上一个a[i1][j1]即可,不重合就要同时加上a[i1][j1]和a[i2][j2]。
代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>using namespace std;const int N = 20;int n;
int f[N * 2][N][N];
int w[N][N];int main()
{cin >> n;int a, b, c;while(cin >> a >> b >> c, a || b || c) w[a][b] = c;for(int k = 2; k <= n + n; k ++)for(int i1 = 1; i1 <= n; i1 ++)for(int i2 = 1; i2 <= n; i2 ++){int j1 = k - i1, j2 = k - i2;if(j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n){int t = w[i1][j1];if(i1 != i2) t += w[i2][j2];int &x = f[k][i1][i2];x = max(x, f[k - 1][i1- 1][i2 - 1] + t);x = max(x, f[k - 1][i1 - 1][i2] + t);x = max(x, f[k - 1][i1][i2 - 1] + t);x = max(x, f[k - 1][i1][i2] + t);}}cout << f[n + n][n][n] << endl;return 0;
}
Acwing 275. 传纸条
小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题。
一次素质拓展活动中,班上同学安排坐成一个 m m m行 n n n列的矩阵,而小渊和小轩被安排在矩阵对角线的两端,因此,他们就无法直接交谈了。
幸运的是,他们可以通过传纸条来进行交流。
纸条要经由许多同学传到对方手里,小渊坐在矩阵的左上角,坐标 ( 1 , 1 ) (1, 1) (1,1),小轩坐在矩阵的右下角,坐标 ( m , n ) (m, n) (m,n)。
从小渊传到小轩的纸条只可以向下或者向右传递,从小轩传给小渊的纸条只可以向上或者向左传递。
在活动进行中,小渊希望给小轩传递一张纸条,同时希望小轩给他回复。
班里每个同学都可以帮他们传递,但只会帮他们一次,也就是说如果此人在小渊递给小轩纸条的时候帮忙,那么在小轩递给小渊的时候就不会再帮忙,反之亦然。
还有一件事情需要注意,全班每个同学愿意帮忙的好感度有高有低(注意:小渊和小轩的好心程度没有定义,输入时用 0 0 0表示),可以用一个 0 ∼ 100 0 \sim 100 0∼100的自然数来表示,数越大表示越好心。
小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条,即找到来回两条传递路径,使得这两条路径上同学的好心程度之和最大。
现在,请你帮助小渊和小轩找到这样的两条路径。
输入格式
第一行有 2 2 2个用空格隔开的整数 m m m和 n n n,表示学生矩阵有 m m m行 n n n列。
接下来 m m m行是一个 m × n m \times n m×n的矩阵,矩阵中第 i i i行 j j j列的整数表示坐在第 i i i行 j j j列的学生的好心程度,每行的 n n n个整数之间用空格隔开。
输出格式
输出一个整数,表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。
数据范围
1 ≤ n , m ≤ 50 1 \le n, m \le 50 1≤n,m≤50
思路
这一题与上一题的区别是同一个格子不能走第二次,在上一题中,如果走到了重合的格子会少加一次权重,而这里要求是不能走第二次,其实也很好解决,也就是要证明有两条不相交的路线具有最大的好心程度之和。
首先要解决的是两条路线相交的问题,如果存在两条相交的路线,如下图所示,从A到B的两条路线中有两个交点C与D。

因为经过的格子的权重是确定的,因此可以对两条路线上的部分片段进行交换,变换后入下图:

因此得证相交的路线可以通过路线的变形使其变成等效但仅有相交点而不相错的情况。
根据题意,同一个点不能走第二次,因此考虑如何处理相交点 C C C和 D D D。通过观察上图可以发现,对于重合点C来讲,该路线可以转化为下图所示经过点E的路线,且该路线的好心程度之和一定优于原路线(将重合点C权重清零后第二次不再计算)

根据上一题的代码可以发现,其实当走到同一点时,我们只会添加一次权重,因此这里的值一定会比经过点E的路线值小,也就是题目所限制的非法路线算出来的值一定小于最优解合法路的值,因此上一题的代码中不必为了这一题进行修改,代码稍有变动。
代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>using namespace std;const int N = 60;int n, m;
int f[N * 2][N][N];
int w[N][N];int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++)for(int j = 1; j <= m; j ++)cin >> w[i][j];for(int k = 2; k <= n + m; k ++)for(int i1 = 1; i1 <= n; i1 ++)for(int i2 = 1; i2 <= n; i2 ++){int j1 = k - i1, j2 = k - i2;if(j1 >= 1 && j1 <= m && j2 >= 1 && j2 <= m){int t = w[i1][j1];if(i1 != i2) t += w[i2][j2];int &x = f[k][i1][i2];x = max(x, f[k - 1][i1- 1][i2 - 1] + t);x = max(x, f[k - 1][i1 - 1][i2] + t);x = max(x, f[k - 1][i1][i2 - 1] + t);x = max(x, f[k - 1][i1][i2] + t);}}cout << f[n + m][n][n] << endl;return 0;
}
相关文章:
----动态规划·数字三角形)
数据结构与算法学习笔记(Acwing提高课)----动态规划·数字三角形
数据结构与算法学习笔记----动态规划数字三角形 author: 明月清了个风 first publish time: 2025.4.23 ps⭐️终于开始提高课的题啦,借的人家的号看,以后给y总补票叭,提高课的题比之前的多很多啊哈哈哈哈,基本上每种题型都对应了…...
debugfs文件系统及常见调试节点介绍)
RK3568平台开发系列讲解(调试篇)debugfs文件系统及常见调试节点介绍
更多内容可以加入Linux系统知识库套餐(教程+视频+答疑) 🚀返回专栏总目录 文章目录 一、什么是debugfs二、/proc/filesystems三、debugfs的挂载3.1、fstab 的文件结构3.2、手动挂载与卸载四、debugfs 常见目录有哪些4.1、/sys/kernel/debug/gpio4.2、/sys/kernel/debug/…...

数字化转型避坑指南:中钧科技如何用“四个锚点”破解转型深水区
数字化转型浪潮下,企业常陷入四大典型陷阱:跟风式投入、数据沼泽化、流程伪在线、安全裸奔化。中钧科技旗下产品以“经营帮”平台为核心,通过针对性方案帮助企业绕开深坑。 陷阱一:盲目跟风,为数字化而数字化 许…...

数字化转型下的批发订货系统:降本增效的关键路径
随着数字化转型的不断深入,越来越多的企业开始拥抱现代化的技术和工具,以提升业务效率、降低运营成本。批发行业,作为一个高度依赖库存和订单管理的行业,数字化转型尤为关键。传统的批发订货系统存在信息不对称、操作复杂、效率低…...

一 、环境的安装 Anaconda + Pycharm + PaddlePaddle
《从零到一实践:系统性学习生成式 AI(NLP)》 一 、环境的安装 Anaconda Pycharm PaddlePaddle 1. Anaconda 软件安装 Anaconda 软件安装有大量的教程,此处不在说明,安装完成之后界面如下: 2. 创建 Anaconda 虚拟环境 Paddl…...

Dhtmlx Gantt教程
想实现的效果 插件安装: npm i dhtmlx-gantt使用该插件的时候,直接导入包和对应的样式即可: import { Gantt} from "dhtmlx-gantt"; import "dhtmlx-gantt/codebase/dhtmlxgantt.css";也可以安装试用版本,…...

大模型框架技术全景与下一代架构演进
一、大模型框架概述 大模型框架是支撑千亿级参数模型训练、推理及产业落地的技术底座,涵盖分布式计算、高效内存管理、多模态融合等核心模块。从GPT-3到Gemini Ultra,大模型框架的迭代推动AI从“作坊式实验”迈向“工业化生产”。据Gartner预测&a…...

官方不存在tomcat10-maven-plugin插件
Maven 中央仓库中没有官方的tomcat10-maven-plugin。Apache Tomcat Maven 插件项目目前仅对以下插件提供官方支持: tomcat6-maven-plugin tomcat7-maven-plugin tomcat8-maven-plugin tomcat9-maven-plugin 如果你想使用 cargo 命令来跑支持 Jakarta EE 的 Tomcat 1…...

vue3 el-table 右击
在 Vue 3 中使用 Element Plus 的 <el-table> 组件时,如果你想实现右击(右键点击)事件的处理,你可以通过监听 contextmenu 事件来实现。contextmenu 事件在用户尝试打开上下文菜单(通常是右键点击)时…...

第一节:核心概念高频题-Vue3响应式原理与Vue2的区别
Vue2:基于Object.defineProperty监听对象属性,需手动处理数组方法重写 Vue3:采用Proxy代理实现全量响应式,支持动态新增属性和深层嵌套对象监听 一、实现机制对比 1. Vue2:基于 Object.defineProperty • 原理&#…...
)
【锂电池剩余寿命预测】CNN卷积神经网络锂电池剩余寿命预测(Pytorch完整源码和数据)
目录 效果一览程序获取程序内容代码分享效果一览 程序获取 获取方式一:文章顶部资源处直接下载:...

web刷题笔记
2024isctf ezrce 禁用了一些关键字符,查询函数,系统执行函数,执行函数都有,空格也和斜杆也禁用了,但是其他一些很大一部分字符都没有禁用,属于关键词禁用的类型,正常的步骤是去查一下列表&#…...

基于FPGA 和DSP 的高性能6U VPX 采集处理板
基于FPGA 和DSP 的高性能6U VPX 采集处理板,是一款处理架构采用FPGADSP 的高性能的6U VPX 采集处理板。板载4 片高速ADC 共8 个采集通道,可支持8 路采样率最高2.6Gsps/14Bit 的模拟信号通道。 板卡FPGA 采用Xilinx 公司KU 系列的XCKU115-2FLVF1924I&…...

uniapp中使用<cover-view>标签
文章背景: uniapp中遇到了原生组件(canvas)优先级过高覆盖vant组件 解决办法: 使用<cover-view>标签 踩坑: 我想实现的是一个vant组件库中动作面板的效果,能够从底部弹出框,让用户进行选择,我直…...

【JavaScript】详讲运算符--算术运算符
1、运算符简介 运算符也叫操作符,通过运算符可以对一个或多个值进行运算,比如:typeof就是运算符,可以来获得一个值的类型,它会将该值的类型以字符串的形式返回,即:typeof 变量名的结果为字符串类型。 <…...

.NET 6 + Dapper + User-Defined Table Type
大家都知道,对于SQL Server IN是有限制条件的,如果IN里面的内容过多,在执行的时候会被自动截断,因而导致查询到的结果不是实际需要的结果。 select * from Payments where Id in (1,2,3,4,...) 为了解决上面的限制,可以…...

使用 Conda 创建新环境
使用 Conda 创建新环境 在使用 Conda 进行包管理和环境隔离时,创建新环境是一个非常常见的操作。通过创建独立的环境,可以避免不同项目之间的依赖冲突,并且能够灵活地管理各个项目的运行环境。 以下是使用 Conda 创建和管理新环境的详细步骤…...

数据为基:机器学习中数值与分类数据的处理艺术及泛化实践
数据为基:机器学习中数值与分类数据的处理艺术及泛化实践 摘要 在机器学习实践中,数据质量对模型效果的影响往往超过算法选择。本文通过详实的案例解析,系统阐述数值型数据与分类数据的特征工程处理方法,揭示数据预处理对模型泛…...

Docker镜像与容器概念解析
Docker镜像与容器概念解析 -更适合大学生宝宝体制的docker学习指南 一、Docker镜像:应用程序的基因库 (1)本质特征:镜像是一个只读的二进制文件包,相当于应用程序的”基因图谱”。就像生物体的DNA决定了生物特征&a…...

基于GMM的语音识别
语音识别是近年来发展非常迅速的一项计算机智能技术,广泛应用在语音控制、身份识别等多个领域。本次项目主要研究语音识别的预处理过程和特征参数的提取环节。通过对原始语音信号进行预加重和分帧、加窗,滤除低频干扰,提升对语音识别有用的部…...

K8S安全认证
一。用户认证的基本框架 在K8S集群中,客户端通常有两类: 1.User Account:一般独立于K8S之外的其他服务管理的用过户账号 2.Service Account:K8S管理的账号,用于为Pod中的服务进程在访问K8S提供身份标识 ApiServer是…...

咖啡机语音芯片方案-WTN6040FP-14S直接驱动4欧/3W喇叭-大功率输出
一、开发背景 随着智能家居市场的快速发展和消费者对家电产品交互体验要求的不断提高,语音提示功能已成为现代咖啡机产品的重要卖点之一。传统咖啡机仅依靠指示灯和简单蜂鸣器提示,无法满足用户对操作引导、状态反馈和个性化体验的需求。 WTN6040FP-14大…...

Vue3集成百度实时语音识别
示例 SpeechRecognitionModal.vue 组件 <template><transition name"modal-fade"><div v-if"isOpen" class"modal-overlay" click.self"handleOverlayClick"><div class"modal-container"><div…...

C# 设计原则总结
跟着视频学习的,记录一下最后的总结。 接口隔离: 单一职责: 里氏替换: 依赖倒置; 迪米特法则; 开闭原则:...

zkPass案例实战之合约篇
目录 一、contracts/contracts/ProofVerifier.sol 1. License 和 Solidity 版本 2. 导入依赖 3. 合约声明和默认分配器地址 4. 验证证明 5. 验证分配器签名 6. 验证验证者签名 7. 签名前缀处理 8. 签名恢复 总结 二、contracts/contracts/SampleAttestation.sol 1. …...

docker学习笔记5-docker中启动Mysql的最佳实践
一、查找目录文件位置 1、mysql的配置文件路径 /etc/mysql/conf.d 2、mysql的数据目录 /var/lib/mysql 3、环境变量 4、端口 mysql的默认端口3306。 二、启动命令 1、启动命令说明 docker run -d -p 3306:3306 -v /app/myconf:/etc/mysql/conf.d # 挂载配置目录 -v…...

彻底禁用windows的语音识别快捷键win+ctrl+s
工作中经常使用ctrls保存,但是经常误触win,结果弹出如下对话框,甚是闹心: 搜索网络,问AI,竟然没有一个好用的不依赖常驻内存软件的办法,最终经过探索与验证,总算是彻底解决了此问题&…...
-Analytic函数集)
大数据学习(112)-Analytic函数集
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言📝支持一…...

文档构建:Sphinx全面使用指南 — 实战篇
文档构建:Sphinx全面使用指南 — 实战篇 Sphinx 是一款强大的文档生成工具,使用 reStructuredText 作为标记语言,通过扩展兼容 Markdown,支持 HTML、PDF、EPUB 等多种输出格式。它具备自动索引、代码高亮、跨语言支持等功能&#…...
安装移动磐维数据库(PanWeiDB_V2.0-S2.0.2_B01)步骤)
欧拉环境(openEuler 22.03 LTS SP3)安装移动磐维数据库(PanWeiDB_V2.0-S2.0.2_B01)步骤
一、磐维数据库概述 中国移动磐维数据库(ChinaMobileDB),简称“磐维数据库”(PanWeiDB),是中国移动信息技术中心首个基于中国本土开源数据库打造的面向ICT基础设施的自研数据库产品。其产品内核能力基于华…...

【产品经理从0到1】产品规划
产品规划 已经知道要做什么功能,展示什么信息,那这些信息应该 以什么方式展现给用户? 信息架构的概念 一般的商场导览图,都有以下特征: • 每一层都由多个店铺组成; • 商场有出口,有入口&am…...

一篇文章学会开发第一个ASP.NET网页
*开发环境:Visual Studio 2022 ASP.NET Core 6.0* 一、开发环境准备 1.1 安装必备工具 Visual Studio 2022 Community(免费版本) .NET 6.0 SDK 验证安装:命令行执行 dotnet --version 显示6.0.x版本 1.2 创建新项目 打开VS…...
)
[架构之美]Ubuntu源码部署APISIX全流程详解(含避坑指南)
[架构之美]Ubuntu源码部署APISIX全流程详解(含避坑指南) 一、离线安装场景需求分析 1.1 典型应用场景 金融/政务内网环境生产环境安全合规要求边缘计算节点部署1.2 离线安装难点 #mermaid-svg-B25djI0XquaOb1HM {font-family:"trebuchet ms",verdana,arial,sans-s…...
)
【3】CICD持续集成-k8s集群中安装Jenkins-agent(主从架构)
一、背景: Jenkins Master/Slave架构,Master(Jenkins本身)提供Web页面让用户来管理项目和从节点(Slave),项目任务可以运行在Master本机或者分配到从节点运行,一个Master可以关联多个…...

2024从Maven-MySQL-Nginx部署
1、IDEA配置全局Maven设置 第一步:File->Close Project返回到创建工程界面。 第二步:找到bulid---maven设置对应位置。 第三步:选中两栏后的Override---应用---关闭即可。 *************************************************************…...

MySQL运算符
目录 一、mysql运算符 1. 算数运算符 2. 比较运算符 2.1 等号运算符() 2.2 不等于运算符 ! 3.非符号类型的运算符 3.1 空运算 IS NULL、 IS NOT NULL、 ISNULL 3.2 区间查询 BETWEEN 3.3 包含查询 IN、 NOT IN 3.4模糊查询LIKE 4. 逻辑运算符 4.1 AND(逻…...

什么是区块?
“区块”是区块链技术的基本组成部分,是加密货币交易的数字记录簿。一个区块就像是账本中的一页,详细记录了所有的交易细节。每个区块都包含基本信息,如最近的交易列表、标记区块创建时间的时间戳,以及称为“哈希值”的唯一加密代…...

爬虫学习——获取动态网页信息
对于静态网页可以直接研究html网页代码实现内容获取,对于动态网页绝大多数都是页面内容是通过JavaScript脚本动态生成(也就是json数据格式),而不是静态的,故需要使用一些新方法对其进行内容获取。凡是通过静态方法获取不到的内容,…...

LSA六种类型
LAS --- 链路状态通告 链路状态类型、链路状态ID、通告路由器 --- LSA的三元组 --- 可以唯一标识出一条LSA Type --- OSPFv2中,常见的需要掌握LSA有6种 LS ID --- LSA的名字 --- 因为每一种LSA ID的生成方式都不相同,所以导致可能重复,则如…...

第七篇:linux之基本权限、进程管理、系统服务
第七篇:linux之基本权限、进程管理、系统服务 文章目录 第七篇:linux之基本权限、进程管理、系统服务一、基本权限1、什么是权限?2、为什么要有权限?3、权限与用户之间的关系?4、权限对应的数字含义5、使用chmod设定权…...

时序约束 记录
一、基础知识 1、fpga的约束文件为.fdc,synopsys的约束文件为.sdc。想通过fpga验证soc设计是否正确,可以通过syn工具(synplify)吃.fdc把soc code 转换成netlist。然后vivado P&R工具通过吃上述netlist、XDC 出pin脚约束、fdc时序约束三个约束来完成…...

fpga系列 HDL:跨时钟域同步 脉冲展宽同步 Pulse Synchronization
Pulse Synchronization 脉冲同步(Pulse Synchronization)是 FPGA 设计中处理跨时钟域信号传输的常见问题和关键细节。由于不同步的时钟域之间可能存在相位差或频率差异,可能会导致亚稳态问题或数据丢失。脉冲同步的主要目标是确保一个时钟域中…...

链表系列一>两数相加
目录 题目:解析:方法:代码:链表常用技巧: 题目: 链接: link 解析: 方法: 代码: /*** Definition for singly-linked list.* public class ListNode {* int val;* …...

MCP接入方式介绍
上一篇文章,我们介绍了MCP是什么以及MCP的使用。 MCP是什么,MCP的使用 接下来,我们来详细介绍一下MCP的接入 先看官网的架构图 上图的MCP 服务 A、MCP 服务 B、MCP 服务 C是可以运行在你的本地计算机(本地服务器方式ÿ…...

嵌入式WebRTC音视频实时通话EasyRTC助力打造AIOT智能硬件实时通信新生态
一、背景 在当今智能化时代,智能硬件设备正迅速融入人们的生活和工作中,从智能家居、智能穿戴到工业物联网,智能硬件的应用场景不断拓展。实时通信技术作为智能硬件的重要组成部分,能够实现设备之间的无缝连接和交互。基于WevRTC…...

Linux的进程间通信
目录 进程间通信介绍 进程间通信的概念 主要IPC方式 进程间通信的目的 进程间通信的本质 进程间通信的分类 管道 什么是管道 匿名管道 匿名管道的原理 pipe函数 匿名管道使用步骤 管道读写规则 匿名管道的特点 管道的四种特殊情况 管道的大小 命名管道 命名管…...
)
基于nodeJS代码的通过爬虫方式实现tiktok发布视频(2025年4月)
1、将真实的tiktokstudio平台的cookie填到代码里的cookie变量里,修改python代码里的ticket,ts, privateKey,以及videoPath,timing等变量的值,最后运行python脚本即可; 2、运行之前根据import提示安装一些常见依赖,比如node-fetch等; 3、运行时候可能系统需要科学上网…...

邮件被标记为垃圾邮件怎么办
1. 找出问题原因 先看看邮件内容有没有用到像“免费”“促销”这类容易触发垃圾邮件过滤的词,或者格式是不是太乱(比如图片太多、代码复杂等)。再确认一下发件人地址或IP有没有上黑名单,可以用工具查一查。 2. 修复发件人信誉 …...

视频监控从安装到优化的技术指南,视频汇聚系统EasyCVR智能安防系统构建之道
在当今数字化安防时代,监控系统的安装与配置对于保障各类场所的安全起着至关重要的作用。从前期规划到实际安装,再到后期的功能实现与维护,每一个环节都不容小觑。本文将详细阐述监控安装过程中的关键要点,并结合EasyCVR平台功能&…...

.NET 6 WPF 利用CefSharp.Wpf.NETCore显示PDF文件
在WPF程序中,我们可以有多种方式显示PDF文件,但是目前发现的性能最好的是CefSharp.Wpf.NETCore。 CefSharp.Wpf.NETCore是一款开源软件。https://github.com/cefsharp/CefSharp。 它提供了WPF版本和WinForm版本,可根据自己的需要进行安装。…...
