6.8.最小生成树

一.复习:
1.生成树:

对于一个连通的无向图,假设图中有n个顶点,如果能找到一个符合以下要求的子图:
子图中包含图中所有的顶点,同时各个顶点保持连通,
而且子图的边的数量只有n-1条,
那么这样的子图就是生成树,一个连通图可能有多个生成树。
2.广度优先生成树:

3.深度优先生成树:

二.最小生成树(最小代价树):生成树必须包含图中所有的顶点
1.前言:

假设有一个城市叫P城,P城周围规划了学校、农场、电站、渔村、矿场,
各个地方之间有上图所示的修路方案,其中数字表示修路的成本,比如修一条P城和学校之间的路需要1块钱,修一条学校和矿场之间的路需要5块钱,
现在为了节省P城的财政支出,没有必要把所有的可行的道路都修一遍,
因此需要制定一个修路方案,这个方案要求所有地方都是连通的即各个地方之间是相互可到达的(各个地方之间不一定是相邻的),但是成本又必须降到最低,此时有如下两种方案:

左边的方案可以使得各个地方连通,代价是20块钱(图片打错了);
右边的方案也可以使各个地方连通,但代价是16块钱,
但是否有更便宜的方案呢?这就是最小生成树(最小代价树)要研究的问题。
对于带权的连通图,它可以有多个生成树,我们要从所有的生成树当中找出各个边的权值之和最小即代价最小的那棵树,这个树就是最小生成树。
2.概念:
注:最小生成树研究的是带权的连通无向图。

3.特例:当带权连通的无向图的权值都为一个数
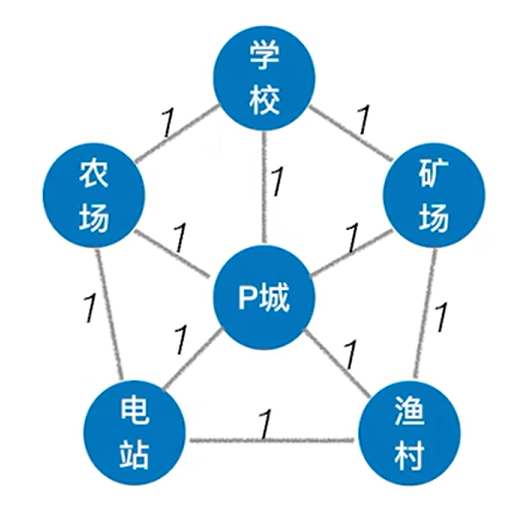
以上述图片的带权连通无向图为例,可得出如下两个生成树:

由生成树的概念可知这两棵生成树的边都是5条(边等于顶点总数减一,此时有6个顶点),由于每一条边的权值都为1,因此这两棵生成树所有边的权值之和都为5,
由此可知本例中带权无向图的任意一棵生成树的所有边的权值之和都为5,因此最小的权值之和为5,
结论:假设一个带权连通无向图的顶点数为V个,边为E条,边的权值都为a,
该图的所有生成树都只有(V-1)条边,其权值之和为(V-1) * a,由此可知最小生成树的权值之和为(V-1) * a,因为所有树都一样。
4.性质:

-
如果一个连通图本身就是一棵树(树不存在环路),也就是图中各个顶点连通但不存在环,那么这个图的最小生成树就是它本身->因为如果连通图是树时,那么它已经是生成树了,而且无法再有更小的生成树了,再有的话就会缺顶点,不符合生成树的条件,所以此时这个图的最小生成树就是它本身
-
只有连通图才有生成树
-
对于非连通图,只会有生成森林,因为非连通图不止一个连通分量,生成的也就不止一个生成树,最终就是生成森林(这里生成必须要包括图中的所有顶点,不然不符合生成的条件)

5.总结:

三.求最小生成树-Prim算法(普里姆算法):
1.例一:

以上述图片为例,挑选图中任意一个顶点,从该顶点出发构建生成树:

如上图,比如从P城这个顶点出发构建生成树,之后每次将代价最小的新顶点纳入生成树,直到所有顶点都纳入为止,
此时要构建的生成树中只有P城这一个顶点,从P城出发,分别对比到达学校、矿场、渔村、电站、农场所需要的代价,可知从P城到达学校的代价最小,因此接下来要把学校这个顶点纳入生成树,如下图:

如上图,在当前生成树下重复刚才的步骤,此时的生成树中有P城和学校两个顶点,
现在要从P城或学校出发,在农场、电站、渔村、矿场中选择一个代价最小的顶点连到当前生成树中,
由上图可知最小的代价为4,如下图:

意味着可以把矿场或者渔村纳入生成树中,
此时先把矿场纳入生成树,如下图:

如上图,在当前生成树下重复刚才的步骤,此时的生成树中包括P城、学校和矿场,
现在要从P城或学校或矿场出发,在农场、电站、渔村中选择一个代价最小的顶点连到当前生成树中,
由上图可知最小的代价为2,如下图:

意味着把渔村纳入生成树中,如下图:

如上图,在当前生成树下重复刚才的步骤,此时的生成树中包括P城、学校、矿场和渔村,
现在要从P城或学校或矿场或渔村出发,在农场、电站中选择一个代价最小的顶点连到当前生成树中,
由上图可知最小的代价为5,如下图:

意味着把农场纳入生成树中,如下图:

如上图,在当前生成树下重复刚才的步骤,此时的生成树中包括P城、学校、矿场、渔村和农场,
现在要从P城或学校或矿场或渔村或农场出发,在电站中选择一个代价最小的顶点连到当前生成树中,
由上图可知最小的代价为3,如下图:
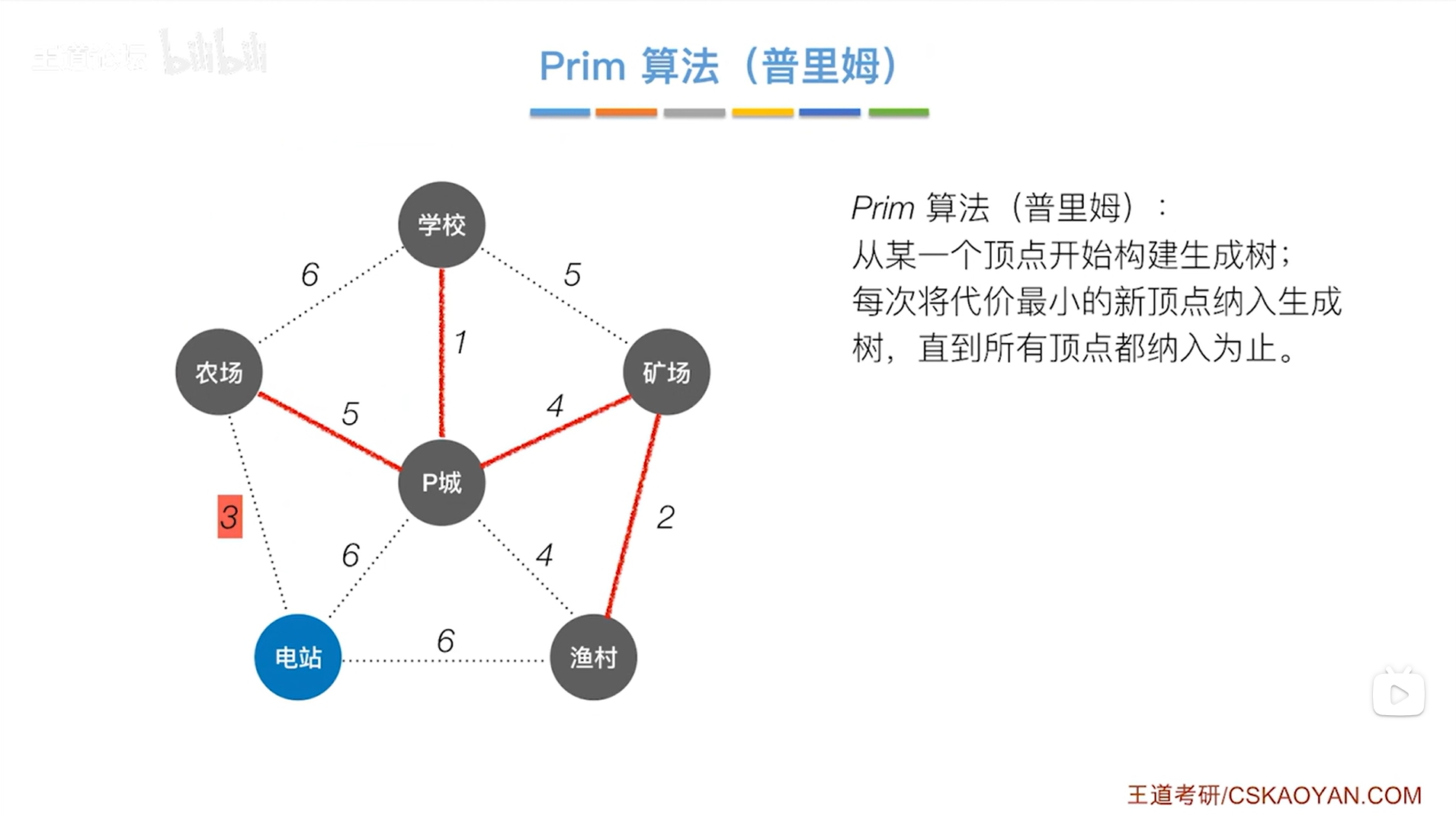
意味着把电站纳入生成树中,如下图:

如下图,最终得到了最小生成树:

也就是说按照如上图所得出的最小生成树进行施工的话,只需要付15块钱,也是最小代价。
2.例二:

以上述图片为例,挑选图中任意一个顶点,从该顶点出发构建生成树:

如上图,比如从P城这个顶点出发构建生成树,之后每次将代价最小的新顶点纳入生成树,直到所有顶点都纳入为止,
此时要构建的生成树中只有P城这一个顶点,从P城出发,分别对比到达学校、矿场、渔村、电站、农场所需要的代价,可知从P城到达学校的代价最小,因此接下来要把学校这个顶点纳入生成树,如下图:

如上图,在当前生成树下重复刚才的步骤,此时的生成树中有P城和学校两个顶点,
现在要从P城或学校出发,在农场、电站、渔村、矿场中选择一个代价最小的顶点连到当前生成树中,
由上图可知最小的代价为4,如下图:

意味着可以把矿场或者渔村纳入生成树中,
此时把渔村纳入生成树,如下图:

如上图,在当前生成树下重复刚才的步骤,此时的生成树中包括P城、学校、渔村,
现在要从P城或学校或渔村出发,在农场、电站、矿场中选择一个代价最小的顶点连到当前生成树中,
由上图可知最小的代价为2,如下图:

意味着把矿场纳入生成树中,如下图:

如上图,在当前生成树下重复刚才的步骤,此时的生成树中包括P城、学校、渔村、矿场,
现在要从P城或学校或渔村或矿场出发,在农场、电站中选择一个代价最小的顶点连到当前生成树中,
由上图可知最小的代价为5,如下图:

意味着把农场纳入生成树中,如下图:

如上图,在当前生成树下重复刚才的步骤,此时的生成树中包括P城、学校、渔村、矿场、农场,
现在要从P城或学校或渔村或矿场或农场出发,在电站中选择一个代价最小的顶点连到当前生成树中,
由上图可知最小的代价为3,如下图:

意味着把电站纳入生成树中,如下图:

如下图,最终得到了最小生成树:

也就是说按照如上图所得出的最小生成树进行施工的话,只需要付15块钱,也是最小代价。
3.对比例一与例二分别得出的最小生成树:

以上两棵生成树的最小代价都是15,
因此同一个图可能有多个最小生成树,虽然形态不同,但是这些最小生成树的所有边的权值之和都是一样且最小的。
4.例三:

以上述图片为例,挑选图中任意一个顶点,从该顶点出发构建生成树:

如上图,比如从农场这个顶点出发构建生成树,之后每次将代价最小的新顶点纳入生成树,直到所有顶点都纳入为止,
此时要构建的生成树中只有农场这一个顶点,从农场出发,分别对比到达学校、电站、渔村、矿场、P城所需要的代价,可知从农场到达电站的代价最小,因此接下来要把电站这个顶点纳入生成树,如下图:

如上图,在当前生成树下重复刚才的步骤,此时的生成树中有农场和电站两个顶点,
现在要从农场或电站出发,在渔村、矿场、学校、P城中选择一个代价最小的顶点连到当前生成树中,
由上图可知最小的代价为5,如下图,因此要把P城纳入生成树中:

如上图,在当前生成树下重复刚才的步骤,此时的生成树中有农场、电站、P城,
现在要从农场或电站或P城出发,在渔村、矿场、学校中选择一个代价最小的顶点连到当前生成树中,
由上图可知最小的代价为1,如下图,因此要把学校纳入生成树中:

如上图,在当前生成树下重复刚才的步骤,此时的生成树中有农场、电站、P城、学校,
现在要从农场或电站或P城或学校出发,在渔村、矿场中选择一个代价最小的顶点连到当前生成树中,
由上图可知最小的代价为4,如下图,因此可以把矿场或渔村纳入生成树中,此时把矿场纳入生成树中(这里把渔村纳入生成树后得出的最小生成树的最小代价一致):

如上图,在当前生成树下重复刚才的步骤,此时的生成树中有农场、电站、P城、学校、矿场,
现在要从农场或电站或P城或学校或矿场出发,在渔村中选择一个代价最小的顶点连到当前生成树中,
由上图可知最小的代价为2,如下图,因此可以把渔村纳入生成树中:

最终得出了如上图所示的最小生成树,最小代价也是15,与例一、例二的最小代价一样。
四.求最小生成树-Kruskal算法(克鲁斯卡尔):
实例:

执行过程:每次选择一条权值最小的边,使这条边的两头连通(原本已经连通的就不选),直到所有顶点连通。
以上述图片为例,一开始图里的各个顶点都独立存在,各个顶点之间不存在边,所以用虚线标注,
现在从所有的虚线里挑出权值最小的一条,显然权值最小的是1这条虚线,如下图:

如上图,1这条虚线的两头是P城和学校这两个顶点,这两个顶点此时还没有连通,所以把这条虚线选中,使这两个顶点连通,如下图:

如上图,继续从所有的虚线里挑出权值最小的一条,显然权值最小的是2这条虚线,如下图:

如上图,2这条虚线的两头是渔村和矿场这两个顶点,这两个顶点此时还没有连通,所以把这条虚线选中,使这两个顶点连通,如下图:

如上图,继续从所有的虚线里挑出权值最小的一条,显然权值最小的是3这条虚线,如下图:

如上图,3这条虚线的两头是农场和电站这两个顶点,这两个顶点此时还没有连通,所以把这条虚线选中,使这两个顶点连通,如下图:

如上图,继续从所有的虚线里挑出权值最小的一条,显然权值最小的是4这条虚线,如下图:

如上图,P城和矿场之间的虚线的权值、P城和渔村之间的虚线的权值都为4,现在选择P城和矿场之间的虚线,P城和矿场这两个顶点此时还没有连通,所以把这条虚线选中(P城和渔村这两个顶点此时也没有连通,所以选这条虚线也可以),使这两个顶点连通,最终P城、矿场、渔村、学校这几个顶点就都连通了,如下图:

如上图,继续从所有的虚线里挑出权值最小的一条,显然权值最小的是4这条虚线,如下图:

如上图,此时权值为4的这条虚线的两头是P城和渔村,由于P城和渔村这两个顶点已经连通了,所以这条虚线需要跳过不选,如下图:

如上图,继续从所有的虚线里挑出权值最小的一条,显然权值最小的是5这条虚线,如下图:

如上图,P城和农场之间的虚线的权值、学校和矿场之间的虚线的权值都为5,由于学校和矿场已经连通,因此学校和矿场之间的虚线不选,而P城和农场之间还没有连通,所以应选中P城和农场之间的虚线,如下图:

如上图,至此,所有的顶点全部连通,Kruskal算法(克鲁斯卡尔)结束。
如下图,本例采用Kruskal算法(克鲁斯卡尔)得出的最小生成树的最小代价为15,与用Prim算法(普里姆算法)得出的结果一致:

五.Prim算法(普里姆算法) v.s. Kruskal算法(克鲁斯卡尔):
假设图中有V个顶点、E条边:

对于Prim算法(普里姆算法),每一次是选择一个顶点开始;
对于Kruskal算法(克鲁斯卡尔),每一次是选择一条边开始;
因此这两个算法所表现出的时间复杂度也就不一样,
Prim算法(普里姆算法)的时间复杂度只与顶点的个数有关,适用于边稠密图即边多的图(因为边多的话顶点相对少一些),
Kruskal算法(克鲁斯卡尔)的时间复杂度只与边的个数有关,适用于边稀疏图即边少的图(因为边越少越能在短时间完成)。
六.Prim算法的实现思想:
1.实例:

以上述图片为例,假设从v0顶点开始,设置isJoin数组和lowCost数组:
isJoin数组用于记录图中的顶点是否被加入正在组建的生成树中,由于刚开始v0已经在生成树中,所以v0在isJoin数组的值为true(上述图片标记为勾),其余的顶点没有加入生成树中,因此其余的顶点对应的值都为false(上述图片标记为叉);
lowCost数组用于记录把这些顶点加入到已经组建的生成树里所需要花费的最低代价->最开始选中了v0,
由于v0与v0之间不存在边,所以v0对应的lowCost数组的值为0,
由于v0与v1之间有一条边,这条边的权值为6,因此把v1加入到组建的生成树中所需要付出的最低代价是6,所以v1对应的lowCost数组的值为6,
由于v0与v2之间有一条边,这条边的权值为5,因此把v3加入到组建的生成树中所需要付出的最低代价是5,所以v2对应的lowCost数组的值为5,
由于v0与v3之间有一条边,这条边的权值为1,因此把v2加入到组建的生成树中所需要付出的最低代价是1,所以v3对应的lowCost数组的值为1,
而v4与v5这两个顶点和v0之间都没有直接相连的边,所以就目前来看,暂时无法把v4、v5放到组建好的生成树中,因此v4与v5对应的lowCost的值都用无穷记录,也可以用别的记录。
如下图,开始进行第一轮处理:

首先需要检查isJoin数组和lowCost数组,最终找出一个还没有被加入生成树且代价最低的顶点,
由上述图片可知,v3顶点没有加入生成树中且代价最小,因此把v3顶点加入生成树中,如下图:

如上图,要把v3顶点在isJoin数组中对应的值修改为true即勾,表示已加入生成树中,继续如下图:

如上图,需要循环遍历lowCost数组,更新还没加入的各个顶点对应的lowCost值,
现在加入了v3这个顶点之后,对于其他的还没有被加入生成树的顶点,接下来加入生成树的代价有可能会改变,
因为生成树中相较于一开始多了个v3顶点,最开始只有v0顶点时加入v1顶点最低代价为6,现在多了个v3顶点,加入v1顶点的最低代价为5,显然小于6,因此接下来如果要把v1加到生成树中,所需要付出的最低代价就从6变成了5,
因此把v1对应的lowCost值修改为5,同理现在
加入v2的最低代价为4,因此把v2对应的lowCost值修改为4,
加入v4的最小代价为6,因此把v4对应的lowCost值修改为6,
加入v5的最小代价为4,因此把v5对应的lowCost值修改为4,
由于v0与v3这两个顶点已经加入到生成树中,所以对应的lowCost值无需修改(因为之后不会再加入v0与v3这两个顶点),
最终lowCost数组中的值依次为0、5、4、1、6、4,
如下图:

如下图,开始进行第二轮处理:原理与第一轮一样

首先需要检查isJoin数组和lowCost数组,最终找出一个还没有被加入生成树且代价最低的顶点,
由上述图片可知,v2顶点和v5顶点都没有加入生成树中且代价都是最小的(代价都为4),因此v2顶点和v5顶点都可以加入生成树中,但如果是从头到尾去扫描lowCost数组中的元素,v2顶点是第一个被挑选并加入生成树中的,如下图:

如上图,要把v2顶点在isJoin数组中对应的值修改为true即勾,表示已加入生成树中,继续如下图:

如上图,需要循环遍历lowCost数组,更新还没加入的各个顶点对应的lowCost值,
由上述图片可知,加入v2顶点之后,
加入v1的最低代价为5,无需修改,
加入v4的最小代价为6,无需修改,
加入v5的最小代价为2,因此把v5对应的lowCost值修改为2,
由于v0、v3和v2这三个顶点已经加入到生成树中,所以对应的lowCost值无需修改(因为之后不会再加入v0、v3和v2这三个顶点),
最终lowCost数组中的值依次为0、5、4、1、6、2,
如下图:

如下图,开始进行第三轮处理:

首先需要检查isJoin数组和lowCost数组,最终找出一个还没有被加入生成树且代价最低的顶点,
由上述图片可知,v5顶点没有加入生成树中且代价最小,因此把v5顶点加入生成树中,如下图:

如上图,要把v5顶点在isJoin数组中对应的值修改为true即勾,表示已加入生成树中,继续如下图:

如上图,需要循环遍历lowCost数组,更新还没加入的各个顶点对应的lowCost值,
由上述图片可知,加入v5顶点之后,
加入v1的最低代价为5,无需修改,
加入v4的最小代价为6,无需修改,
由于v0、v3、v2和v5这四个顶点已经加入到生成树中,所以对应的lowCost值无需修改(因为之后不会再加入v0、v3、v2和v5这四个顶点),
最终lowCost数组中的值依次为0、5、4、1、6、2,
如下图:

如下图,开始进行第四轮处理:

首先需要检查isJoin数组和lowCost数组,最终找出一个还没有被加入生成树且代价最低的顶点,
由上述图片可知,v1顶点没有加入生成树中且代价最小,因此把v1顶点加入生成树中,如下图:

如上图,要把v1顶点在isJoin数组中对应的值修改为true即勾,表示已加入生成树中,继续如下图:

如上图,需要循环遍历lowCost数组,更新还没加入的各个顶点对应的lowCost值,
由上述图片可知,加入v1顶点之后,
加入v4的最小代价为3,因此把v4对应的lowCost值修改为2,
由于v0、v3、v2、v5和v1这五个顶点已经加入到生成树中,所以对应的lowCost值无需修改(因为之后不会再加入v0、v3、v2、v5和v1这五个顶点),
最终lowCost数组中的值依次为0、5、4、1、3、2,

如下图,开始进行第五轮处理:

首先需要检查isJoin数组和lowCost数组,最终找出一个还没有被加入生成树且代价最低的顶点,
由上述图片可知,v4顶点没有加入生成树中且代价最小,因此把v4顶点加入生成树中,如下图:

如上图,要把v4顶点在isJoin数组中对应的值修改为true即勾,表示已加入生成树中,
最终所有顶点全部加入到生成树中,Prim算法结束。
2.时间复杂度分析:

上述例子中进行了好几轮的处理最终得出最小生成树,从代码角度来看就是好几轮的循环,
由于每一轮的循环都会选择一个新的顶点把它放入生成树中,假设图中有n个顶点就需要n-1轮的循环,因为第一个顶点不需要循环,
而每一轮的处理当中又需要进行两次循环遍历,第一次循环遍历所有的顶点来从isJoin数组和lowCost数组中找出未加入生成树且代价最小的顶点,第二次循环遍历所有的顶点来更新lowCost数组,所以每一轮的时间复杂度为O(2n),等价于O(n),
由于需要n-1轮循环,所以总的时间复杂度就是O( n * (n-1) ),等价于O( n * n - n ),等价于O( n * n ),
如果改为图中有V个顶点,时间复杂度就是O( |V| * |V|)。
七.Kruskal算法(克鲁斯卡尔)的实现思想:
1.实例:
如下图,由于Kruskal算法(克鲁斯卡尔)每次要选择一条权值最小的边,所以要先把各条边按照权值递增的次序进行排序:

如上图,权值最小的边是权值为1的这条边,两边的顶点是v0和v3,所以上述图片里的第一行数据中weight为1、Vertex1为v0、Vertex2为v3,该算法的执行过程就是把所有的边都检查一遍。

如上图,第一条边的权值为1,两边连的顶点是v0和v3,接下来就要检查v0和v3是否连通,进行这个判断用到了并查集(详情见"5.15.并查集"),大致的思想就是刚开始要把所有的顶点分别看作是不同的集合,所以对于第一条边的两个顶点v0和v3,他们刚开始从属于不同集合,也就意味着他们此时不连通,因此就可以把这条边选中,如下图:

此时v0和v3这两个顶点就属于同一个集合了,
如下图,接下来进行第二轮的处理,权值为2的边的两头为v2和v5,v2和v5此时不属于同一个集合即v2和v5不连通,所以把v2和v5连起来,把v2和v5归并为同一个集合:

如下图,接下来进行第三轮的处理,权值为3的边的两头为v1和v4,v1和v4此时不属于同一个集合即v1和v4不连通,所以把v1和v4连起来,把v1和v4归并为同一个集合:

如下图,接下来进行第四轮的处理,其中一条权值为4的边的两头为v2和v3,v2和v3此时不属于同一个集合即v2和v3不连通,所以把v2和v3连起来,把v2和v3归并为同一个集合:

如下图,接下来进行第五轮的处理,其中一条权值为4的边的两头为v3和v5,v3和v5此时属于同一个集合即v3和v5连通,所以v3和v5之间的边会跳过,不选中:

接下来的过程同理,最终把v1与v3连接后就得出最小生成树,
如下图,总之就是要把所有的边都遍历一遍,每当处理一条边时,需要判断这条边所连接的两个顶点是否从属于同一个集合,如果不是,那就把这条边选中,如果是,就不选中:

2.时间复杂度分析:
假设图中共有e条边:

每轮循环中判断两个顶点是否属于同一个集合,要用到并查集,这个过程的时间复杂度详情见"5.15.并查集",共e轮。
八.总结:

相关文章:

6.8.最小生成树
一.复习: 1.生成树: 对于一个连通的无向图,假设图中有n个顶点,如果能找到一个符合以下要求的子图: 子图中包含图中所有的顶点,同时各个顶点保持连通, 而且子图的边的数量只有n-1条࿰…...

MATLAB 控制系统设计与仿真 - 37
范数鲁棒控制器的设计 鲁棒控制器的设计 根据双端子状态方程对象模型结构,控制器设计的目标是找到一个控制器K(s),它能保证闭环系统的范数限制在一个给定的小整数下,即 这时控制器的状态方程为: 其中X与Y分别为下面两个代数Riccati方程的解…...

社交媒体时代的隐私忧虑:聚焦Facebook
在数字化时代,社交媒体平台已成为人们日常生活的重要组成部分。Facebook作为全球最大的社交媒体之一,拥有数十亿用户,其对个人隐私的影响和忧虑也日益凸显。本文将探讨社交媒体时代下,尤其是Facebook平台上的隐私问题。 数据收集…...

9.Rust+Axum 测试驱动开发与性能优化全攻略
摘要 本文深入讲解 RustAxum 测试驱动开发及性能优化,涵盖多种测试工具与优化技术。 一、引言 在当今的软件开发领域,测试驱动开发(TDD)和性能优化是保障软件质量和性能的关键环节。Rust 作为一种安全、高效的系统编程语言&…...
)
中国首个全国34省3,667个城市多属性建筑数据集(屋顶、高度、结构、功能、风格、年龄、质量等属性)
中国首个全国34省3,667个城市多属性建筑数据集(屋顶、高度、结构、功能、风格、年龄、质量等属性) 数据介绍 快速获取三维(3D)建筑数据,包括屋顶、高度和方向等几何属性,以及功能、质量和年龄等指示性属性…...

探索Spring Boot Web模块:设计思想与技术实现
探索Spring Boot Web模块:设计思想与技术实现 在现代Web开发中,Spring Boot作为一个强大的框架,提供了丰富的功能来简化Web应用的开发。本文将深入探讨Spring Boot框架中Web模块的核心类,揭示其设计思想、技术实现以及扩展知识。…...

GitHub创建远程仓库
使用GitHub创建远程仓库:从零开始实现代码托管与协作 前言 在当今软件开发领域,版本控制系统已成为开发者必备的核心工具。作为分布式版本控制系统的代表,Git凭借其强大的分支管理和高效的协作能力,已成为行业标准。而GitHub作为…...

PLM系统如何支持利益相关者分析?沟通矩阵设计
PLM(产品生命周期管理)系统在现代企业的产品研发与管理过程中扮演着至关重要的角色。它不仅仅是一个管理产品数据的工具,更能在利益相关者分析以及沟通矩阵设计方面提供强大的支持。通过合理运用PLM系统,企业能够更好地识别、理解…...
 求解矩阵最小路径和问题)
每日一题(8) 求解矩阵最小路径和问题
给定一个m行n列的矩阵,从左上角开始每次只能向右或者向下移动,最后到达右下角的位置,路径上的所有数字累加起来作为这条路径的路径和。求所有路径和中最小路径和。 输入格式: 首先输入行数m及列数n,接下来输入m行,每…...

JAVA设计模式:注解+模板+接口
1.基础组件 1.1注解类控制代码执行启动、停止、顺序 /*** author : test* description : 数据同步注解* date : 2025/4/18*/ Target({ElementType.TYPE}) Retention(RetentionPolicy.RUNTIME) Documented public interface SyncMeta {/*** 执行服务名称* return*/String name…...

如何在Linux系统中部署C++ Web应用
在 Linux 上部署 C Web 应用,和部署传统的 PHP 或 Node.js 应用相比更“原生”一些,通常涉及到自己编译、配置 Web 服务、处理依赖等。本文将详细讲解部署一个基于 C 编写的 Web 应用的完整流程,涵盖从构建、部署、到上线的每一步,…...
)
实用工具-screenrec介绍(截图工具)
官方地址:Communicate Faster with Instant Video Messages & Screenshots 官方下载安装包,安装完成后,默认快捷键 alt s 开启截图,录屏 介绍 ScreenRec 是一款免费无广告的屏幕录制与截图工具,支持多平台&…...

使用veaury,在vue项目中运行react组件
网上的信息太少了,记录一下 我的项目是vue3webpack 使用:veaury Veaury 是基于React和Vue3的工具库,主要用于React和Vue在一个项目中公共使用的场景,主要运用在项目迁移、技术栈融合的开发模式、跨技术栈使用第三方组件的场景。 参…...

开源 vs. 闭源:大模型的未来竞争格局
开源 vs. 闭源:大模型的未来竞争格局 引言 在人工智能领域,尤其是大型语言模型(LLM)的发展中,开源与闭源之争已成为决定行业未来走向的关键议题。随着ChatGPT的横空出世和开源模型的蓬勃发展,技术社区正经历着一场深刻的范式转变…...

pcl代码解析
一、库基础代码解析: PCL库基础:点云类型与算法详解-CSDN博客 主要介绍PCL库的一些基本的点云类型、相关数据类型以及ROS接口消息,和一些常用的算法。 用到的一些PCL点云类型 pcl::PointXYZ: 这是最简单也可能是最常用到的点类型;它只储存…...

中华传承-医山命相卜-梅花易数
梅花易数 灵活起卦(如数字、声音、外应等)和象数结合,准确率可达96.8%。其起卦方式摆脱传统龟壳、蓍草的繁琐,强调直觉与灵活性。 个人决策、事件预测等 尤其在短期、具体问题上表现突出。...

HOOPS Exchange 与HOOPS Communicator集成:打造工业3D可视化新标杆!
一、概述 在工业3D开发、BIM建筑、数字孪生和仿真分析等高端应用场景中,数据格式复杂、模型体量庞大、实时交互体验要求高,一直是困扰开发者的难题。Tech Soft 3D旗下的HOOPS Exchange和HOOPS Communicator,正是解决这类问题的黄金搭档。二者…...

SQL预编译——预编译真的能完美防御SQL注入吗
SQL注入原理 sql注入是指攻击者拼接恶意SQL语句到接受外部参数的动态SQL查询中,程序本身 未对插入的SQL语句进行过滤,导致SQL语句直接被服务端执行。 拼接的SQL查询例如,通过在id变量后插入or 11这样的条件,来绕过身份验证&#…...
自定义文献引用和参考文献列表的格式)
通过 Zotero 的样式编辑器(Style Editor)自定义文献引用和参考文献列表的格式
好的!以下是一个更为详细的教程,帮助你通过 Zotero 的样式编辑器(Style Editor)自定义文献引用和参考文献列表的格式。 详细教程:使用 Zotero 样式编辑器自定义文献格式 1. 准备工作 在开始之前,请确保&a…...
 导入几何数据)
PostgreSQL 通过 copy 命令导入几何数据 及 通过 CopyManager.copyIn() 导入几何数据
COPY命令介绍 copy是postgresql提供的一个专门用于快速导入导出数据的命令,通常用于从文件(TXT、CSV等)或标准输入输出中读取或写入数据。适合批量导入导出数据,速度快。 默认情况下,如果在处理过程中遇到错误,COPY将失败。 COPY只能用于表,不能用于视图!!! COPY…...

Next.js 技术详解:构建现代化 Web 应用的全栈框架
1. Next.js 概述 Next.js 是一个基于 React 的全栈框架,由 Vercel 团队开发和维护。它提供了一系列开箱即用的功能,使开发者能够快速构建高性能的 Web 应用。 核心优势 服务端渲染 (SSR)静态站点生成 (SSG)增量静态再生成 (ISR)文件系统路由API 路由图…...
的Sync同步和Timing定时参数使用介绍,同步动画层制作角色的受伤状态)
【unity实战】Unity动画层级(Animation Layer)的Sync同步和Timing定时参数使用介绍,同步动画层制作角色的受伤状态
文章目录 前言方案一:复制粘贴原有层级的状态机1、实现2、问题 方法二:勾选Sync同步动画层1、简单实现同步2、同步blend tree的问题3、动画状态的播放时长4、下层状态覆盖了上层状态 专栏推荐完结 前言 如何制作角色的受伤状态? 玩家角色在…...

NFC 碰一碰发视频源码搭建,碰一碰发视频定制化开发技术
在移动互联时代,便捷的数据传输方式备受青睐。NFC(近场通信)技术以其操作简单、连接迅速的特性,为设备间的数据交互提供了高效解决方案。通过搭建 NFC 碰一碰发视频功能,用户只需将支持 NFC 的设备轻轻靠近,…...

获取视频封面
目录 实现方式注意事项代码实现 实现方式 通过 video 元素canvas 元素的方式实现 生成 video 和 canvas 元素当 video 元素资源加载完成时,将 video 元素绘制到 canvas 画布上,然后通过 toBlob 或则 toDataURL 获取到对应的封面图片资源 注意事项 vid…...

c#开发大冲锋游戏登录器
1 前言 本文主要分享登录器的简要开发过程,只适合小白选手,高手请自动避让。 此项目是复刻大冲锋计划中的子集。 (注:大冲锋是迅雷代理的一款次时代多职业第一人称FPS射击游戏,目前已经关服嗝屁。) 2 …...

堆的实现以及利用堆进行排序
堆 堆的实现1. 什么是堆?2. 最小堆的核心操作2.1 初始化堆2.2 销毁堆2.3 插入元素2.4 删除堆顶元素2.5 获取堆顶元素2.6 判断堆是否为空 3. 调整堆的算法3.1 向上调整3.2 向下调整 4. 测试代码 堆排序一.向下调整建堆二.向上调整建堆 时间复杂度分析向上建堆分析&am…...

FPGA-VGA
目录 前言 一、VGA是什么? 二、物理接口 三、VGA显示原理 四、VGA时序标准 五、VGA显示参数 六、模块设计 七、波形图设计 八、彩条波形数据 前言 VGA的FPGA驱动 一、VGA是什么? VGA(Video Graphics Array)是IBM于1987年推出的…...

仿腾讯会议项目开发——界面关闭功能实现
目录 1、include(./netapi/netapi.pri) 2、加快构建速度 3、INCLUDEPATH./netapi 4、添加控制类 5、用单例模式创建一个Ckernel的对象 6、创建一个回收的槽函数 7、添加界面文件 8、创建一个私有的界面对象 9、修改为使用单例模式的控制类创建界面 10、在Ckernel类中…...
)
微信小程序怎么分包步骤(包括怎么主包跳转到分包)
第一步 主包跳转到分包 第一步 第二步...

点云配准控制迭代停止的阈值
在点云配准(如ICP算法)中,setEuclideanFitnessEpsilon() 是一个设置收敛条件的函数,用于控制迭代停止的阈值。以下是关于该参数的详细说明: 函数作用 setEuclideanFitnessEpsilon() 设置的是 两次连续迭代之间均方误…...

高频面试题:Android MVP/MVVM/MVI这几种架构在实际生产中,各自的优缺点和适用场景是什么
安卓开发早期的架构模式相对简单,许多开发者直接在Activity或Fragment中堆砌业务逻辑和UI操作,这种方式虽然在小型项目中看似高效,但随着代码量的增加,很快就会导致逻辑混乱、难以测试和维护的问题。Activity和Fragment作为安卓框…...

国内主要半导体厂家
以下是国内主要半导体厂家按产品类别(模拟、数字、MCU、功率、传感器等)的分类总结,涵盖各领域代表企业及其核心产品方向: 一、模拟芯片(Analog IC) 圣邦微电子(SGMICRO)…...

DeepSeek深度观察:白宫“炒人“威胁的语义强度与市场应激量化分析
一、AI观察:政治博弈的语义强度分析 通过NLP情感分析模型对特朗普近期公开言论的语义解析显示,总统在社交媒体及记者会中多次使用"立即解雇""卷铺盖走人"等极端表述,其公开威胁解雇鲍威尔的推文互动量突破120万次&#…...

城市街拍暗色电影胶片风格Lr调色教程,手机滤镜PS+Lightroom预设下载!
调色介绍 城市街拍暗色电影胶片风格 Lr 调色,是借助 Adobe Lightroom 软件,为城市街拍的人像或场景照片赋予独特视觉风格的后期处理方式。旨在模拟电影胶片质感,营造出充满故事感与艺术感的暗色氛围,让照片仿佛截取于某部充满张力…...

图像分类标注小工具
图像分类标注小工具 不说废话 上代码 import os import cv2 import shutil import csvclass ImageLabeler:def __init__(self, input_dir, output_dir, class_names, csv_pathlabel_log.csv, preview_size(800, 800)):self.input_dir input_dirself.output_dir output_dirse…...

leetcode 2364. 统计坏数对的数目 中等
给你一个下标从 0 开始的整数数组 nums 。如果 i < j 且 j - i ! nums[j] - nums[i] ,那么我们称 (i, j) 是一个 坏数对 。 请你返回 nums 中 坏数对 的总数目。 示例 1: 输入:nums [4,1,3,3] 输出:5 解释:数对…...

网络互连与互联网3
1.SMTP简单邮件传输协议,用于发送电子邮件,默认情况下是明文传输,没有加密机制。 SSL是一种安全协议,对电子邮件进行加密传输。 POP3主要用于接收电子邮件 IMAP用于接收电子邮件 2.采用存储-转发方式处理信号的设备是交换机 …...
项目)
docker部署springboot(eureka server)项目
打jar包 使用maven: <build><plugins><plugin><groupId>org.apache.maven.plugins</groupId><artifactId>maven-compiler-plugin</artifactId><configuration><source>17</source><target>17&…...

git 出现 port 443 Connection timed out
梯子正常延迟不算严重,但在使用git push时反复出现 fatal: unable to access https://github.com/irvingwu5/xxxx.git/ Error in the HTTP2 framing layer Failed to connect to github.com port 443 after 136353 ms: Connection timed out 将git的网络配置与梯子…...

深入 MySQL 高级查询:JOIN、子查询与窗口函数的实用指南
在数据管理和分析的过程中,MySQL 提供了强大的查询功能,特别是在处理复杂数据关系时。本文将深入探讨 MySQL 的三种高级查询技术:JOIN、子查询和窗口函数。通过对这些技术的详细讲解和示例,帮助您更好地掌握并应用这些查询技巧。 …...

AXOP36061S: 60V 高压单通道运算放大器
AXOP36061S 是一款通用型高压带关断功能的单通道运算放大器,工作电压为3V至60V,具有17MHz的带宽和 15V/μs的压摆率,静态电流2.2mA,关断电流80μA,高耐压和宽带宽使其可以胜任绝大多数的高压应用场景。得益于对噪声和T…...

Aladdin显卡多任务运行教程
Aladdin显卡多任务运行 任务场景操作步骤其他说明 任务场景 当我运行我的代码后发现80G的显存仅占用了46G左右,还有很大空间没有被使用,于是想着能不能把剩下的空间也利用起来,于是有了接下来的工作。 操作步骤 当我们使用GPU run/debug/…...

Oracle AWR快照保留策略及其修改
文章目录 一、AWR快照保留机制及其修改方法二、生产环境建议三、监控建议 一、AWR快照保留机制及其修改方法 默认保留策略: • 标准保留期:8天 • 快照间隔:每小时1次(默认) • 存储位置:SYSAUX表空间 保留…...

日本公司如何实现B2B商城订货系统的自动化和个性化?
在日本构建具备前后台日文本地化、业务员代客下单、一客一价、智能拆单发货的B2B电商系统,需结合日本商业习惯与技术实现。以下是关键模块的落地方案: 一、系统架构设计 1. 前端本地化 语言与UI适配 采用全日语界面,包含敬语体系(…...

JavaScript 核心特性完全指南
引言 JavaScript 已经不再只是浏览器中的脚本语言,它支撑着前端、后端(Node.js)、桌面(Electron)、移动端(React Native)等多种生态。要在现代 Web 开发中游刃有余,除了会写代码,更要深刻理解语言特性、掌握常见模式和优化技巧。下面逐一深入解析 20 大核心特性。 1.…...

CentOS系统中排查进程异常终止的日志
在CentOS系统中排查进程异常终止的日志,可通过以下步骤结合多类日志文件和工具进行综合分析: 一、核心日志文件排查 系统全局日志 查看 /var/log/messages:记录系统级错误、内核消息及进程异常终止信息,如OOM Killer事件。…...

Vue组件安全工程的量子跃迁:从基因改造到生态免疫
总章数字生命的进化论 2023年某电商平台红蓝对抗中,一个未净化的v-html指令导致千万用户数据泄露。当我们剖开现代Web应用的器官式架构,发现90%的安全漏洞都源自组件间的信任危机。本文将带您见证如何用军工级防御体系重构Vue组件,使其具备类…...

编程技能:调试03,逐过程命令与退出调试
专栏导航 本节文章分别属于《Win32 学习笔记》和《MFC 学习笔记》两个专栏,故划分为两个专栏导航。读者可以自行选择前往哪个专栏。 (一)WIn32 专栏导航 上一篇:编程技能:调试02,设置断点与删除断点 回…...

基于Ubuntu22.04和OpenCV4.5.4的物联网人脸识别考勤机
前言:本人已有Ubuntu22.04的相关开发环境配置,并且默认C和机器学习基础,这里直接从安装opencv开始,完整代码在最后。具体情况具体分析,请以实际为主。 视频参考:【大厂敲门砖】从0到1做一个物联网人脸识别…...

java 排序算法-快速排序
快速排序(Quick Sort)是一种高效的排序算法,它使用分治法(Divide and Conquer)策略来把一个序列分为较小和较大的两个子序列,然后递归地排序两个子序列。 快速排序算法的基本思想: 选择基准值&…...
