数据结构-树（1）

一、树的基本概念

二，树的抽象数据结构

三，树的存储结构

1.双亲表示法

• 数组存储结点，含数据域和双亲下标（根结点双亲为 - 1）
• 
• 
• 

代码示例

• include <stdio.h>
  #include <stdlib.h>#define MAX_TREE_SIZE 100
  typedef int TElemType;// 双亲表示法结点结构
  typedef struct PTNode {TElemType data;        // 结点数据int parent;           // 双亲位置下标（-1表示无双亲）
  } PTNode;// 树结构
  typedef struct {PTNode nodes[MAX_TREE_SIZE];  // 结点数组int r, n;                   // 根的位置和结点数
  } PTree;// 初始化树（示例：构建文档中的树结构）
  void InitTree(PTree* T) {TElemType data[] = { 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J' };T->n = 10;T->r = 0;  // 根结点下标为0// 设定各结点的双亲T->nodes[0].data = data[0];T->nodes[0].parent = -1;T->nodes[1].data = data[1];T->nodes[1].parent = 0;T->nodes[2].data = data[2];T->nodes[2].parent = 0;T->nodes[3].data = data[3];T->nodes[3].parent = 1;T->nodes[4].data = data[4];T->nodes[4].parent = 2;T->nodes[5].data = data[5];T->nodes[5].parent = 2;T->nodes[6].data = data[6];T->nodes[6].parent = 3;T->nodes[7].data = data[7];T->nodes[7].parent = 3;T->nodes[8].data = data[8];T->nodes[8].parent = 3;T->nodes[9].data = data[9];T->nodes[9].parent = 4;
  }// 输出每个结点的双亲
  void PrintParents(PTree T) {printf("结点\tdata\tparent\n");for (int i = 0; i < T.n; i++) {printf("%d\t%c\t%d\n", i, T.nodes[i].data, T.nodes[i].parent);}
  }int main() {PTree T;InitTree(&T);printf("双亲表示法存储结构:\n");PrintParents(T);return 0;
  }

  

2.孩子表示法

每个结点有多个指针域，其中每个指针指向一颗子树的根结点，我们把这种方法叫做多重链表表示法

有两种方案解决

方案一：

一种是指针域的个数就等于树的度，树的度是树各个结点度的最大值

这种方法对于树中的各个结点的度相差很大时，显然是很浪费空间的，因为有很多的结点，它的指针域是空的。

不过如果树的各结点度相差很小时，那就意味着开辟的空间被充分利用了，这时存储结构的缺点反而变成了优点

方案二

第二种方案每个结点指针域的个数等于该结点的度，我们专门取一个位置来存储结点指针域的个数

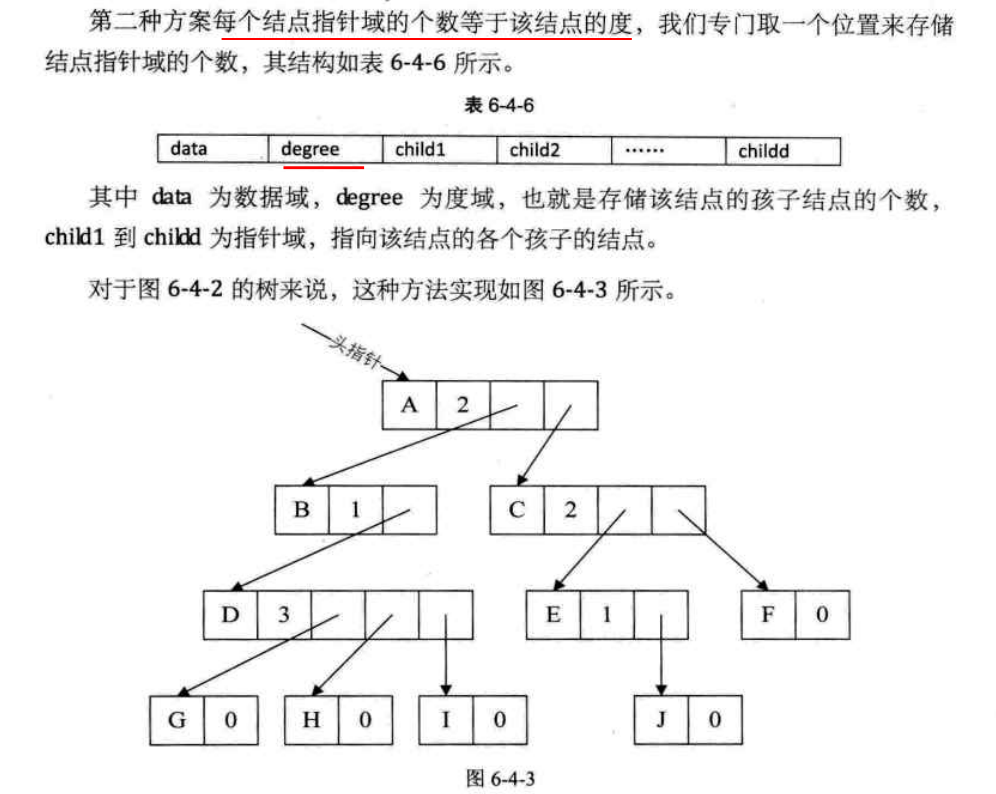
这种方法克服了浪费空间的缺点，对空间利用率是很高的，但是由于各个结点的链表是不相同的结构，加上要维护结点的度的 数值，在运算上就会带来时间上的损耗

这时，我们想到了更好的办法，既可以减少空指针的浪费又能使结点结构相同

这就是孩子表示法，具体办法就是，把每个结点的孩子结点排列起来，以单链表作存储结构，则n个结点有n个孩子链表，如果是叶子结点则此单链表为空；然后n个指针又组成一个线性表，采用顺序存储结构，存放进一个一维数组中

/*树的孩子表示法的结构定义代码*/
#define MAX_TREE_SIZE 100
typedef struct CTNode //孩子结点
{int child;struct CTNode *next;
}*ChildPtr;typedef struct //表头结构
{TElemType data;ChildPtr firstchild;
}*CTBox;typedef struct
{CTBox nodes[MAX_TREE_SIZ];int r,n;
}CTree;

代码示例：

#include <stdio.h>
#include <stdlib.h>#define MAX_TREE_SIZE 100
typedef char TElemType; // 修改为char类型以匹配数据初始化// 孩子结点
typedef struct CTNode {int child;          // 孩子结点下标struct CTNode* next; // 指向下一个孩子的指针
} *ChildPtr;// 表头结构
typedef struct CTBox {TElemType data;      // 结点数据ChildPtr firstchild; // 第一个孩子指针
} CTBox;// 树结构
typedef struct {CTBox nodes[MAX_TREE_SIZE];  // 表头数组int r, n;                   // 根的位置和结点数
} CTree;// 创建新的孩子结点
ChildPtr createChildNode(int childIndex) 
{ChildPtr newNode = (ChildPtr)malloc(sizeof(struct CTNode));if (newNode == NULL) {printf("内存分配失败\n");exit(EXIT_FAILURE);}newNode->child = childIndex;newNode->next = NULL;return newNode;
}// 添加孩子结点到指定父结点
void addChild(CTree* T, int parentIndex, int childIndex)
{ChildPtr newNode = createChildNode(childIndex);newNode->next = T->nodes[parentIndex].firstchild;T->nodes[parentIndex].firstchild = newNode;
}// 创建完整的树结构（示例：构建书中图6-4-1的树）
void CreateChildTree(CTree* T) 
{TElemType data[] = { 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J' };T->n = 10;T->r = 0;  // 根结点下标为0// 初始化表头数据for (int i = 0; i < T->n; i++) {T->nodes[i].data = data[i];T->nodes[i].firstchild = NULL;}// 添加所有孩子结点关系addChild(T, 0, 1); // A的孩子: BaddChild(T, 0, 2); // A的孩子: CaddChild(T, 1, 3); // B的孩子: DaddChild(T, 2, 4); // C的孩子: EaddChild(T, 2, 5); // C的孩子: FaddChild(T, 3, 6); // D的孩子: GaddChild(T, 3, 7); // D的孩子: HaddChild(T, 3, 8); // D的孩子: IaddChild(T, 4, 9); // E的孩子: J
}// 输出每个结点的孩子列表
void PrintChildren(CTree T) 
{printf("结点\tdata\t孩子列表\n");for (int i = 0; i < T.n; i++) {printf("%d\t%c\t", i, T.nodes[i].data);ChildPtr p = T.nodes[i].firstchild;while (p) {printf("%d(%c) ", p->child, T.nodes[p->child].data);p = p->next;}printf("\n");}
}// 释放树的内存
void destroyTree(CTree* T) 
{for (int i = 0; i < T->n; i++) {ChildPtr current = T->nodes[i].firstchild;while (current != NULL) {ChildPtr next = current->next;free(current);current = next;}}
}int main() {CTree T;CreateChildTree(&T);printf("孩子表示法存储结构:\n");PrintChildren(T);destroyTree(&T); // 释放内存return 0;
}

这时，也存在着问题，我如何知道某个结点的双亲是谁呢？比较麻烦，需要整棵树遍历才行。

我们可以把双亲表示法和孩子表示法综合一下。

 

代码示例：

#include <stdio.h>
#include <stdlib.h>#define MAX_TREE_SIZE 100
typedef char TElemType; // 结点数据类型（示例为字符型）// 孩子结点结构（用于孩子链表）
typedef struct ChildNode 
{int child_idx;       // 孩子结点在数组中的下标struct ChildNode* next; // 指向下一个兄弟结点
} ChildNode;// 双亲孩子表示法的结点结构
typedef struct PTNode 
{TElemType data;           // 结点数据int parent_idx;          // 双亲结点下标（-1表示根结点）ChildNode* first_child;  // 第一个孩子结点指针
} PTNode;// 树结构
typedef struct 
{PTNode nodes[MAX_TREE_SIZE]; // 结点数组int root_idx;                // 根结点下标int node_count;              // 结点总数
} ParentChildTree;// 创建孩子结点
ChildNode* create_child_node(int child_idx) 
{ChildNode* node = (ChildNode*)malloc(sizeof(ChildNode));node->child_idx = child_idx;node->next = NULL;return node;
}// 向双亲孩子结点中添加孩子
void add_child(ParentChildTree* tree, int parent_idx, int child_idx) 
{ChildNode* new_node = create_child_node(child_idx);// 将新孩子插入到孩子链表头部（或尾部，此处示例为头部）new_node->next = tree->nodes[parent_idx].first_child;tree->nodes[parent_idx].first_child = new_node;// 设置孩子的双亲tree->nodes[child_idx].parent_idx = parent_idx;
}// 初始化示例树（构建书中图6-4-1的树结构）
void init_example_tree(ParentChildTree* tree) 
{// 初始化结点数据TElemType data[] = { 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J' };tree->node_count = 10;tree->root_idx = 0; // 根结点下标为0// 初始化每个结点的基本信息（无孩子和双亲）for (int i = 0; i < tree->node_count; i++) {tree->nodes[i].data = data[i];tree->nodes[i].parent_idx = -1;tree->nodes[i].first_child = NULL;}// 添加孩子关系（按书中示例树结构）// A的孩子：B（下标1）、C（下标2）add_child(tree, 0, 1);add_child(tree, 0, 2);// B的孩子：D（下标3）add_child(tree, 1, 3);// C的孩子：E（下标4）、F（下标5）add_child(tree, 2, 4);add_child(tree, 2, 5);// D的孩子：G（下标6）、H（下标7）、I（下标8）add_child(tree, 3, 6);add_child(tree, 3, 7);add_child(tree, 3, 8);// E的孩子：J（下标9）add_child(tree, 4, 9);
}// 打印树的存储结构
void print_tree(ParentChildTree tree) 
{printf("结点\t数据\t双亲\t孩子列表\n");for (int i = 0; i < tree.node_count; i++) {PTNode node = tree.nodes[i];printf("%d\t%c\t", i, node.data);printf("%d\t", node.parent_idx);// 打印孩子列表ChildNode* child = node.first_child;printf("孩子: ");while (child) {printf("%d ", child->child_idx);child = child->next;}printf("\n");}
}// 释放内存（避免内存泄漏）
void free_tree(ParentChildTree* tree) 
{for (int i = 0; i < tree->node_count; i++) {ChildNode* child = tree->nodes[i].first_child;while (child) {ChildNode* temp = child;child = child->next;free(temp);}}
}int main() {ParentChildTree tree;init_example_tree(&tree);printf("双亲孩子表示法存储结构:\n");print_tree(tree);free_tree(&tree); // 释放内存return 0;
}

3.孩子兄弟表示法

任一棵树，它的结点的第一个孩子如果存在就是唯一的，它的右兄弟如果存在也是唯一的。因此，我们设置两个指针，分别指向该结点的第一个孩子和此结点的右兄弟

                                

其中 data 是数据域，frstchikd 为指针域，存储该结点的第一个孩子结点的存储地址，rightsib是指针域，存储该结点的右兄弟结点的存储地址。

/*树的孩子兄弟表示法结构定义*/
typedef struct CSNode
TElemType datar
struct CsNode *firstchild,*rightsib;CSNode,*CsTreei

代码示例：

#include <stdio.h>
#include <stdlib.h>typedef int TElemType;// 孩子兄弟表示法结点结构
typedef struct CSNode {TElemType data;struct CSNode* firstchild, * rightsib;
} CSNode, * CSTree;// 创建示例树（简单二叉树结构）
CSTree CreateCSTree() {// 手动构建示例树（根结点A，左孩子B，右孩子C）CSNode* A = (CSNode*)malloc(sizeof(CSNode));CSNode* B = (CSNode*)malloc(sizeof(CSNode));CSNode* C = (CSNode*)malloc(sizeof(CSNode));A->data = 'A';A->firstchild = B;A->rightsib = NULL;B->data = 'B';B->firstchild = NULL;B->rightsib = C;C->data = 'C';C->firstchild = NULL;C->rightsib = NULL;return A;
}// 前序遍历孩子兄弟表示法的树
void PreOrder(CSTree T) {if (T) {printf("%c ", T->data);PreOrder(T->firstchild);  // 遍历长子PreOrder(T->rightsib);    // 遍历右兄弟}
}int main() {CSTree T = CreateCSTree();printf("孩子兄弟表示法遍历结果:\n");PreOrder(T);  // 输出: A B Creturn 0;
}

如果有必要，可以再增加一个parent指针域来解决快速查找双亲的问题

代码如下：

#include <stdio.h>
#include <stdlib.h>typedef int TElemType;// 孩子兄弟表示法结点结构，增加parent指针域
typedef struct CSNode {TElemType data;struct CSNode* firstchild, * rightsib;struct CSNode* parent; // 新增parent指针，指向父结点
} CSNode, * CSTree;// 创建示例树（简单二叉树结构）
CSTree CreateCSTree() {// 手动构建示例树（根结点A，左孩子B，右孩子C）CSNode* A = (CSNode*)malloc(sizeof(CSNode));CSNode* B = (CSNode*)malloc(sizeof(CSNode));CSNode* C = (CSNode*)malloc(sizeof(CSNode));A->data = 'A';A->firstchild = B;A->rightsib = NULL;A->parent = NULL; // 根结点的parent为NULLB->data = 'B';B->firstchild = NULL;B->rightsib = C;B->parent = A; // B的父结点是AC->data = 'C';C->firstchild = NULL;C->rightsib = NULL;C->parent = A; // C的父结点是Areturn A;
}// 前序遍历孩子兄弟表示法的树
void PreOrder(CSTree T) {if (T) {printf("%c ", T->data);PreOrder(T->firstchild);  // 遍历长子PreOrder(T->rightsib);    // 遍历右兄弟}
}// 通过parent指针查找指定结点的双亲
CSNode* FindParent(CSTree T, TElemType target) {if (T == NULL) {return NULL;}if (T->data == target) {return T->parent;}CSNode* temp = T->firstchild;while (temp) {CSNode* parent = FindParent(temp, target);if (parent) {return parent;}temp = temp->rightsib;}return NULL;
}int main() {CSTree T = CreateCSTree();printf("孩子兄弟表示法遍历结果:\n");PreOrder(T);  // 输出: A B Cprintf("\n");TElemType target = 'B';CSNode* parent = FindParent(T, target);if (parent) {printf("结点%c的双亲是%c\n", target, parent->data);}else {printf("未找到结点%c的双亲\n", target);}return 0;
}